Презентация на тему: «Теория вероятности» 9 класс

Теория вероятностей в современном мире Выполнили: Лихобабина Анастасия, Кулыгина Анастасия, 9 “А” класс Научный руководитель: Черная Марина Михайловна 5klass.net

Оглавление: Историческая справка. С чего начиналась теория вероятностей? Задача де Мере. Основные понятия теории вероятностей. Случайные величины. Закон распределения. Пример. Теория вероятностей в современном мире. Химия & математика. Применение в статистике. Физика & математика. Применение в астрономии. Применение в сельском хозяйстве. Применение в медицине. Применение в промышленности. Применение в азартных играх (рулетка). Применение в логических играх. Список использованной литературы и сайтов.

Историческая справка

С чего начиналась теория вероятностей? Теория вероятностей, как наука, зародилась в середине XVII века в романтическое время. Вероятностные закономерности впервые были обнаружены в азартных играх, когда начали применять в них количественные подсчеты и прогнозировать шансы на успех.

Задачи де Мере Шевалье (кавалер) де Мере (1607-1648), придворный французского короля, азартный игрок.

Сколько раз надо бросить две игральные кости, чтобы случаев выпадения пары шестерок было больше, чем случаев невыпадения пары шестерок? Как справедливо разделить поставленные на кон деньги, если игроки прекратили игру преждевременно?

Пьер де Ферма (1601-1665)

Задача де Мере Де Мере держал пари, что при четырех подбрасываниях игральной кости выпадет, по крайней мере, одна шестерка. Решение: 64=1296 – общее число исходов. 64 - 54=671 – шансы появления хотя бы одной шестерки. 54=625 – случаи невыпадения шестерки. Так как 671>625, то при 4 бросаниях выгоднее сделать ставку на то, что выпадет хотя бы одна шестерка.

Введем следующие понятия: Теория вероятностей — раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.

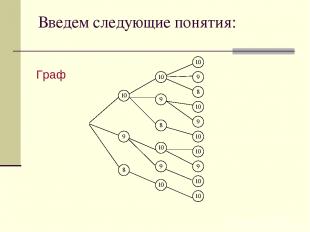
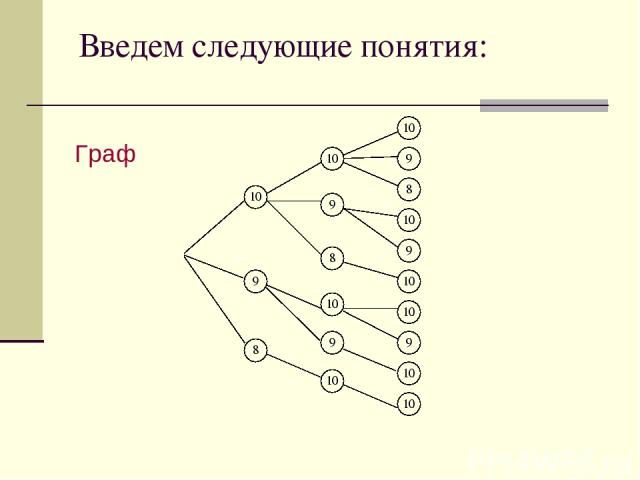
Введем следующие понятия: Граф

Введем следующие понятия: Испытание Единичное испытание Исходы испытания Случайные исходы испытания Множество исходов испытания

Введем следующие понятия: Связный граф Цикл Дерево Случайное событие Вероятность случайного события

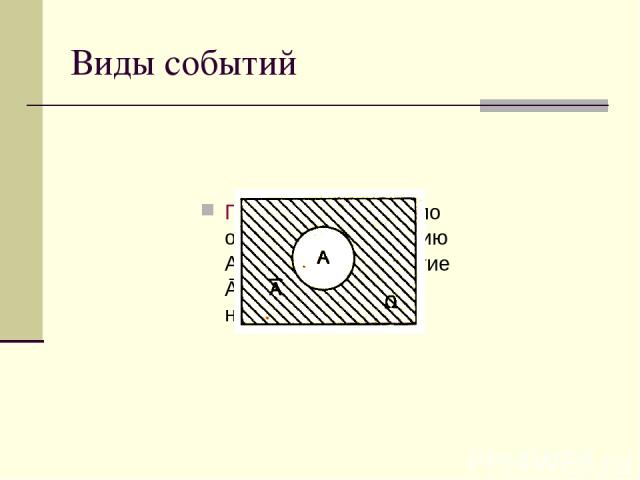
Виды событий Невозможное событие Достоверное событие

Виды событий Суммой двух событий А и В называется событие С=А+В, состоящее в выполнении события А или события В. Произведением двух событий А и В называют событие, состоящее в совместном появлении этих событий D=А•В

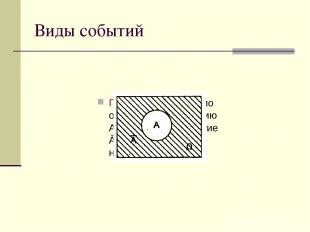
Виды событий Противоположным по отношению к событию А называется событие Ā, состоящее в непоявлении А.

Виды событий Несовместное событие – событие, появление которого исключает появление других событий в одном и том же испытании. Совместное событие – событие, появление которого не исключает появление других событий в одном и том же испытании.

Случайные величины Случайная величина Дискретная случайная величина

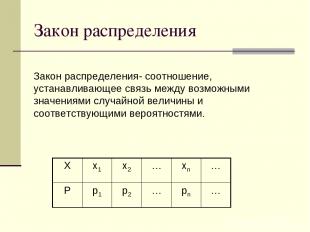
Закон распределения Закон распределения- соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями. X x1 x2 … xn … P p1 p2 … pn …

Пример Опыт состоит в подбрасывании игральной кости. Рассмотрим некоторые события, которые могут произойти в результате опыта: A – выпадает «шестерка»; B – выпадает нечетное число очков; C – выпадает число очков, кратное трем; D – выпадает число очков, некратное трем; E – выпадает меньше семи очков; F – выпадает больше шести очков. РЕШЕНИЕ. Ω={1,2,3,4,5,6} – совокупность всех исходов при подбрасывании игр. кости. Общее число исходов равно 6. Совокупности исходов для событий: A={6}, B={1,3,5}, C={3,6}, D={1,2,4,5}, E={1,2,3,4,5,6}, F={ }. Число исходов, благоприятствующих событию A, равно 1, событию B – 3, событию С – 2, событию D – 4, событию E – 6, событию F - 0.

Найдем отношение числа исходов, благоприятствующих событию, к общему числу исходов.

Химия & математика Задача. Известно, что реакция взаимодействия H3PO4 с KOH приводит к образованию трех различных солей (без учета условий). Какова вероятность появления в конце реакции: а)кислой соли; б)средней соли? Решение. Запишем формулы солей, которые можно получить: KH2PO4 - кислая соль; K2HPO4 – кислая соль; K3PO4 – средняя соль. Тогда: а)событие А = {получение кислой соли}, Р(А) = , где m=2, n=3; б)событие В = {получение средней соли}, Р(В) = , где m=1, n=3. Ответ: а) ;б) .

Применение в статистике

Физика & математика

Применение в астрономии

Применение в сельском хозяйстве Сэр Рональд Фишер (1890-1962)

Применение в медицине

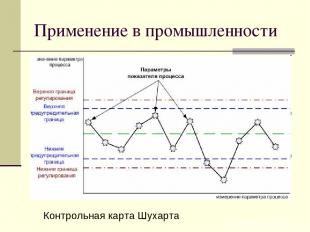
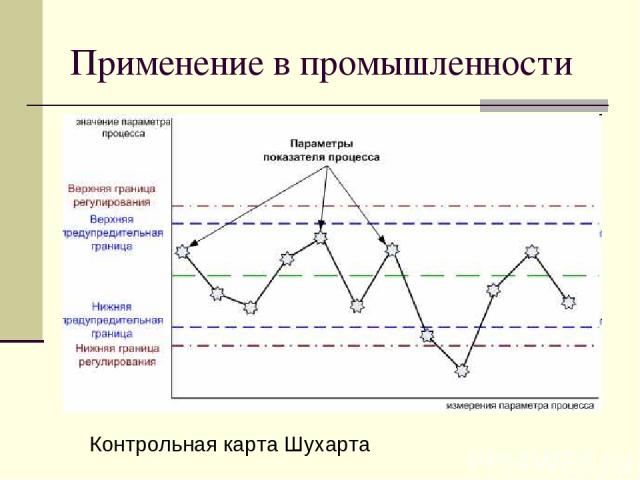
Применение в промышленности Контрольная карта Шухарта

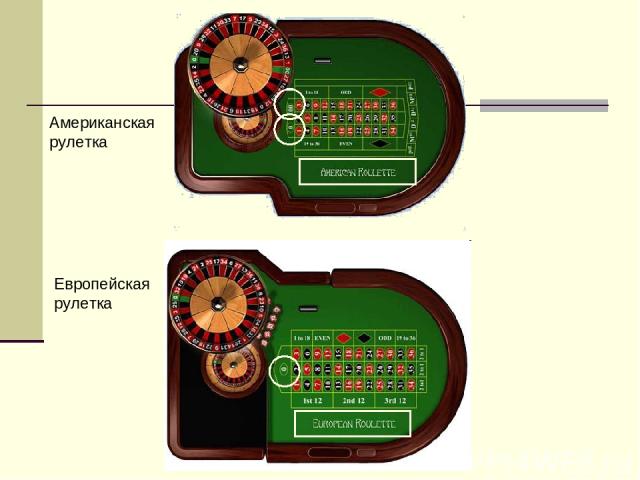
Рулетка Рулетка – самая старая из существующих игр в казино. Ее изобретение приписывали Блезу Паскалю, итальянскому математику Дону Паскуале и некоторым другим. В любом случае колесо рулетки впервые появилось в Париже в 1765 году.

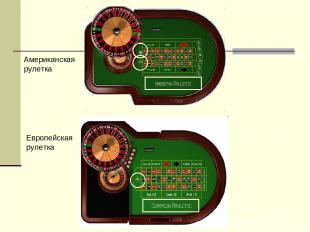
Американская рулетка Европейская рулетка

Применение в логических играх

Список использованной литературы и сайтов http://www.rulet.ca/ru/roulette/european.aspx http://ru.wikipedia.org/wiki/Теория_вероятностей http://www.teorver.ru/ Школьникам о вероятности в играх. Введение в теорию вероятностей для учащихся 8 – 11 классов. В. В. Афанасьев, М. А. Суворова. Учебник для учащихся 9 класса с углубленным изучением математики. Под редакцией Н. Я. Виленкина. Занимательные математические игры. Е. Я. Гик. Алгебра и начала анализа. 10 класс. А. Г. Мордкович, П. В. Семенов. Математические головоломки и развлечения. Мартин Гарднер. Вероятность и статистика. Е. А. Бунимович, В. А. Булычев. Математика в современном мире. Н. Г. Рычкова. Газета «Математика» №24 2010г.