Презентация на тему: «Комбинаторные задачи» 9 класс

Комбинаторные задачи и начальные сведения из теории вероятностей в курсе алгебры 9 класса. Парамонова Татьяна Павловна 5klass.net

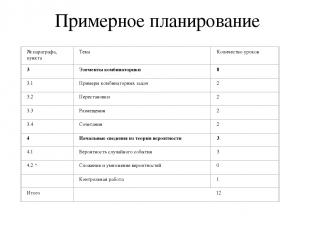
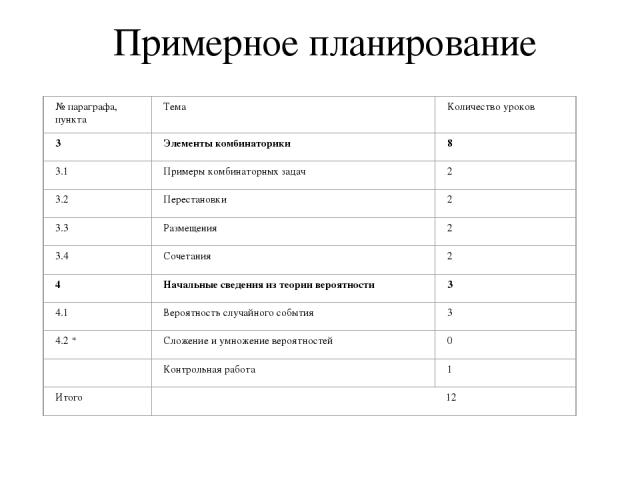
Примерное планирование

Комбинаторные задачи В науке и практике часто встречаются задачи, решая которые приходится составлять различные комбинации из конечного числа элементов и подсчитывать число этих комбинаций. Такие задачи получили название комбинаторных задач, а раздел математики, в котором рассматриваются подобные задачи, называют комбинаторикой. Методы комбинаторики находят широкое применение в физике, химии, биологии, экономике и других областях знаний.   Способы решения комбинаторных задач: v     перебор возможных вариантов; v     дерево возможных вариантов; v     комбинаторное правило умножения.

Способы решения комбинаторных задач: Перебор возможных вариантов Дерево возможных вариантов Комбинаторное правило умножения

Таких вариантов 10. Задача 9.2. У Ирины пять подруг: Вера, Зоя, Марина, Полина и Светлана, Она решила двух из них пригласить в кино. Укажите все возможные варианты выбора подруг. Сколько таких вариантов? Решение: Переберу возможные варианты:

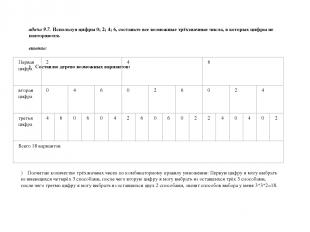
Задача 9.7. Используя цифры 0; 2; 4; 6, составьте все возможные трёхзначные числа, в которых цифры не повторяются. Решение:   1)      Составлю дерево возможных вариантов:   2)      Посчитаю количество трёхзначных чисел по комбинаторному правилу умножения: Первую цифру я могу выбрать из имеющихся четырёх 3 способами, после чего вторую цифру я могу выбрать из оставшихся трёх 3 способами, после чего третью цифру я могу выбрать из оставшихся двух 2 способами, значит способов выбора у меня 3*3*2=18.

Определение: Перестановкой из п элементов называется каждое расположение этих элементов в определённом порядке. Рп = п!   Задача 9.23. Ольга помнит, что телефон подруги оканчивается цифрами 5, 7, 8, но забыла, в каком порядке эти цифры следуют. Укажите наибольшее число вариантов, которые ей придётся перебрать, чтобы дозвониться подруге. Решение: Р3 = 3! = 1*2*3 = 6 (вариантов дозвона)   Задача 9.29. В расписании на понедельник шесть уроков: алгебра, геометрия биология, история, физкультура, химия. Сколькими способами можно составить расписание уроков на этот день так, чтобы два урока математики стояли рядом? Решение: Сначала буду рассматривать уроки алгебры и геометрии как один урок, тогда надо составить расписание не для 6 уроков, а для 5, т.е. Р5 = 5! = 120 (способами). При этом возможны 2! = 2 способа для расстановки уроков алгебры и геометрии относительно друг друга, значит по комбинаторному правилу умножения расписание на понедельник, соответствующее заданным требованиям, можно составить 120*2 = 240 (способами).  

Определение: Размещением из п элементов по к (к п) называется любое множество, состоящее из любых к элементов, взятых в определённом порядке из данных п элементов. Апк = п(п-1)(п-2)(п-3)….(п-(к-1)) Из определения следует, что два размещения из п элементов по к считаются различными, если они отличаются самими элементами или порядком их расположения. Задача 9.40. Сколькими способами может разместиться семья из трёх человек в четырёхместном купе, если других пассажиров в купе нет? Решение: Буду распределять (размещать) 4 места по 3 пассажирам, это возможно А43 = 4*3*2 = 24 способами. Задача 9.52. Сколько существует семизначных телефонных номеров, в которых все цифры различные и первая цифра отлична от нуля? Решение: Имея 10 цифр, я могу составить А107 = 10*9*8*7*6*5*4 семизначных телефонных номеров, в которых все цифры различны. Среди этих номеров имеются номера, начинающиеся с цифры 0, их число равно А96 = 9*8*7*6*5*4. Значит всего таких телефонных номеров будет А107 – А96 = 10*9*8*7*6*5*4 – 9*8*7*6*5*4 = 544320.    

Определение: Сочетанием из п элементов по к называется любое множество, составленное из к элементов, выбранных из данных п элементов. Спк = п!/к!(п-к)! В отличие от размещений в сочетаниях не имеет значения, в каком порядке указаны элементы. Два сочетания из п элементов по к отличаются друг от друга хотя бы одним элементом. Задача 9.57. В классе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать двоих из них для участия в математической олимпиаде? Решение: С72 = 7!/2!5! =7*6:2 = 21.   Задача 9. 68. Для ремонта школы прибыла бригада, состоящая из 12 человек. Трёх из них надо отправить на четвёртый этаж, а четырёх из оставшихся – на пятый. Сколькими способами это можно сделать? Решение: На четвёртый этаж можно отправить рабочих С123 = 12!/ 3!9! = 12*11*10/ 6 = 220 способами, после чего на пятый этаж можно отправить четверых из оставшихся 9 рабочих С94 = 9!/4!5! = 9*8*7*6/(1*2*3*4) =126 способами, т.е. по комбинаторному правилу умножения всего таких способов 220*126 =27720.

Начальные сведения из теории вероятности Событие, которое может произойти, может не произойти, называют случайным событием. Изучением закономерностей случайных событий занимается теория вероятностей.   Как часто наступает то или иное событие в большой серии испытаний со случайными исходами, которые происходят в одинаковых условиях?   Определение: Относительной частотой случайного события в серии испытаний называется отношение числа испытаний, в которых это событие наступило, к числу испытаний. Определение: Вероятностью события называется отношение числа благоприятных для него исходов к числу всех равновозможных исходов. Задача 9.75. В партии из 1000 деталей отдел технического контроля обнаружил 12 нестандартных деталей. Какова относительная частота появления нестандартных деталей? Решение: 12:100 = 0,012.   Задача 9.81. Для новогодней лотереи отпечатали 1500 билетов, из которых 120 выигрышных. Какова вероятность того, что купленный билет окажется выигрышным? Решение: 120:1500 = 0,08 = 8%.

Задача 9.93. На полке стоят 12 книг, из которых 4 – это учебники. С полки снимают наугад 6 книг. Какова вероятность того, что 3 из них окажутся учебниками? Решение: Пусть А – событие, состоящее в том, 3 из 6 снятых с полки книг, окажутся учебниками, тогда количество равновозможных исходов «снять 6 книг из 12» равно С126 при этом количество благоприятных исходов «снять 3 учебника из 4» равно С43, после чего количество благоприятных исходов «снять 3 неучебника из 8 неучебников» равно С83 и по правилу комбинаторного умножения всего благоприятных исходов события А будет С43С83. Значит Р(А) = С43С83/С126 = (4!/3!1!)(8!/3!5!)/(12!/6!6!) = 4!8!6!6!/(3!3!5!12!) = 8:33 =24%.