Презентация на тему: Синус и косинус угла

Синус и косинус угла «Алгебраическое» определение Харьковский В.З.

1-й блок слайдов Харьковский В.З.

Что такое косинус угла ? Это число, которое можно определить следующим образом: Харьковский В.З.

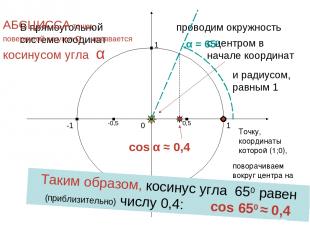
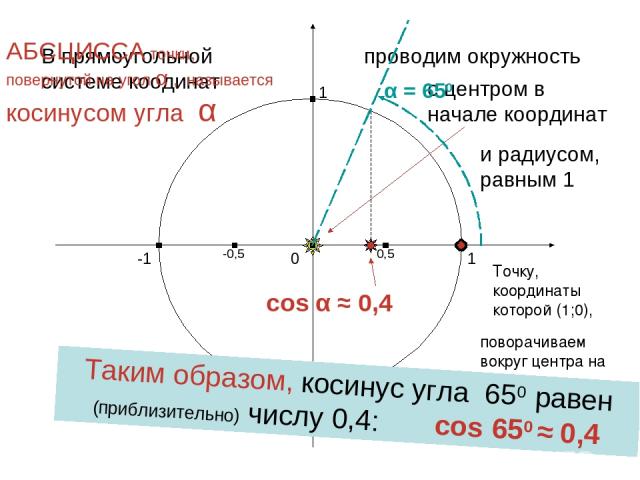
cos α ≈ 0,4 1 0 -1 1 -1 В прямоугольной системе коодинат проводим окружность с центром в начале координат и радиусом, равным 1 Точку, координаты которой (1;0), поворачиваем вокруг центра на угол α АБСЦИССА точки, повернутой на угол α , называется косинусом угла α α = 650 0,5 -0,5 Таким образом, косинус угла 650 равен (приблизительно) числу 0,4: cos 650 ≈ 0,4 Харьковский В.З.

ЗАПОМНИМ: поворот точки на положительный угол выполняется против часовой стрелки поворот точки на отрицательный угол выполняется по часовой стрелке Харьковский В.З.

Найдем теперь косинус другого угла, например – угла 217 0 Харьковский В.З.

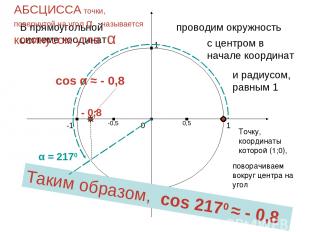
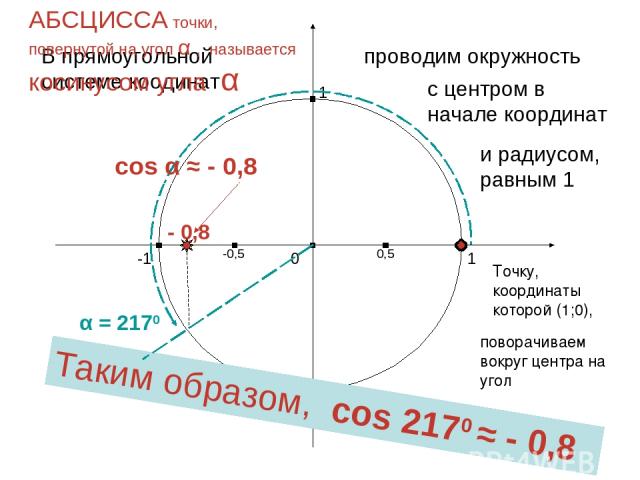
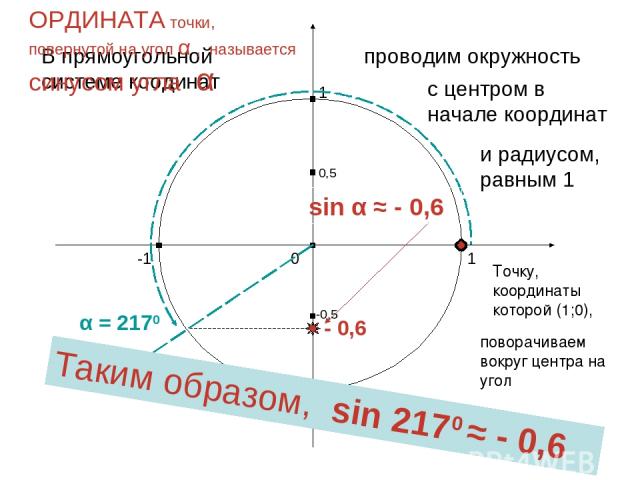
1 0 -1 1 -1 В прямоугольной системе коодинат проводим окружность с центром в начале координат и радиусом, равным 1 Точку, координаты которой (1;0), поворачиваем вокруг центра на угол α АБСЦИССА точки, повернутой на угол α , называется косинусом угла α α = 2170 0,5 -0,5 Таким образом, cos 2170 ≈ - 0,8 - 0,8 cos α ≈ - 0,8

Попробуйте теперь сами: выполните чертеж и определите (приближенно) косинус угла -3100 Харьковский В.З.

Помните: поворот точки на отрицательный угол выполняется по часовой стрелке Харьковский В.З.

Итак, вам следует: в прямоугольной системе координат построить окружность (центр – начало координат, радиус – единичный отрезок); отметить точку (1;0); повернуть ее (вокруг начала координат) на угол -3100; определить абсциссу получившейся точки – это и есть косинус угла -3100; записать результат: cos (-3100) ≈ … только после выполнения этого задания можете продолжить просмотр Харьковский В.З.

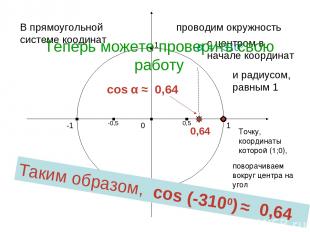
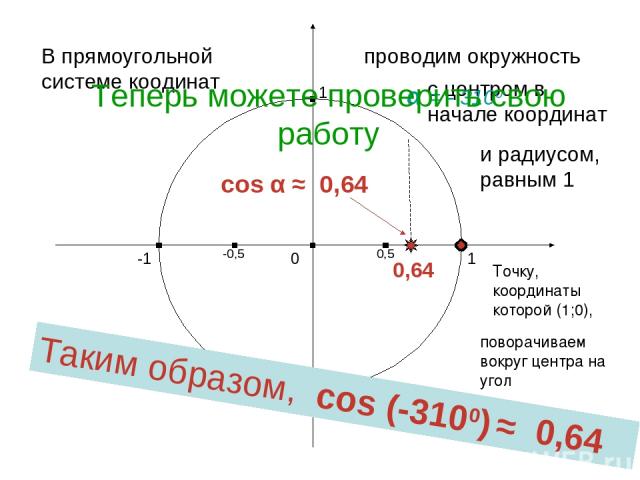
cos α ≈ 0,64 1 0 -1 1 -1 В прямоугольной системе коодинат проводим окружность с центром в начале координат и радиусом, равным 1 Точку, координаты которой (1;0), поворачиваем вокруг центра на угол α α = - 3100 0,5 -0,5 Таким образом, cos (-3100) ≈ 0,64 0,64 Теперь можете проверить свою работу Харьковский В.З.

2-й блок слайдов Харьковский В.З.

Что такое синус угла ? Это число, которое можно определить следующим образом: Харьковский В.З.

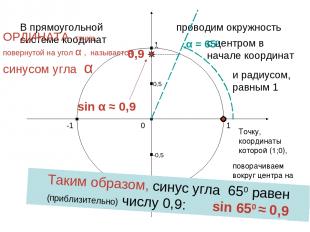
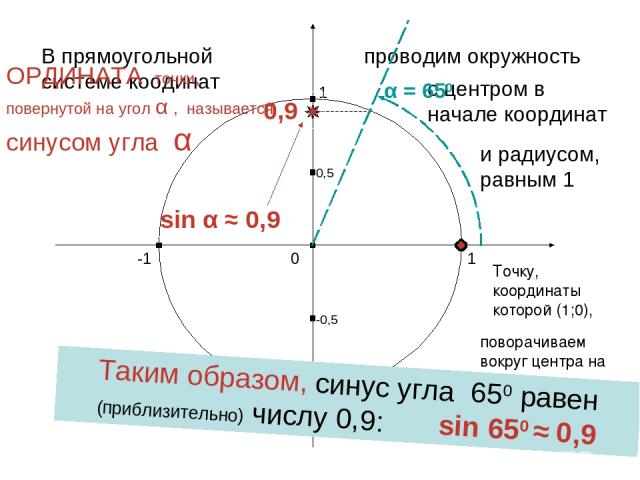
1 0 -1 1 -1 В прямоугольной системе коодинат проводим окружность с центром в начале координат и радиусом, равным 1 Точку, координаты которой (1;0), поворачиваем вокруг центра на угол α ОРДИНАТА точки, повернутой на угол α , называется синусом угла α α = 650 0,5 -0,5 Таким образом, синус угла 650 равен (приблизительно) числу 0,9: sin 650 ≈ 0,9 sin α ≈ 0,9 0,9 Харьковский В.З.

Найдем теперь синус другого угла, например – угла 217 0 Харьковский В.З.

1 0 -1 1 -1 В прямоугольной системе коодинат проводим окружность с центром в начале координат и радиусом, равным 1 Точку, координаты которой (1;0), поворачиваем вокруг центра на угол α ОРДИНАТА точки, повернутой на угол α , называется синусом угла α α = 2170 0,5 -0,5 - 0,6 sin α ≈ - 0,6 Таким образом, sin 2170 ≈ - 0,6

Снова попробуйте сами: с помощью имеющегося у Вас чертежа определите (приближенно) синус угла -3100

Помните: синус угла – это ордината точки Харьковский В.З.

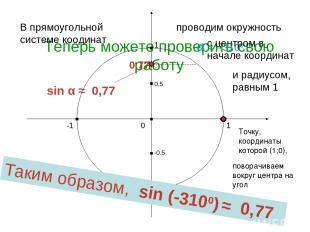
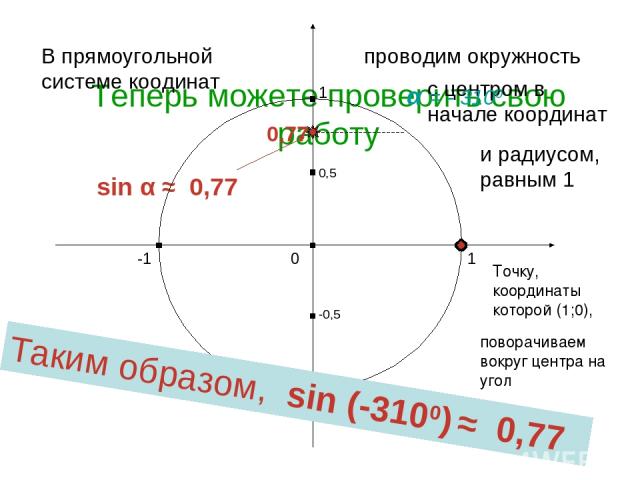
Теперь можете проверить свою работу sin α ≈ 0,77 1 0 -1 1 -1 В прямоугольной системе коодинат проводим окружность с центром в начале координат и радиусом, равным 1 Точку, координаты которой (1;0), поворачиваем вокруг центра на угол α α = - 3100 0,5 -0,5 0,77 Таким образом, sin (-3100) ≈ 0,77 Харьковский В.З.

3-й блок слайдов Харьковский В.З.

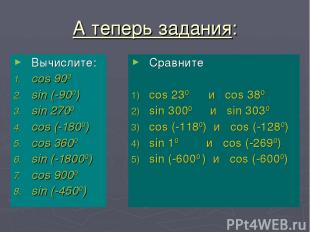
А теперь задания: Вычислите: cos 900 sin (-900) sin 2700 cos (-1800) cos 3600 sin (-18000) cos 9000 sin (-4500) Сравните cos 230 и cos 380 sin 3000 и sin 3030 cos (-1180) и cos (-1280) sin 10 и cos (-2690) sin (-6000 ) и cos (-6000) Харьковский В.З.

1 0 -1 1 -1 Харьковский В.З.

А это – для «продвинутых»: Сравните: sin 1230 и sin 560 Вычислите: sin 1600 · cos (-2000) · cos 8100 · sin 10000 Харьковский В.З.

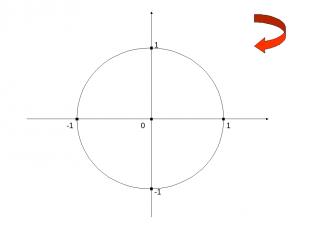
1 0 -1 1 -1 Харьковский В.З.

Демонстрация слайдов окончена Харьковский В.З.