Презентация на тему: Синус , косинус, тангенс и котангенс угла из промежутка [0°; 180°]

Синус , косинус, тангенс и котангенс угла из промежутка [0°; 180°]

Продолжите фразу: Эти соотношения позволяют в прямоуголь-ном треугольнике Аналогичную задачу часто приходитсярешать и в произвольном треугольнике:остороугольном и тупоугольном.

Необходимо понять!!! 1. Если существуют соотношения между сторонами и углами в произвольном треугольнике, то что следует считать синусом, косинусом, тангенсом острого или тупого угла произвольного треугольника?2. Если существуют соотношения между сторонами и углами в произвольном треугольнике, то каковы эти соотношения?

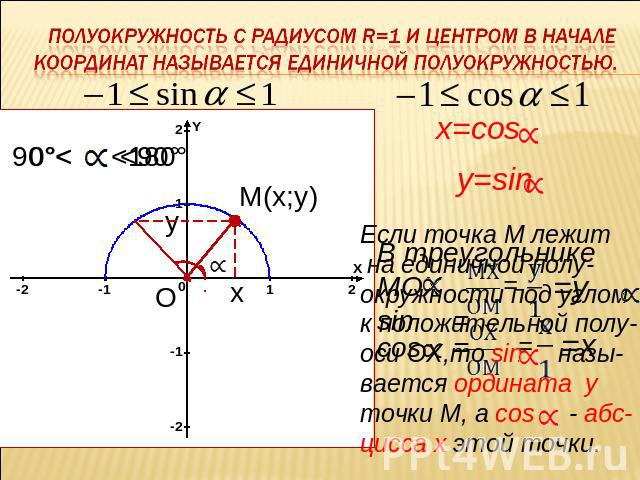
ПОЛУОКРУЖНОСТЬ С РАДИУСОМ R=1 И ЦЕНТРОМ В НАЧАЛЕ КООРДИНАТ НАЗЫВАЕТСЯ ЕДИНИЧНОЙ ПОЛУОКРУЖНОСТЬЮ. Если точка М лежит на единичной полу-окружности под углом к положительной полу-оси ОХ,то sin назы-вается ордината у точки М, а сos - абс-цисса х этой точки.

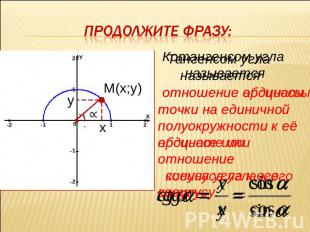
Продолжите фразу: отношение абсциссыточки на единичной полуокружности к её ординате или отношение косинуса угла к его синусу.

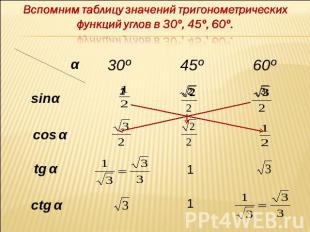
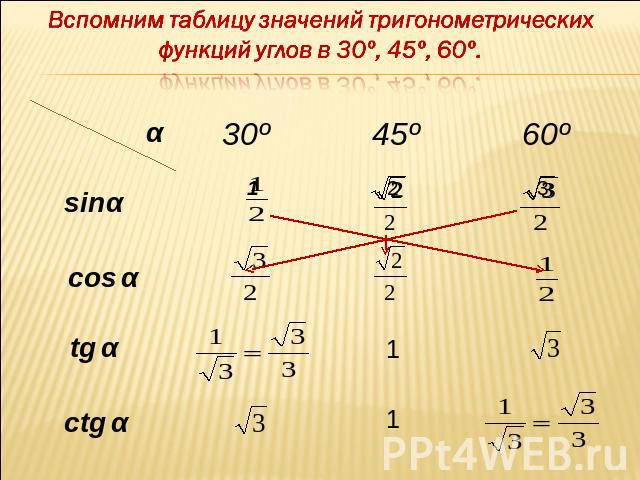
Вспомним таблицу значений тригонометрических функций углов в 30º, 45º, 60º.

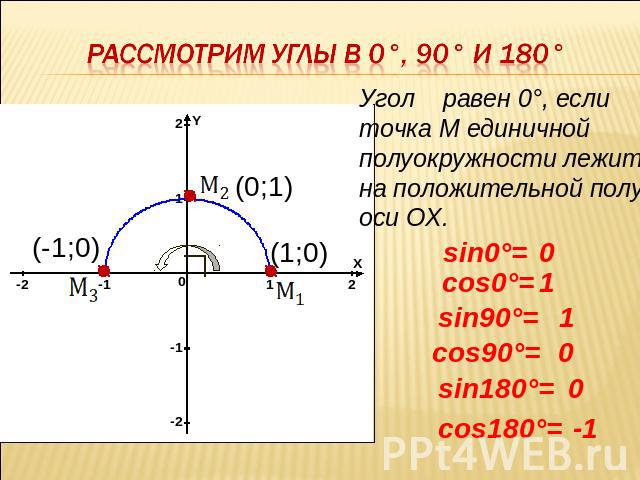
Рассмотрим Углы в 0°, 90° и 180° Угол равен 0°, еслиточка М единичнойполуокружности лежит на положительной полу-оси ОХ.

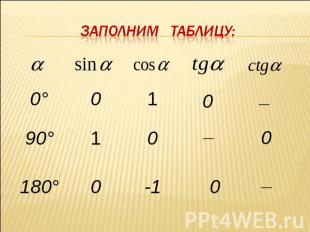
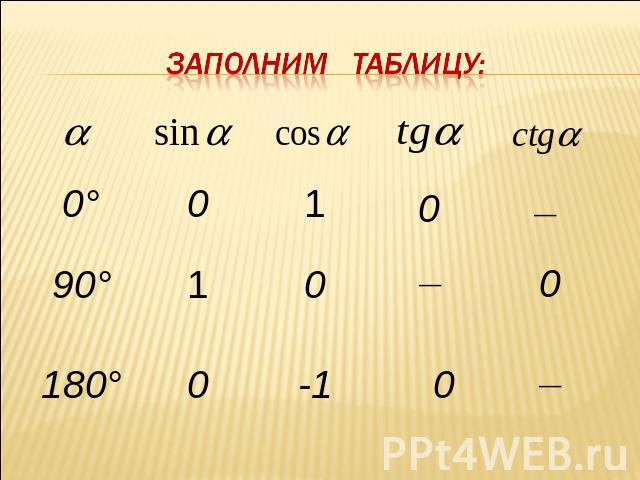
Заполним таблицу:

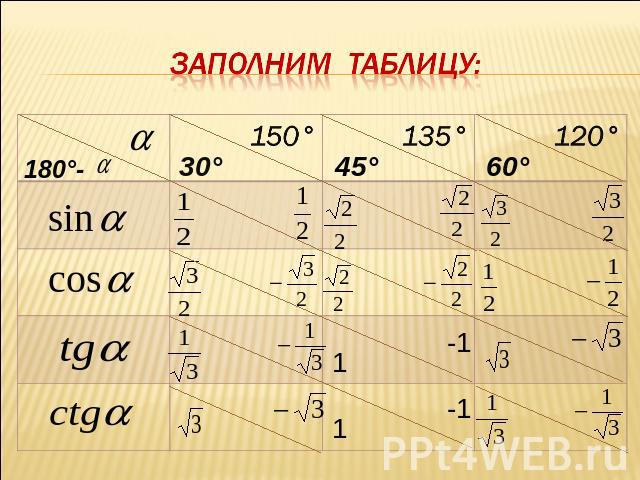
Формулы приведения. Если сумма двух углов равна 90°,то синус одного угла равен косину-су другого и наобо-рот.

Продолжите фразу: Если сумма двух углов равна 90°, тотангенс одного из них равен котангенсу другого.

Формулы приведения. Если сумма двух углов равна 180°,то их синусы равны,а косинусы противо-положны.

Продолжите фразу: Если сумма двух углов равна 180°, то их тангенсы и котангенсы

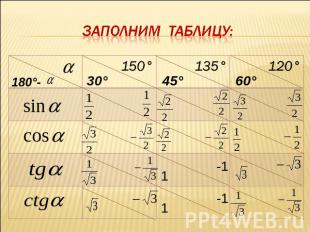
Заполним таблицу:

Основные тождества. М(х;у) лежит на окружности с центром(0;0) и радиусом r=1.Основное тригономет-рическое тождество.