Презентация на тему: Комбинаторные задачи. Комбинаторика

Комбинаторные задачи.Комбинаторика. Г. Екатеринбург Моу-гимназия № 13 Учитель Анкина т.с. расположение перестановки выбор

При создании этой презентации были использованы следующие материалы: А. Г. Мордкович, П. В. Семёнов. Алгебра 9. Учебник. Часть 1. Изд. Мнемозина. Москва 2010. Материалы презентации «Российская академия образования. Институт педагогических исследований одарённости детей (ИПИО).Программно-методический комплекс "Элементы теории множеств и комбинаторики " для среднего и дополнительного образования. Ю.В. Михеев, А.А. Никитин, Г.А. Сапрыкина, Л.С. Шум»: слайды №23. (http://www.openclass.ru/dig-resource/150925). Картинки и изображения с сайта http://images.yandex.ru/.

Комбинаторика. Комбинаторика – это раздел математики, в котором изучаются вопросы выбора или расположения элементов множества в соответствии с заданными правилами. Комбинаторика рассматривает конечные множества.

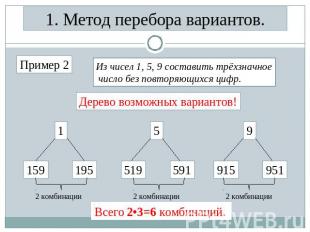
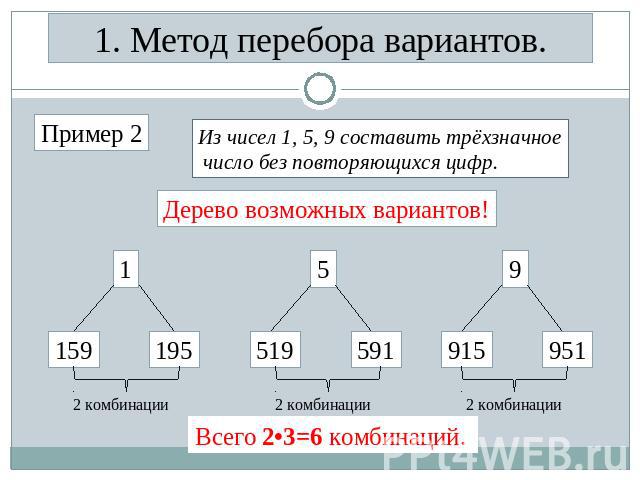
1. Метод перебора вариантов. Из чисел 1, 5, 9 составить трёхзначное число без повторяющихся цифр. Дерево возможных вариантов! Пример 2 Всего 2•3=6 комбинаций.

Методы перебора (дерево возможных вариантов). Из цифр 2, 4, 7 составить трёхзначное число, в котором ни одна цифра не может повторяться более двух раз. а)Сколько таких чисел начинается с 2? б) Сколько всего таких чисел можно составить? 1способ: построим дерево возможных вариантов, если первая цифра числа 2 2 способ: 1)Числа без повторений: 2)Числа, в которых повторяется 2: 3)Числ0, в котором повторяется 4: 4)Числ0, в котором повторяется 7: а)Ответ: 8 чисел. б)Ответ: 24 числа.

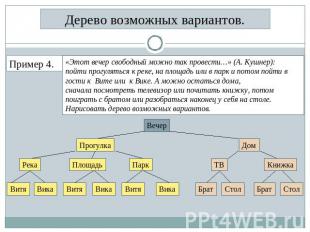
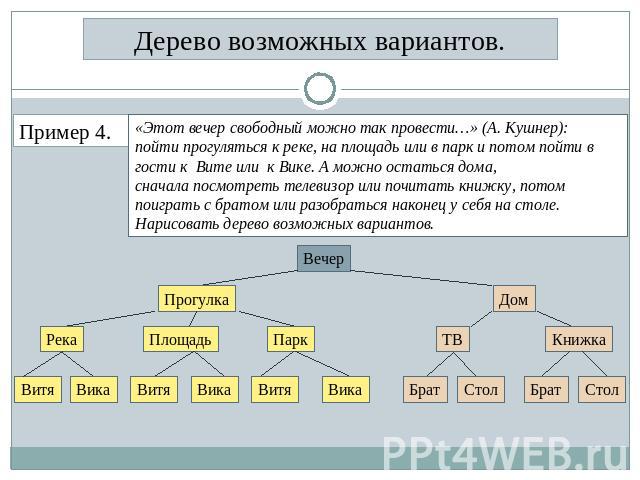
Дерево возможных вариантов. Пример 4. «Этот вечер свободный можно так провести…» (А. Кушнер): пойти прогуляться к реке, на площадь или в парк и потом пойти в гости к Вите или к Вике. А можно остаться дома, сначала посмотреть телевизор или почитать книжку, потом поиграть с братом или разобраться наконец у себя на столе. Нарисовать дерево возможных вариантов.

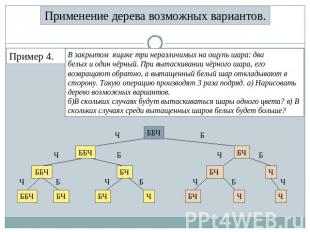
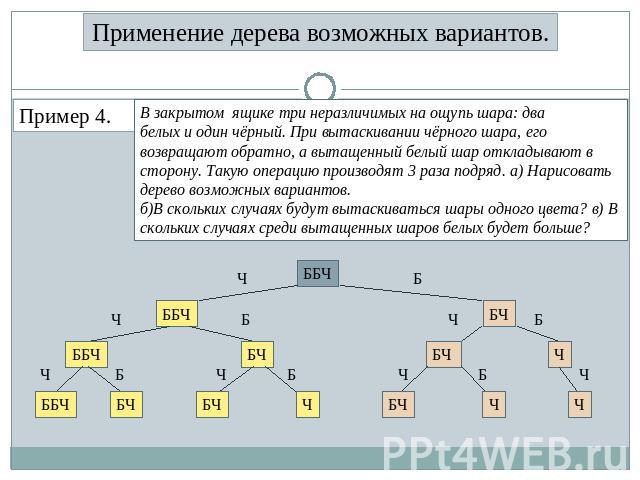
Применение дерева возможных вариантов. Пример 4. В закрытом ящике три неразличимых на ощупь шара: два белых и один чёрный. При вытаскивании чёрного шара, его возвращают обратно, а вытащенный белый шар откладывают в сторону. Такую операцию производят 3 раза подряд. а) Нарисовать дерево возможных вариантов. б)В скольких случаях будут вытаскиваться шары одного цвета? в) В скольких случаях среди вытащенных шаров белых будет больше?

2.Правило умножения. На завтрак можно выбрать булочку, кекс, пряники или печенье, запить можно чаем, соком или кефиром. Сколько вариантов завтрака есть? Для того, чтобы найти число всех возможных исходов (вариантов) независимого проведения двух испытаний А и В, надо перемножить число всех исходов испытания А на число всех исходов испытания В Испытание А имеет 3 варианта (исхода), а испытание В-4, всего вариантов независимых испытаний А и В 3•4=12.

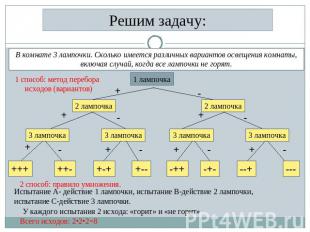
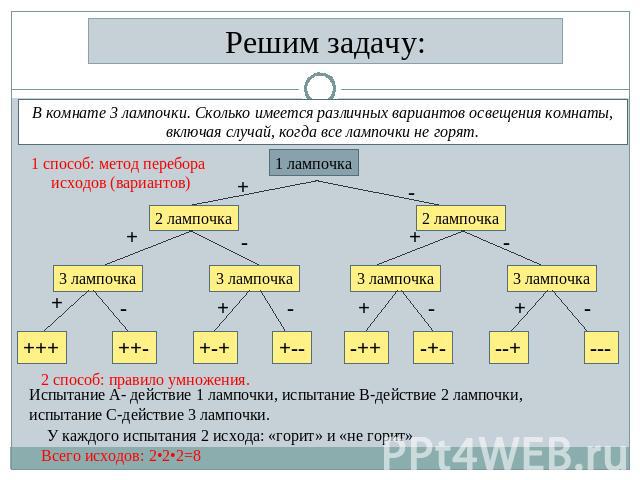
Решим задачу: В комнате 3 лампочки. Сколько имеется различных вариантов освещения комнаты, включая случай, когда все лампочки не горят. 1 способ: метод перебора исходов (вариантов) 2 способ: правило умножения. Испытание А- действие 1 лампочки, испытание В-действие 2 лампочки, испытание С-действие 3 лампочки. У каждого испытания 2 исхода: «горит» и «не горит» Всего исходов: 2•2•2=8

Семейный ужин. Пример 1. В семье 6 человек, а за столом в кухне 6 стульев. Было решено каждый вечер перед ужином рассаживаться на эти 6 стульев по-новому. Сколько дней члены семьи смогут делать это без повторений?

3. « Эн факториал»-n!. 1•2•3•4•5•6=720 Определение. Произведение подряд идущих первых n натуральных чисел обозначают n! и называют «эн факториал»: n!=1•2•3•…•(n-1)•n. Удобная формула!!! n!=(n-1)!•n

Их разыскивает полиция… Пример 2. Сколькими способами 4 вора могут по одному разбежаться на все 4 стороны. 1•2•3•4=4!=24

Расписание уроков. Пример 3. В 9 классе в среду 7 уроков: алгебра, геометрия, литература, русский язык, английский язык, биология и физкультура. Сколько вариантов расписания можно составить? Расставляем предметы по порядку Всего вариантов расписания

Перестановки и их число. Определение. Перестановкой называется множество из n элементов, записанных в определённом порядке. Теорема о перестановках элементов конечного множества. n различных элементов можно расставить по одному на n различных мест ровно n! способами.