Презентация на тему: «Вероятность» 9 класс

Теория вероятностей и статистика 9 класс Глава 12. Числовые характеристики случайных величин 5klass.net

Результаты обучения. В результате изучения материала главы 12 учащийся должен: знать определение математического ожидания конечной случайной величины, понимать, что математическое ожидание является обобщением среднего арифметического значений величины; знать свойства математического ожидания и уметь использовать их при решении простых задач; знать, что важным свойством распределения случайной величины является рассеивание величины, уметь вычислять дисперсию и стандартное отклонение; знать формулы математического ожидания и дисперсии числа успехов в серии испытаний Бернулли.

П.53. Математическое ожидание случайной величины. Для введения понятия «математическое ожидание случайной величины» необходимо разобрать задачу п.53. Для проведения лотереи изготовили 100 билетов. Из них 1 билет с выигрышем в 500 р., 10 билетов с выигрышем по 100 р. и остальные 89 билетов без выигрыша. Какой средний выигрыш соответствует 1 билету? Выигрыш является случайной величиной Х, которая может принимать значение 0;100; 500, с вероятностью 0,89; 0,1 и 0,01. Если покупатель приобретает все 100 билетов, то выигрыш составит 1500 руб, следовательно выигрыш, соответствующий одному билету в 100 раз меньше. 15 руб. (0·89+10·100+1·500):100 = 0·0,89+100·0,1+500·0,01=15. 15 руб – это среднее значение случайной величины. Оно называется математическим ожиданием случайной величины. Значения 0 100 500 Вероятность 0,89 0,1 0,01

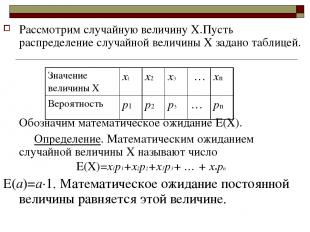
Рассмотрим случайную величину Х.Пусть распределение случайной величины Х задано таблицей. Обозначим математическое ожидание Е(Х). Определение. Математическим ожиданием случайной величины Х называют число Е(Х)=х1р1+х2р2+х3р3+ … + хnрn Е(а)=а·1. Математическое ожидание постоянной величины равняется этой величине. Значение величины Х х1 х2 х3 … хn Вероятность р1 р2 р3 … рn

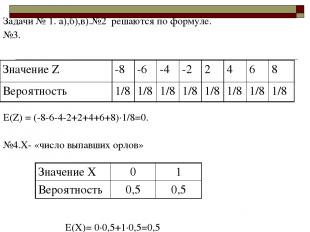
Задачи № 1. а),б),в).№2 решаются по формуле. №3. Е(Z) = (-8-6-4-2+2+4+6+8)·1/8=0. №4.Х- «число выпавших орлов» Е(Х)= 0·0,5+1·0,5=0,5 Значение Z -8 -6 -4 -2 2 4 6 8 Вероятность 1/8 1/8 1/8 1/8 1/8 1/8 1/8 1/8 Значение Х 0 1 Вероятность 0,5 0,5

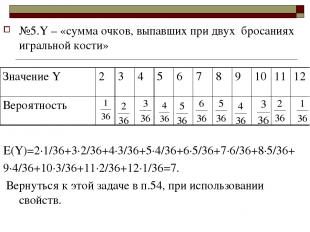
№5.Y – «сумма очков, выпавших при двух бросаниях игральной кости» Е(Y)=2·1/36+3·2/36+4·3/36+5·4/36+6·5/36+7·6/36+8·5/36+ 9·4/36+10·3/36+11·2/36+12·1/36=7. Вернуться к этой задаче в п.54, при использовании свойств. Значение Y 2 3 4 5 6 7 8 9 10 11 12 Вероятность

Задача № 9. Х – «число клеток в подбитом корабле» Е(Х)=0·0,8 +1·0,04 +2·0,06 +3·0,06+4·0,04 = 0,5. Е(Х) = 0,5. Значение Х 0 1 2 3 4 Вероятность 0,8 0,04 0,06 0,06 0,04

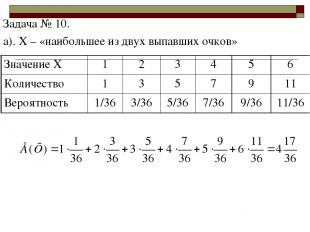
Задача № 10. а). Х – «наибольшее из двух выпавших очков» Значение Х 1 2 3 4 5 6 Количество 1 3 5 7 9 11 Вероятность 1/36 3/36 5/36 7/36 9/36 11/36

№10 (б). Х – «наименьшее из двух выпавших очков» Значение 1 2 3 4 5 6 Количество 11 9 7 5 3 1 Вероятность 11/36 9/36 7/36 5/36 3/36 1/36

П. 54. Свойства математического ожидания Свойство1.Пусть Х – случайная величина, а – некоторое число. Рассмотрим случайную величину Y=аХ. Тогда Е(Y)=аЕ(Х). Свойство 2. Пусть U и V – две случайные величины. Тогда U + V – также случайная величина, и при этом Е(U+V) = E(U)+E(V). Это значит, что математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий.

Задача № 1. Х – «число очков, выпавших на одной игральной кости» Е(Х) = 3,5 Тогда при пяти бросаниях математическое ожидание равно а).3,5·5 = 17,5 б).3,5·7 = 24,5 в).3,5·100 = 350 г).3,5·k = 3,5k Задача № 2. Применение свойств.

Задача № 3. р=1/11. Е(Х) = 1/11·(-3-2-1+0+1+2+3+4+5+6+7)=2 р = 1/9. Е(Y)= 1/9·(1+2+3+4+5+6+7+8+9) = 5 a). Z=X+Y, E(Z) = E(X)+E(Y) E(Z)= 2+5 = 7 б). Z=X-Y E(Z) = 2-5 = -3. Значение Х -3 -2 -1 0 1 2 3 4 5 6 7 Вероятность р р р р р р р р р р р Значение Y 1 2 3 4 5 6 7 8 9 Вероятность р р р р р р р р р

Задача № 5. Т.к. бросаний 5, то всего событий 32. Х – «выпадение орлов» Е(Х)=1/32·(0+ 1·5+2·10+3·10+4·5+5·1)= 80 · 1/32 = 2,5 Е(Х) = 2,5 Задача № 6 разбирается подробно в п.58. Значение Х 0 1 2 3 4 5 Вероятность 1/32 5/32 10/32 10/32 5/32 1/32

П.56- 57. Дисперсия и стандартное отклонение. Свойства дисперсии. Дисперсия - мера рассеивания.(п.55) Дисперсией случайной величины Х называют математическое ожидание случайной величины (Х –Е(Х))². D(X) = E((Х –Е(Х))²) Стандартное отклонение σ = √D(X) Свойства дисперсии. 1.Пусть Х – случайная величина. Рассмотрим случайную величину Y = аХ, где а - некоторое число. Тогда D(Y) =a²D(X) 2. Пусть Х – случайная величина . Рассмотрим случайную величину Y = X + a. Тогда D(Y) = D(X)

Задача № 2. Проводится одно испытание Бернулли, с вероятностью успеха р. Случайная величина S – «число успехов». Найти D(S). Е(S) = р D(X) = E((Х –Е(Х))²) D(S) = р²(1- р)+(1- р)²р = р(1- р)(р + 1- р) = р(1- р) = р - р² Значение S 0 1 Вероятность 1-р р Значение S – E(S) - р 1-р Вероятность 1-р р

Задача № 3. D(X) = E((Х –Е(Х))²) а).Е(Х) = -2·0,3+0·0,5+3·0,2=0 D(X)=4·0,3+0·0,5+9·0,2=1,2+1,8=3 б). Аналогично. (Х –Е(Х))² 4 0 9 Вероятность 0,3 0,5 0,2

Задача №4.б). Вычислить дисперсию случайной величины Х. D(X) = E((Х –Е(Х))²) Е(Х) = 3 Е((Х-Е(Х))²) = 25·0,1+9·0,1+4·0,2+4·0,6= 6,6 D(X) = 6,6 Задачи № 5,6 решаются аналогично. Значения Х -2 0 1 5 Вероятность 0,1 0,1 0,2 0,6 Значения Х – Е(Х) -5 -3 -2 2 Вероятность 0,1 0,1 0,2 0,6

Задача № 7. а). Случайная величина Х принимает значения от 0 до 6 с равными вероятностями, т.е. р =1/7. Найти D(X). D(X) = E((Х –Е(Х))²) Е(Х)=21·1/7 =3 Значения Х- Е(Х) от -3 до 3. Тогда D(Х)=4. б). Случайная величина Y принимает значения от 1 до 7, т.е. Y = Х + 1. Следовательно, по свойству дисперсии D(Y) = D(X). Т.е. D(Y) = 4.

Задача № 8. При решении используются свойства дисперсии. a). D(X) = 3, Y=3X, D(Y)= 9D(X), D(Y)=27 б). Y=X+5. D(Y)=D(X) D(Y)=3. е). Y=-5X-7. D(Y)= 25D(X)=75. Остальные решаются аналогично.

П. 58. Математическое ожидание числа успехов в серии испытаний Бернулли Если S – число успехов в серии n независимых испытаний Бернулли с вероятностью успеха р, то Е(S) = np.

Задача № 1. 2000 – окуней и 1000 – карасей. Всего 3000 рыб. Найти ожидаемое число карасей. E(S) = np S = 0;1; 2;4; …;30 Е(S) = 30p E(S) = 10

Задача № 3. n=120 а).S – «число очков кратно 3» При бросании игральной кости с равной вероятностью 1/6 выпадают 1, 2, 3,4,5,6. Успехов 2 (значения 3 и 6). Следовательно вероятность события Х при однократном бросании равна 1/3. Т.е. Е(S) = 120∙1/3 = 40. б). Аналогично.

Задача № 4. Вероятность успеха 0,25. Следовательно Е(S)=16·0.25=4. Т.е. ожидаемое число правильных ответов 4. Задача №5. Математическое ожидание случайной величины «число выпадений острием вверх» равно 135. n=300. Найти р. Е(S) = np. р·300 = 135, p = 0,45

П. 59. Дисперсия числа успехов. Дисперсия числа успехов S в серии испытаний Бернулли вычисляется по формуле D(S) = npq. n – число испытаний Бернулли р – вероятность успеха q – вероятность неудачи

Задача № 1. n = 100 p = 0,36, следовательно q = 0,64. D(S) = 0,36·0,64·100 = 23,04 σ = √D(S) σ = √23,04 = 4,8 Задача № 2. а). Х – «выпавшее число очков кратно 3» D(X) = 3000

Задача № 3. S – число попаданий серии выстрелов по мишени. р – вероятность попадания (вероятность успеха) Найти дисперсию величины S. а). D(X) = npq. р=0,3, тогда вероятность неудачи равна 0,7. число выстрелов равно 100. Тогда дисперсия равна 21. в). При 2500 выстрелах дисперсия равна 525.

К задаче № 4 даны рекомендации в ответе.