Презентация на тему: Случайные события и вероятность

Случайные события и вероятность Справочное пособие для учащихся Подготовила: Теленгатор С.В. учитель математики МОУ «Лицей №15» им. акад. Ю.Б. Харитона

Определение вероятности В толковом словаре С.И. Ожегова и Н.Ю. Шведовой: «Вероятность – возможность исполнения, осуществимости чего-нибудь». Основатель современной теории вероятностей А.Н.Колмогоров: «Вероятность математическая – это числовая характеристика степени возможности появления какого-либо определенного события в тех или иных определенных, могущих повторяться неограниченное число раз условиях».

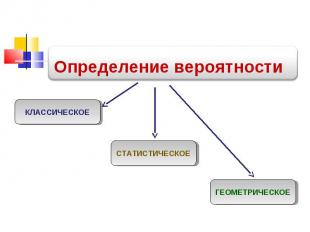
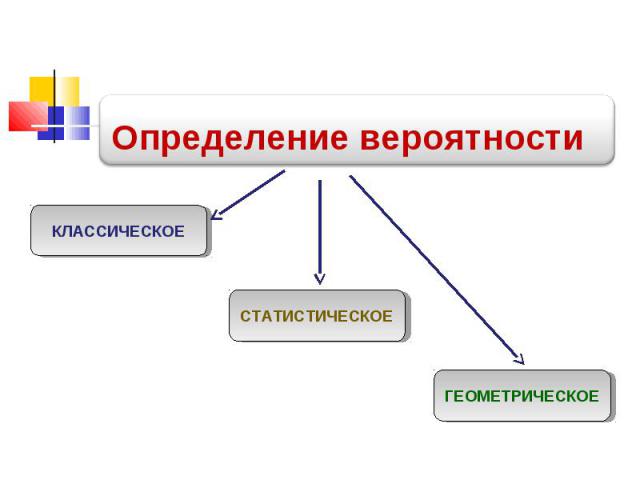
Определение вероятности

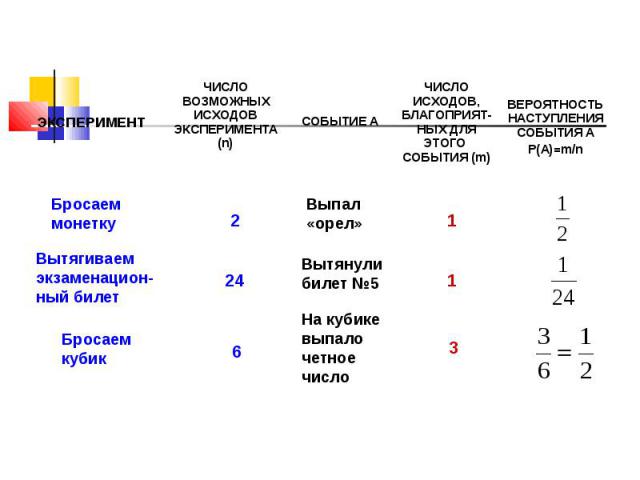
Классическое определение вероятности Вероятностью Р наступления случайного события А называется отношение , где n – число всех возможных исходов эксперимента, а m – число всех благоприятных исходов:

Пьер-Симо н Лапла с (23.3.1749, Бомон-ан-Ож, Нормандия, — 5.3.1827, Париж) Классическое определение вероятности было впервые дано в работах французского математика Лапласа.

Задача ГИА На 100 электрических лампочек в среднем приходится 25 бракованных. Какова вероятность купить исправную лампочку? Опыт имеет 100 равновозможных исходов, т.е. п = 100. Число благоприятных исходов т = 100 – 25 = 75. Вероятность того, что лампочка будет исправной

Жан Лерон Даламбер (1717 -1783) Великий французский философ и математик вошел в историю теории вероятностей со своей знаменитой ошибкой, суть которой в том, что он неверно определил равновозможность исходов в опыте всего с двумя монетами! В одной из статей, написанных для знаменитой Французской энциклопедии, Даламбер приводит такое рассуждение: "Бросают две одинаковые монеты. Какова вероятность того, что выпадут два орла? У этого опыта три равновозможных исхода: выпадут два орла, выпадет орел и решка, выпадут две решки. Значит, искомая вероятность будет 1/3"

Подбрасываем две одинаковые монеты. Какова вероятность того, что они упадут на одну и ту же сторону? Решение Даламбера: Опыт имеет три равновозможных исхода: 1) обе монеты упадут на «орла»; 2) обе монеты упадут на «решку»; 3) одна из монет упадет на «орла», другая на «решку». Из них благоприятными будут два исхода. Правильное решение: Опыт имеет четыре равновозможных исхода: 1) обе монеты упадут на «орла»; 2) обе монеты упадут на «решку»; 3) первая монета упадет на «орла», вторая на «решку»; 4) первая монета упадет на «решку», вторая на «орла». Из них благоприятными будут два исхода.

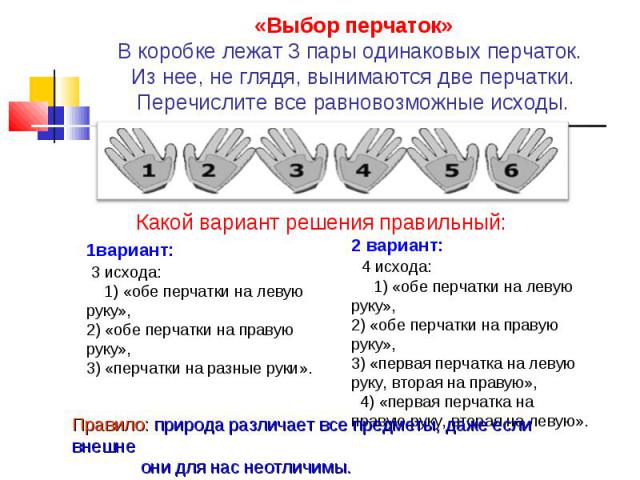
«Выбор перчаток» В коробке лежат 3 пары одинаковых перчаток. Из нее, не глядя, вынимаются две перчатки. Перечислите все равновозможные исходы. Какой вариант решения правильный: 1вариант: 3 исхода: 1) «обе перчатки на левую руку», 2) «обе перчатки на правую руку», 3) «перчатки на разные руки». 2 вариант: 4 исхода: 1) «обе перчатки на левую руку», 2) «обе перчатки на правую руку», 3) «первая перчатка на левую руку, вторая на правую», 4) «первая перчатка на правую руку, вторая на левую». Правило: природа различает все предметы, даже если внешне они для нас неотличимы.

Задача №1. Чтобы определить, как часто встречаются в лесопарке деревья разных пород, ребята провели следующие эксперименты. Каждый выбрал свою тропинку и по пути следования записывал породу каждого десятого дерева. Результаты были занесены в таблицу: Оцените вероятность того, что выбранное наугад в этом парке дерево будет: а) сосной; б) хвойным; в) лиственным. Указание. Ответ запишите в виде десятичной дроби с тремя знаками после запятой.

Решение: а) A={выбранное наугад в парке дере о - сосна} б) В ={выбранное наугад в парке дерево - хвойное} в) C={выбранное наугад в парке дерево - лиственное}

Самостоятельная работа