Презентация на тему: Комбинаторика и теория вероятности

Введение в комбинаторику и теорию вероятностей. Комбинаторика Факториал Перестановки Размещения Сочетания Частота и вероятность Сложение вероятностей Умножение вероятностей 900igr.net

Комбинаторика. «комбинаторика» происходит от латинского слова combinare – «соединять, сочетать». Определение. Комбинаторика – это раздел математики, посвящённый задачам выбора и расположения предметов из различных множеств.

Пример 2. Сколько трёхзначных чисел можно составить из цифр 1, 3, 5, 7, используя в записи числа каждую цифру не более одного раза? 1 3 5 7 3 3 3 5 5 5 7 7 7 1 1 1 5 5 5 5 5 5 7 7 7 7 7 7 3 3 3 3 1 1 1 1 1 1 3 3 дерево вариантов

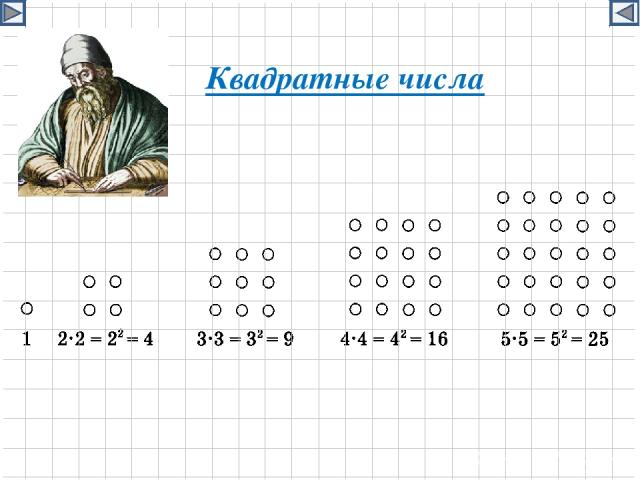
Квадратные числа

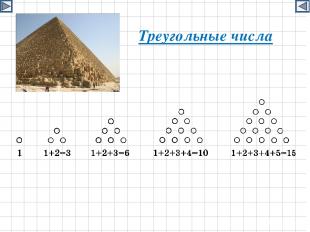
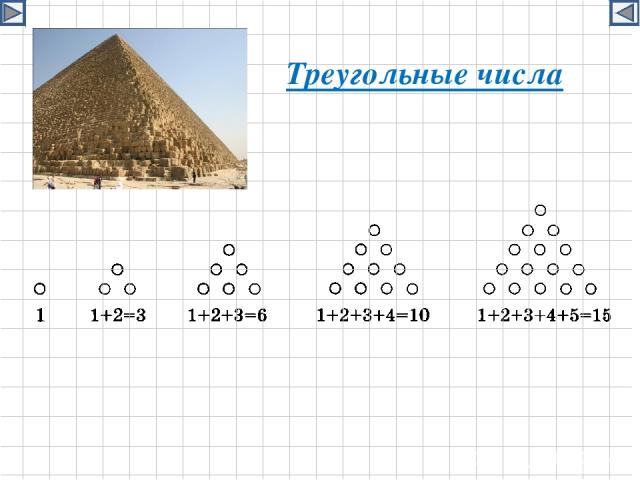
Треугольные числа

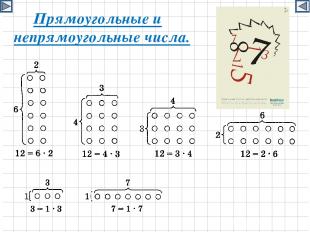
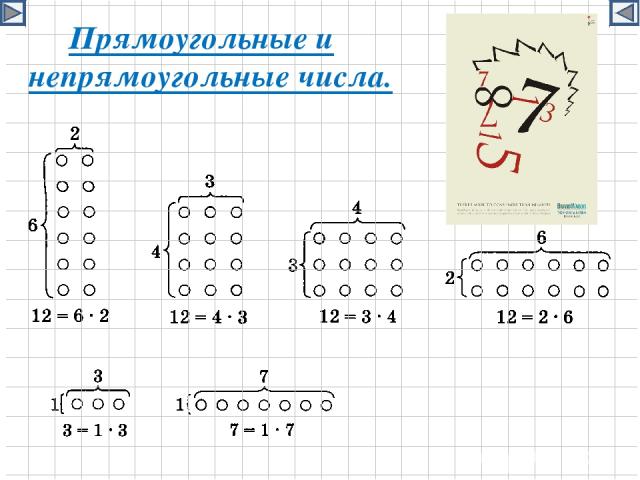
Прямоугольные и непрямоугольные числа.

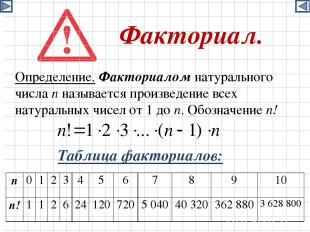
Факториал. Таблица факториалов: Определение. Факториалом натурального числа n называется произведение всех натуральных чисел от 1 до n. Обозначение n! n 0 1 2 3 4 5 6 7 8 9 10 n! 1 1 2 6 24 120 720 5 040 40 320 362 880 3 628 800

Перестановки. Определение. Перестановкой называется конечное множество, в котором установлен порядок элементов. Число всевозможных перестановок из n элементов вычисляется по формуле: Pn = n!

Пример 1. Сколькими способами могут быть расставлены восемь участниц финального забега на восьми беговых дорожках? Решение: P8 = 8! = 40 320

Пример 2. Сколько различных четырёхзначных чисел можно составить из цифр 0, 1, 2, 3, причём в каждом числе цифры должны быть разные? Решение: Р4 – Р3 = 4! – 3! = 18.

Пример 3. Имеется 10 различных книг, среди которых есть трёхтомник одного автора. Сколькими способами можно расставить эти книги на полке, если книги трёхтомника должны находиться вместе, но в любом прядке? Решение:

Размещения. Определение. Размещением из n элементов , называют конечного множества по k, где упорядоченное множество, состоящее из k элементов.

Пример 1. Из 12 учащихся нужно отобрать по одному человеку для участия в городских олимпиадах по математике, физике, истории и географии. Каждый из учащихся участвует только в одной олимпиаде. Сколькими способами это можно сделать? Решение:

Пример 2. Сколько существует семизначных телефонных номеров, в которых все цифры различны и первая цифра отлична от нуля? Решение:

Пример 3. Сколько существует трёхзначных чисел, составленных из цифр 1, 2, 3, 4, 5, 6 (без повторений), которые НЕ кратны 3? Решение:

Сочетания. Определение. Подмножества, составленные из n элементов данного множества и содержащие k элементов в каждом подмножестве, называют сочетаниями из n элементов по k. (Сочетания различаются только элементами, порядок их не важен: ab и ba – это одно и тоже сочетание).

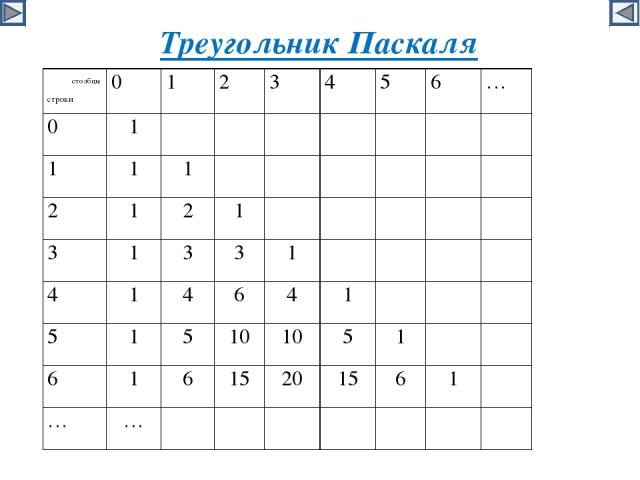
Треугольник Паскаля 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 … …

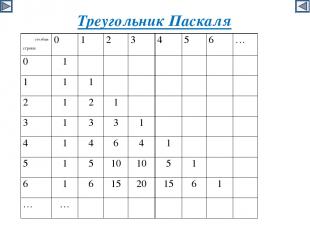
Треугольник Паскаля столбцы строки 0 1 2 3 4 5 6 … 0 1 1 1 1 2 1 2 1 3 1 3 3 1 4 1 4 6 4 1 5 1 5 10 10 5 1 6 1 6 15 20 15 6 1 … …

Треугольник Паскаля …

Пример 1. Сколькими способами можно выбрать трёх дежурных из класса, в котором 20 человек? Решение:

Пример 2. Из вазы с цветами, в которой стоят 10 красных гвоздик и 5 белых, выбирают 2 красные гвоздики и одну белую. Сколькими способами можно сделать такой выбор букета? Решение:

Пример 3. Семь огурцов и три помидора надо положить в два пакета так, чтобы в каждом пакете был хотя бы один помидор и чтобы овощей в пакетах было поровну. Сколькими способами это можно сделать? Решение:

Частота и вероятность. Определение. Частотой случайного события в серии испытаний называется отношение числа испытаний, в которых это событие наступило (благоприятные испытания), к числу всех испытаний. , где m – число испытаний с благоприятным исходом, n – число всех испытаний. Нахождение частоты предполагает, чтобы испытание было проведено фактически.

Частота и вероятность. Определение. Вероятностью события А называется отношение числа благоприятных для А исходов к числу всех равновозможных исходов. . Нахождение вероятности не требует, чтобы испытание проводилось в действительности.

Пример 1. В урне 10 одинаковых шаров разного цвета: 2 красных, 3 синих, 5 жёлтых. Шары тщательно перемешаны. Наугад выбирается один шар. Какова вероятность того, что вынутый шар окажется: а) красным; б) синим; в) жёлтым? Решение: а) б) в)

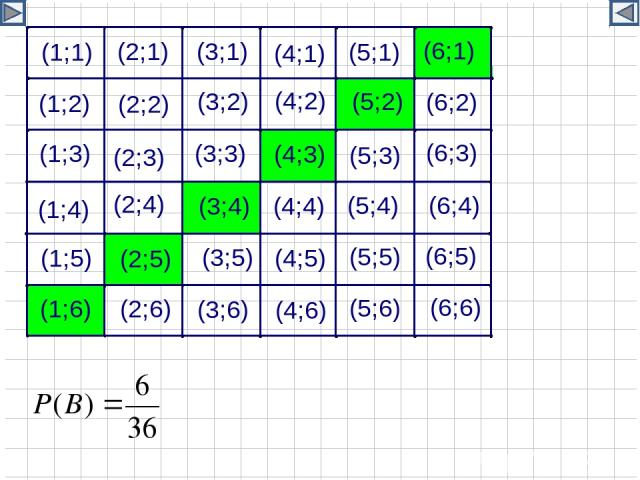
Пример 2. Коля и Миша бросают два игральных кубика. Они договорились, что если при бросании кубиков в сумме выпадет 8 очков, то выигрывает Коля, а если в сумме выпадет 7 очков, то выигрывает Миша. Справедлива ли эта игра?

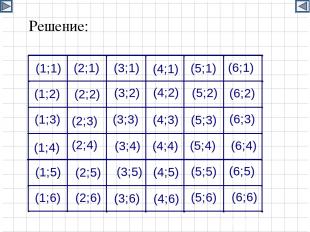
Решение:

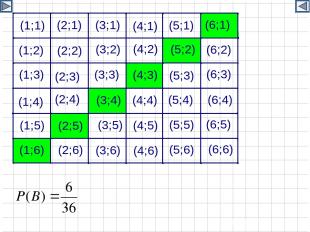
Пример 3. Из собранных 10 велосипедов только 7 не имеют дефектов. Какова вероятность того, что 4 выбранных велосипеда из этих 10 окажутся без дефекта? Решение:

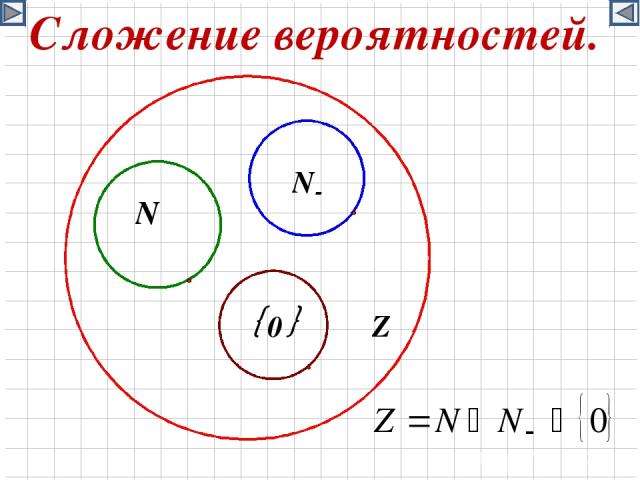
Сложение вероятностей.

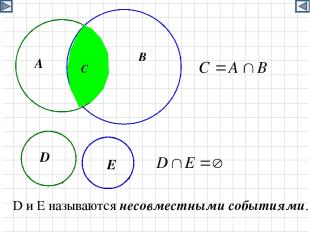
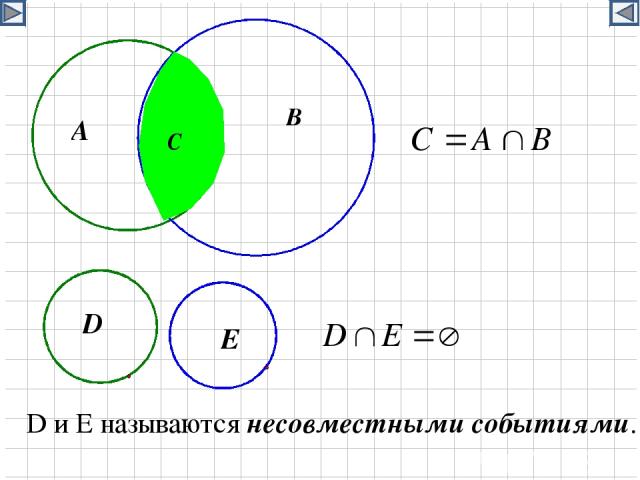
D и E называются несовместными событиями.

Сложение вероятностей. Вероятность наступления хотя бы одного из двух несовместных событий равна сумме их вероятностей.

Пример 1. В урне находятся 30 шаров 10 белых, 15 красных и 5 синих. Найдите вероятность появления цветного шара. Решение:

Пример 2. В контейнере 10 деталей, из низ 2 нестандартные. Найдите вероятность того, что из 6 наугад отобранных деталей окажется не более одной нестандартной. Решение: - всего событий Событие А – все 6 отобранных деталей стандартные, событие В – среди 6 отобранных деталей одна нестандартная.

- благоприятные события для А - благоприятные события для В

Умножение вероятностей. Вероятность совместного появления двух независимых событий равна произведению их вероятностей.

Пример 1. Монету бросают 3 раза подряд. Какова вероятность, что решка выпадет все три раза. Решение:

Пример 2. Вероятность попадания в цель при стрельбе из первого орудия равна 0,8, а при стрельбе из второго орудия равна 0,7. Найдите вероятность хотя бы одного попадания в цель, если каждое орудие сделало по одному выстрелу. Решение: событие А – попадание в цель 1-го орудия; событие В – попадание в цель 2-го орудия.

событие - промах 1-го орудия событие - промах 2-го орудия события и независимые события А и противоположные