Презентация на тему: «Производные» 10 класс алгебра

Применение производной к исследованию функций Производная и экстремумы. Исследование функций на монотонность. Урок в 10-3 классе. Учитель – Ирина Геннадьевна Рубцова МОУ лицей №18 г. Калининграда * 5klass.net

ТЕОРЕТИЧЕСКАЯ РАЗМИНКА Кое-что о свойствах функций. *

1.Закончите формулировки утверждений: А) функцию у=f(х) называют возрастающей на множестве ХC D(f), если для любых двух точек х1 и х2 множества Х, таких, что х1

2.Выберите верное утверждение: А) Точку х0 называют точкой максимума функции у=f(х), если для всех х≠х0 выполняется неравенство f(х)

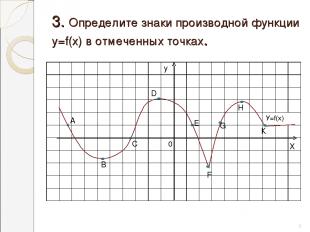
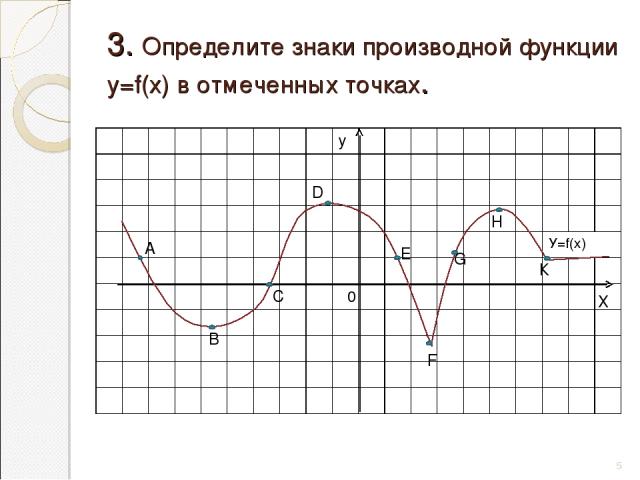
3. Определите знаки производной функции у=f(х) в отмеченных точках. * 0 В А С Е F G H К Х у D У=f(х)

1.Ответы: А) функцию у=f(х) называют возрастающей на множестве ХC D(f), если для любых двух точек х1 и х2 множества Х, таких, что х1

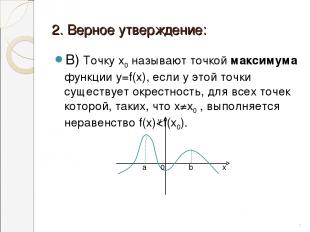
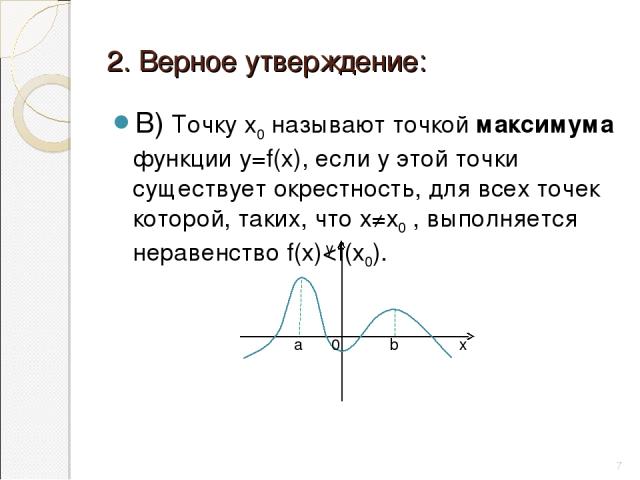
2. Верное утверждение: В) Точку х0 называют точкой максимума функции у=f(х), если у этой точки существует окрестность, для всех точек которой, таких, что х≠х0 , выполняется неравенство f(х)

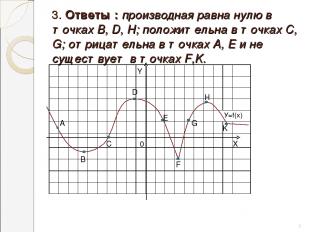
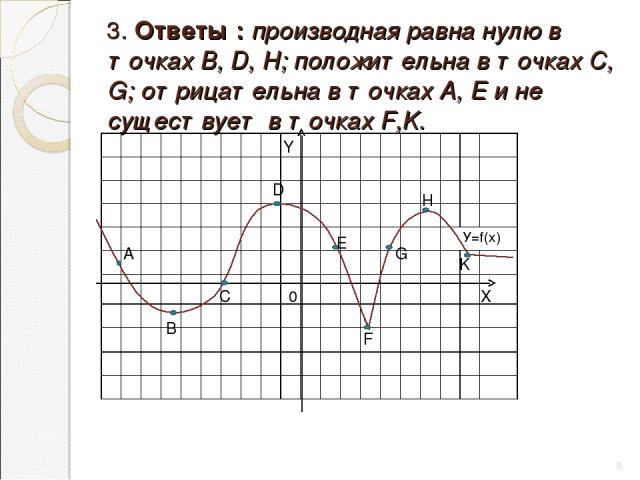
3. Ответы : производная равна нулю в точках В, D, Н; положительна в точках С, G; отрицательна в точках А, Е и не существует в точках F,K. * А В С D Е F G H K X Y 0 У=f(х)

ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ ДЛЯ ИССЛЕДОВАНИЯ ФУНКЦИЙ. Определенно, существует тесная связь между свойствами функции и ее производной. Но какая – предстоит найти. Итак, … *

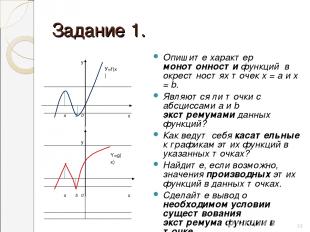
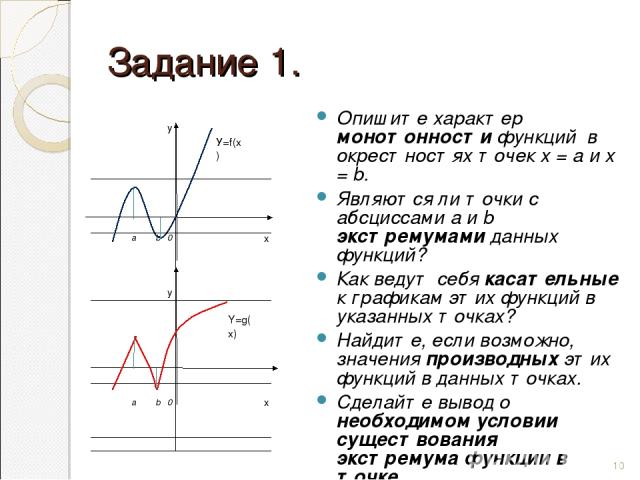
Задание 1. Опишите характер монотонности функций в окрестностях точек х = а и х = b. Являются ли точки с абсциссами а и b экстремумами данных функций? Как ведут себя касательные к графикам этих функций в указанных точках? Найдите, если возможно, значения производных этих функций в данных точках. Сделайте вывод о необходимом условии существования экстремума функции в точке. * y У=f(x) а b 0 x y Y=g(x) a b 0 x

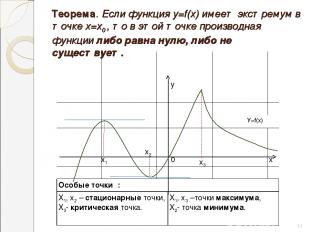
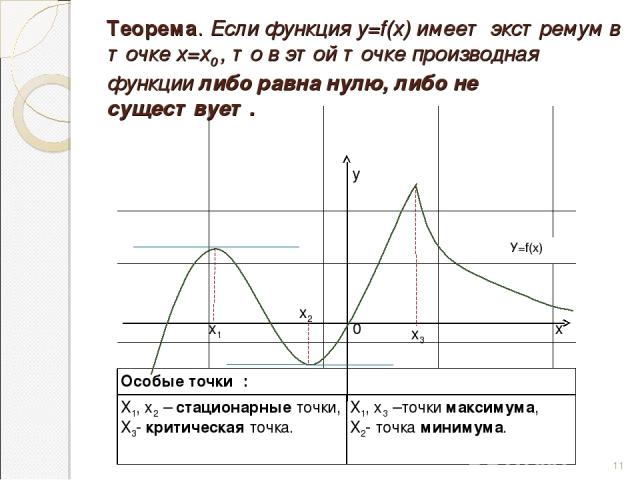
Теорема. Если функция у=f(х) имеет экстремум в точке х=х0 , то в этой точке производная функции либо равна нулю, либо не существует. у х2 х1 х3 х 0 * У=f(х) Особые точки : Х1, х2 – стационарные точки, Х3- критическая точка. Х1, х3 –точки максимума, Х2- точка минимума.

Новые термины: Стационарная точка – внутренняя точка области определения функции, в которых производная равна нулю. Критическая точка – внутренняя точка области определения функции, в которых функция непрерывна, но производная не существует. *

Задание 2. Найдите точки, в которых функция у = х3 - 3х + 1 может иметь экстремумы. Решение: f ‘(x)=3x2 - 3. f ‘(x) существует при всех значениях аргумента. f ‘(x)=0 при х=1 и х=-1. Эти точки могут быть точками экстремума. *

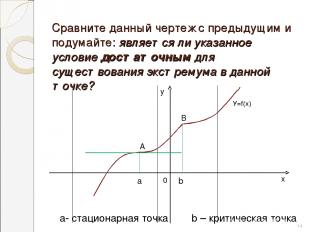
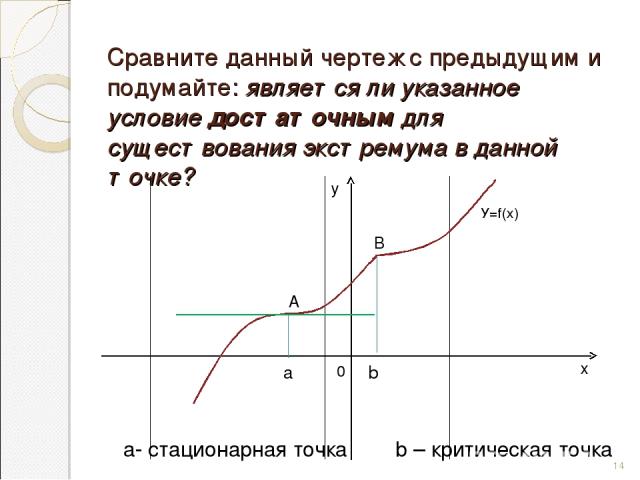
Сравните данный чертеж с предыдущим и подумайте: является ли указанное условие достаточным для существования экстремума в данной точке? А В а b 0 * а- стационарная точка b – критическая точка у У=f(х) х

Вывод: при переходе через точку экстремума характер монотонности функции меняется Вопрос: как связаны монотонность функции и производная? *

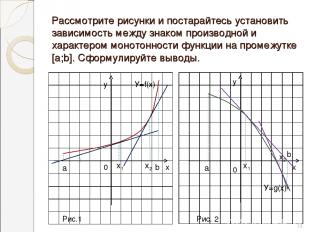
Рассмотрите рисунки и постарайтесь установить зависимость между знаком производной и характером монотонности функции на промежутке [a;b]. Сформулируйте выводы. у у х х 0 0 У=f(х) У=g(х) х1 х2 х1 х2 a b a b Рис.1 Рис. 2 *

Сравните свои выводы со следующим утверждением: Теорема. Если функция y=f(x) непрерывна на промежутке Х и ее производная положительна (соответственно отрицательна) во внутренних точках этого промежутка, то функция y=f(x) возрастает (соответственно убывает) на Х. *

Сравните формулировки теорем: Теорема. Если функция y=f(x) непрерывна на промежутке Х и ее производная положительна (соответственно отрицательна) во внутренних точках этого промежутка, то функция y=f(x) возрастает (соответственно убывает) на Х. Теорема. Если функция y=f(x) непрерывна на промежутке Х и ее производная неотрицательна (соответственно неположительна) во внутренних точках этого промежутка и равна нулю лишь в конечном множестве точек, то функция y=f(x) возрастает (соответственно убывает) на Х. *

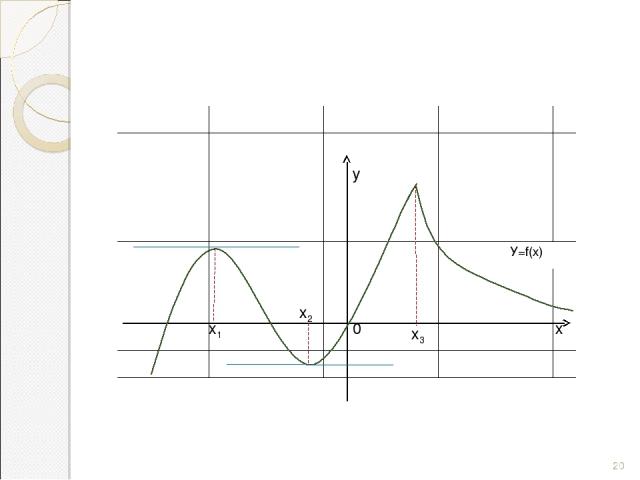
ОБОБЩАЕМ ИНФОРМАЦИЮ И ДЕЛАЕМ ВЫВОДЫ. Чтобы точка х=х0 была точкой экстремума функции, достаточно, чтобы: ………( ваше мнение?) *

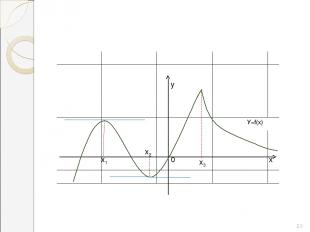
у х2 х1 х3 х 0 * У=f(х)

Теорема (достаточные условия экстремума). Пусть функция у=f(x) непрерывна на промежутке Х и имеет внутри промежутка стационарную или критическую точку х = х0. Тогда: а) если у этой точки существует такая окрестность, в которой при x0, то х=х0 – точка минимума функции у=f(x); б) если у этой точки существует такая окрестность, в которой при x0, а при x>x0 - неравенство f ‘(x)

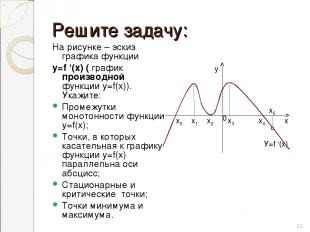
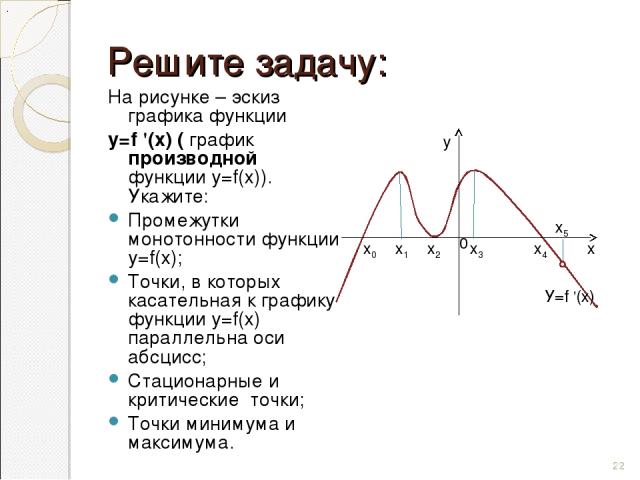
Решите задачу: На рисунке – эскиз графика функции у=f '(х) ( график производной функции у=f(х)). Укажите: Промежутки монотонности функции у=f(х); Точки, в которых касательная к графику функции у=f(х) параллельна оси абсцисс; Стационарные и критические точки; Точки минимума и максимума. х0 х1 х2 0 у х х3 х4 У=f '(х) * х5

Ответы : Функция возрастает на промежутках [x0;x2] и [x2;x4] Точки, в которых касательная к графику функции у=f(х) параллельна оси абсцисс: х0, х2, х4. Стационарные точки: х0, х2, х4. Критическая точка: х5; Точка минимума- х0, максимума – х4. х0 х1 х2 0 у х х3 х4 У=f '(х) * х5

Успехов! Спасибо за внимание! *