Презентация на тему: Алгебра «Производные»

Бессонова Т.Д. ВСОШ№7 Г.Мурманск 2008 5klass.net

Структура изучения темы Приращение аргумента, приращение функции Определение производной Нахождение производной по определению Формулы дифференцирования Уравнение касательной Геометрический смысл производной Механический смысл производной

Приращение функции ∆f и приращение аргумента ∆X х У f(x) x x+∆x f(x) f(x) f(x+∆x) ∆f f(x+∆x) α α

Определение производной Производной функции в данной точке называется предел отношения приращения функции в этой точке к приращению аргумента, когда приращение аргумента стремится к нулю.

Происхождение терминов

Алгоритм отыскания производной

Пример нахождения производной по определению

Формулы дифференцирования Функция производная Функция производная

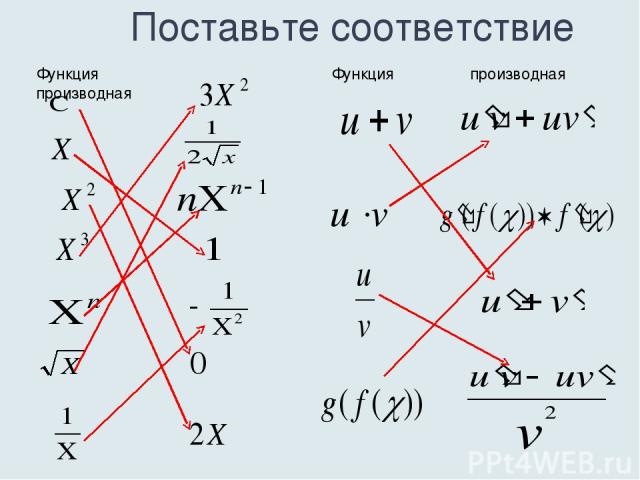
Поставьте соответствие Функция производная Функция производная

Найти производную функции Самостоятельная работа f(x) = х4 - 4х3 + 6х2 _ 7 f(x) = 7x5 – 9x3 +3x -3,5 f(x) = (x3 _ 2x)(x2 + 3) f(x) =

Ответы f’(x) = 4x3 – 12x2 + 12x f’(x) = 35x4 - 27x2 + 3 f’(x) = 5x4 + 3x2 - 6 f’(x) =

Критерии оценок «5» - без ошибок; «4» - 3 задания решены верно; «3» - 2 задания решены верно;

Касательная к графику функции x₀+∆x x₀

Геометрический смысл производной Геометрический смысл производной состоит в том, что значение производной функции y=f(x) в точке x0 равно угловому коэффициенту касательной к графику функции в точке с абсциссой x0 :
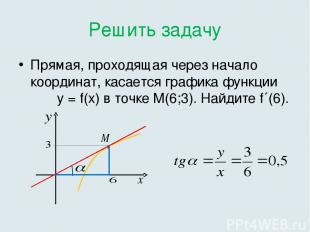
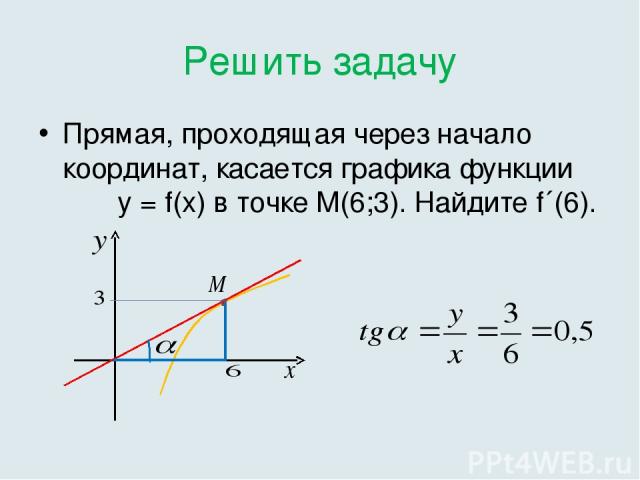
Решить задачу Прямая, проходящая через начало координат, касается графика функции у = f(x) в точке М(6;3). Найдите f´(6).
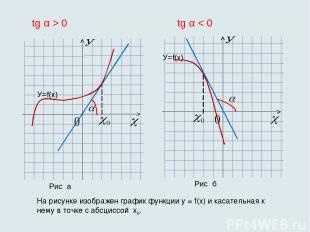
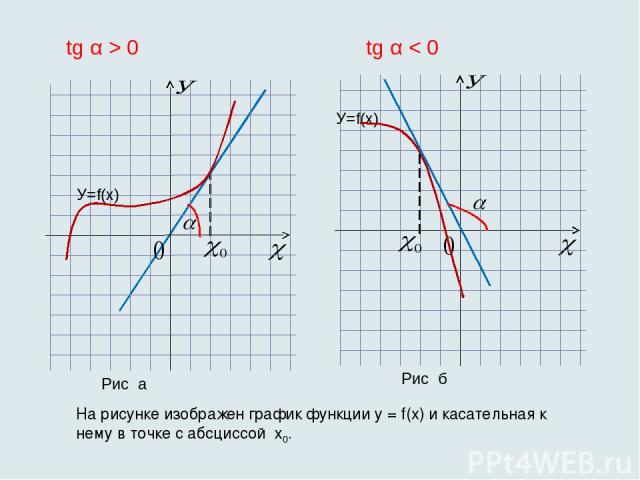
На рисунке изображен график функции у = f(x) и касательная к нему в точке с абсциссой х0. Рис а Рис б tg α > 0 tg α < 0

Уравнение касательной

Найти уравнение касательной к графику функции

Механический смысл производной

Точка движется прямолинейно по закону S(t) = 2 t ³ - 3 t Вычислите скорость движения точки: а) в момент времени t; б) в момент времени t=2с. Решение. а) б)

Задача №268 Материальная точка движется прямолинейно по закону х(t)=t³- 4t² Найдите скорость и ускорение в момент времени t=5с. (Перемещение измеряется в метрах)

Литература Мордкович А.Г. Алгебра и начала анализа. 10-11 класс.: В двух частях. Ч. 1:Учеб. для общеобразоват. учреждений.-6-е изд. – М: Мнемозина,2005. Алгебра и начала анализа: Учеб. Для 10-11 кл. общеобразоват. учреждений/ А.Н.Колмогоров, А.М.Абрамов, Ю.П. Дудницын и др.; Под ред. А.Н. Колмогорова. - М.: Просвещение, 2004.