Презентация на тему: «Числовые функции» 9 класс

Числовые функции 9 класс В реальной жизни мы говорим: «каковы мои функции» или «каковы мои функциональные обязанности», подразумевая «каков круг моих действий» или «что я должен сделать, как действовать». В реальной жизни слово «функция» означает «действие» или «правила действий». Тот же смысл имеет и математический термин «функция» 5klass.net

Определение функции Определение 1. Функцией называют такую зависимость переменной y от переменной х, при которой каждому значению переменной Х соответствует единственное значение переменной Y х - независимая переменная или аргумент функции, у - зависимая переменная или значение функции

Область определения функции Определение 2. Множество всех значений аргумента х называют областью определения функции и обозначают D(f) или D(y).

Область значений функции Определение 3. Множество всех значений функции у называют областью значений функции и обозначают E(y) или E(f).

Свойства функций Определение 4. Функцию y=f(x) называют возрастающей на промежутке, если большему значению аргумента соответствует большее значение функции х2 >Х1 f(х2) > f(х1). Монотонность

Определение 5. Функцию y=f(x) называют убывающей на промежутке, если большему значению аргумента соответствует меньшее значение функции х2 >Х1 f(х₁) < f(х₂). Монотонность

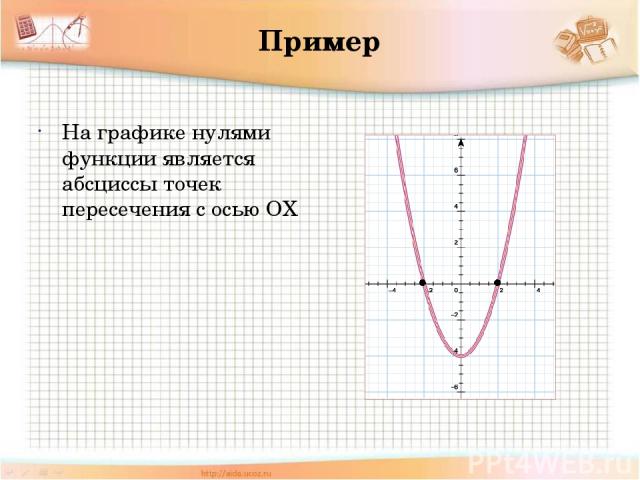
Нули функции Определение 6. Значение аргумента, при которых функция обращается в нуль, называют нулями функции
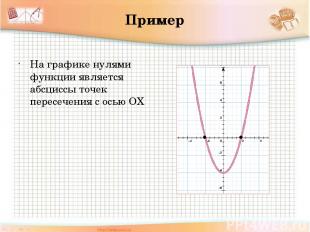
Пример На графике нулями функции является абсциссы точек пересечения с осью ОХ
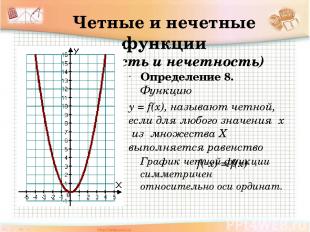
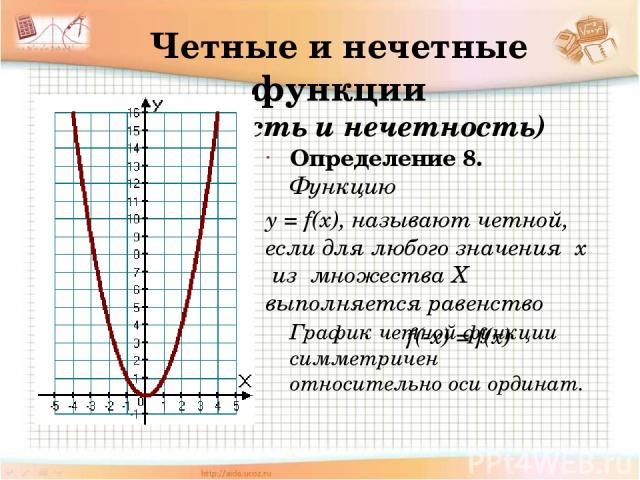
Четные и нечетные функции ( четность и нечетность) Определение 8. Функцию y = f(x), называют четной, если для любого значения х из множества Х выполняется равенство f(-x) = f(x) График четной функции симметричен относительно оси ординат.
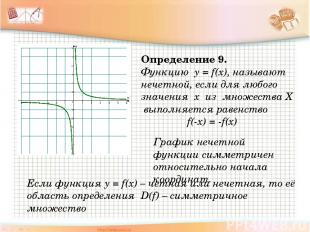
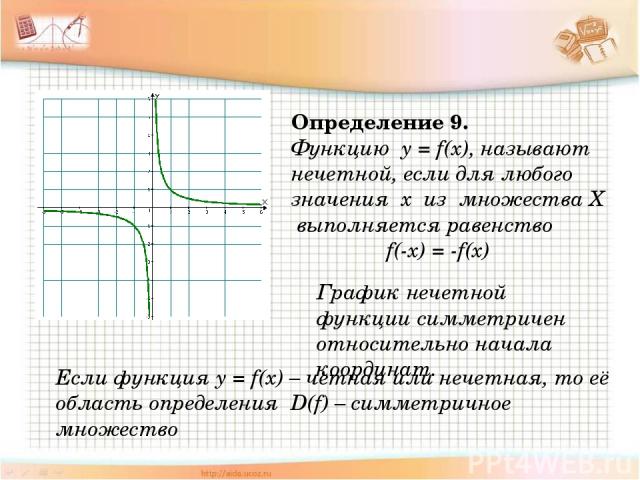
Определение 9. Функцию y = f(x), называют нечетной, если для любого значения х из множества Х выполняется равенство f(-x) = -f(x) График нечетной функции симметричен относительно начала координат. Если функция y = f(x) – четная или нечетная, то её область определения D(f) – симметричное множество