Презентация на тему: Теория вероятности в школе

Теория вероятностей для основной и средней школы 900igr.net

Теория вероятностей – математическая наука, изучающая закономерности случайных явлений. Знание закономерностей, которым подчиняются массовые случайные события, позволяет предвидеть, как эти события будут протекать. Методы теории вероятностей широко применяются в различных отраслях науки и техники: в теории надёжности, теории массового обслуживания, теоретической физике, геодезии, астрономии, теории ошибок, теории управления, теории связи и во многих других теоретических и прикладных науках. Теория вероятностей служит для обоснования математической статистики.

Испытанием называется реализация определенного комплекса условий, который может воспроизводиться неограниченное число раз.

Результатом испытания является событие. Конкретный результат испытания называется элементарным событием (исходом).

Сложным событием называется произвольное подмножество пространства элементарных событий.

Сложное событие в результате испытания наступает тогда и только тогда, когда в результате испытаний происходят все элементарные события, принадлежащее сложному.

Например: испытание - подбрасывание кубика. Элементарное событие - выпадение грани с номером “1”. Сложное событие - выпадение нечетной грани.

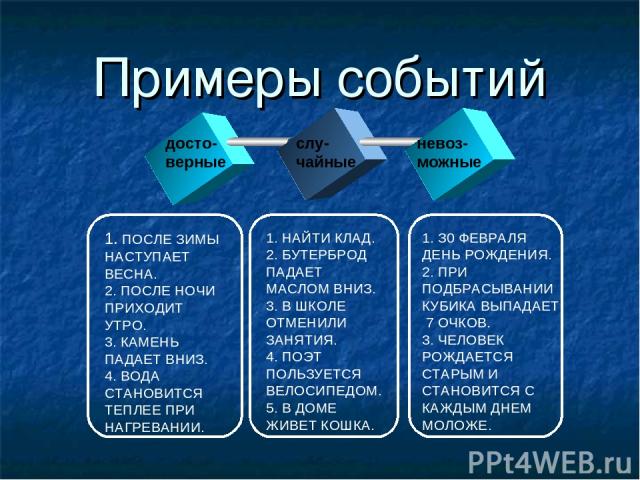
Событие бывает: - Достоверное (всегда происходит в результате испытания); - Невозможное (никогда не происходит); - Случайное (может произойти или не произойти в результате испытания).

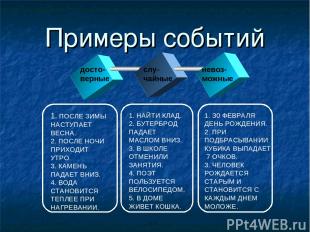
Примеры событий досто- верные слу- чайные невоз- можные 1. ПОСЛЕ ЗИМЫ НАСТУПАЕТ ВЕСНА. 2. ПОСЛЕ НОЧИ ПРИХОДИТ УТРО. 3. КАМЕНЬ ПАДАЕТ ВНИЗ. 4. ВОДА СТАНОВИТСЯ ТЕПЛЕЕ ПРИ НАГРЕВАНИИ. 1. НАЙТИ КЛАД. 2. БУТЕРБРОД ПАДАЕТ МАСЛОМ ВНИЗ. 3. В ШКОЛЕ ОТМЕНИЛИ ЗАНЯТИЯ. 4. ПОЭТ ПОЛЬЗУЕТСЯ ВЕЛОСИПЕДОМ. 5. В ДОМЕ ЖИВЕТ КОШКА. З0 ФЕВРАЛЯ ДЕНЬ РОЖДЕНИЯ. 2. ПРИ ПОДБРАСЫВАНИИ КУБИКА ВЫПАДАЕТ 7 ОЧКОВ. 3. ЧЕЛОВЕК РОЖДАЕТСЯ СТАРЫМ И СТАНОВИТСЯ С КАЖДЫМ ДНЕМ МОЛОЖЕ.

Определение вероятности. Вероятность события А — это отношение числа благоприятствующих этому событию исходов к общему числу несовместных элементарных исходов, которые образуют полную группу: P(A) = m / n, где m— число элементарных исходов, которые благоприятствуют А; n — число всех возможных элементарных исходов испытания.

Следовательно, можно записать следующие три свойства. 1. Вероятность достоверного события равна единице. Следовательно, если событие достоверно, то каждый элементарный исход испытания благоприятствует событию, тогда m = n, и Р(A) = m / n = n / n = 1. 2. Вероятность невозможного события равна нулю. Следовательно, если событие невозможно, то ни один из элементарных исходов испытания не благоприятствует событию, тогда m = 0, и Р (А) = m / n = 0 / n = 0. 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей. Следовательно, случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания, тогда 0 < m < n, стало быть, 0 < m / n < l, и 0 < Р (А) < 1 и 0≤ Р (А)≤ 1.

Противоположное событие По отношению к рассматриваемому событию А – это событие , которое не происходит, если А происходит. И наоборот. Например, событие А – «выпало четное число очков» и B – «выпало нечетное число очков» при бросании игрального кубика – противоположные. Теорема: Сумма вероятностей противоположных событий равна 1. Т.е.: или p+q=1. Пример: Вероятность того, что день будет дождливым p=0,7. Найти вероятность того, что день будет ясным. Решение: События «день будет дождливым» и «день будет ясным» противоположные. Поэтому искомая вероятность: q=1-p=1-0,7 = 0,3.

Типы событий События А и В называют совместными, если они могут произойти одновременно в одном испытании. События A и B называются несовместными, если они никогда не могут произойти в результате одного испытания.

Пример. А – «идет дождь», В – «на небе нет ни облачка» – несовместные. Пример. Коля и Саша играют в шашки. А – «Коля проиграл», В – «Саша выиграл», С – «Витя наблюдал за игрой» – совместные.

Действия над событиями 1. Событие C называется суммой A+B, если оно состоит из всех элементарных событий, входящих как в A, так и в B. На диаграмме Венна сумма А+В изображается: Если события А и В совместны, то сумма А+В означает, что наступает событие А, или событие В, или оба события вместе. Если события несовместны, то событие А+В заключается в том, что должны наступить только А или В, тогда + заменяется словом «или».

Теорема сложения вероятностей совместных событий. Теорема: Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления: Р(А+В)=Р(А)+Р(В) – Р(АВ) Пример: Вероятности попадания в цель при стрельбе первого и второго орудий соответственно равны р1=0,7 и р2=0,8. Найти вероятность попадания при одном залпе хотя бы одним из орудий. Решение: Вероятность попадания в цель каждым из орудий не зависит от результата стрельбы из другого орудия, поэтому события А (попадание первого орудия) и В (попадание второго орудия) независимы. Вероятность события А*В (оба орудия дали попадание) Р(А*В)=Р(А)*Р(В)=0,7*0,8=0,56 Искомая вероятность Р(А+В)=Р(А)+Р(В)-Р(АВ)=0,7+0,8-0,56=0,94

Данный пример можно было бы решить другим способом, используя формулу вероятности появления хотя бы одного события. Допустим, в результате испытания могут появиться 2 независимых в совокупности событий или некоторые из них. При этом вероятности появления каждого из этих событий даны. Для нахождения вероятности того, что наступит хотя бы одно из этих событий, воспользуемся следующей теоремой. Теорема. Вероятность появления хотя бы одного из событий A1 и А2, которые независимы в совокупности, равняется разности между единицей и произведением вероятностей противоположных событий : P(A) = 1—q1*q2.

Теорема сложения вероятностей несовместных событий Если события А и В несовместны, то событие А+В заключается в том, что должны наступить А или В, тогда + заменяется словом «или». Теорема: Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий: Р(А+В)=Р(А)+Р(В).

Пример: В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара. Решение: Появление цветного шара означает появление либо красного, либо синего шара. Соб. А – появление красного шара. Вероятность появления соб. А: Р(А)=10/30=1/3. Соб. В – появление синего шара. Вероятность появления соб. В: Р(В) = 5/30=1/6. События А и В несовместны (появление шара одного цвета исключает появление шара другого цвета), поэтому теорема сложения применима. Искомая вероятность: Р(А+В)= Р(А)+Р(В)= 1/3+1/6=1/2.

2. Событие C называется произведением A и B, если оно состоит из всех элементарных событий, входящих и в A, и в B (т.е. состоящие в совместном наступлении всех этих событий в результате испытания) На диаграмме Венна произведение изображается:

Пример. Пусть имеются следующие события: А – «из колоды карт вынута дама», В – «из колоды карт вынута карта пиковой масти». Значит, А*В означает «вынута дама пик». Пример. Бросается игральный кубик. Рассмотрим следующие события: А – « число выпавших очков < 5», В – «число выпавших очков > 2», С – «число выпавших очков четное». Тогда А*В*С – «выпало 4 очка».

Если случайное событие представлено как событие, которое при осуществлении совокупности условий S может произойти или не произойти, и если при вычислении вероятности события, кроме условий S, никаких других ограничений нет, то такая вероятность называется безусловной. Если же налагаются и другие дополнительные условия, то в таком случае вероятность события будет условной. Например, нередко подсчитывают вероятность события В при дополнительном условии, что совершилось событие А.

Вероятность события В, подсчитанная в предположении, что событие А уже наступило, называется условной вероятностью и обозначается Условная вероятность события В при условии, что событие А уже наступило вычисляется: = Р(А*В) / Р(А), если Р(А) > 0.

2. Теорема умножения вероятностей. Допустим известны вероятности Р(А) и двух событий А и В. Для нахождения вероятности того, что появится и событие А, и событие В можно воспользоваться теоремой умножения. Теорема. Вероятность совместного появления двух событий равняется произведению вероятности одного из них на условную вероятность другого, подсчитанную в догадке, что первое событие уже наступило: Р(А*В) = Р(А)*

Независимые события. Теорема умножения для независимых событий. Положим, что вероятность события В не зависит от появления события А. Событие В называется независимым от события А в том случае, если появление события А не меняет вероятности события В, другими словами, если условная вероятность события В равняется его безусловной вероятности: = Р(В). Теорема умножения Р(А*В) = Р(А)* для независимых событий выглядит следующим образом: Р(А*В) = Р(А)*Р(В).

Формула Бернулли

Если осуществляется несколько испытаний, к тому же вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания носят название независимых относительно события А. Событие А в различных независимых испытаниях может иметь или различные вероятности, или одну и ту же вероятность.

Допустим, делается n независимых испытаний. В каждом из них событие А может появиться или не появиться. Будем думать, что во всяком испытании вероятность события А одна и та же, равная р. Значит, вероятность того, что событие А не наступит в каждом испытании также постоянна, причем равна она q = 1—p. Пусть необходимо подсчитать вероятность того, что при n испытаниях событие А произойдет ровно k раз, а не осуществится (n — k) раз.

К примеру, если события А появилось 3 раза в четырех испытаниях, то допустимы следующие сложные события:

Таким образом, соответственно обозначает, что в первом, втором и третьем испытаниях событие А появилось, а в четвертом испытании оно не наступило.

Здесь под понимают искомую вероятность. К примеру, обозначает вероятность того, что в семи испытаниях событие появится ровно 2 раза, причем не наступит 5 раз. Искомую вероятность можно найти благодаря формуле Бернулли.

Формула Бернулли: где n – общее количество испытаний, к – количество наступивших испытаний.

Вероятность того, что в n испытаниях событие наступит менее k раз вычисляется по формуле:

Вероятность того, что в n испытаниях событие наступит более k раз вычисляется по формуле:

Вероятность того, что в n испытаниях событие наступит не менее k раз вычисляется по формуле:

Вероятность того, что в n испытаниях событие наступит не более k раз вычисляется по формуле:

Формула полной вероятности Вероятность события А, которое может наступить лишь при появлении одного из несовместных событий , образующих полную группу, равна сумме произведений вероятностей каждой из событий на соответствующую условную вероятность события А.

Формула полной вероятности где

Наивероятнейшее число появлений события в независимых испытаниях Наивероятнейшее число определяют из двойного неравенства:

Причем: а) если число np-q – дробное, то существует одно наивероятнейшее число ; б) если число np-q – целое, то существует два наивероятнейших числа, а именно и ; в) если число np – целое, то наивероятнейшее число = np

КОМБИНАТОРИКА

Термин «комбинаторика» происходит от латинского слова «combination» - соединение. Группы, составленные из каких-либо предметов (букв, шаров, кубиков и т.д.), называются соединениями.

КАК различить: задачи на перестановки или размещения (или сочетания)?

Перестановками из n элементов называются такие соединения, из которых каждое содержит все n элементов и которые отличаются друг от друга лишь порядком их расположения Размещениями из n элементов по k элементов называются такие соединения, состоящие из k элементов, взятых в определённом порядке из данных n элементов. (Порядок важен) Сочетаниями из n элементов по k называются такие соединения, составленные из k элементов, выбранных из данных n элементов. (Порядок не важен).

Рассмотрим три элемента а, b, с: Число размещений из 3 элементов по 2 ( ) – это ab, ac, ba, be, ca, cb. Число сочетаний из 3 элементов по 2 ( ) - это ab, ac, bc

СОЧЕТАНИЯ Несложные преобразования приводят полученную формулу к виду: Запомним 0!=1

СОЧЕТАНИЯ С ПОВТОРЕНИЯМИ

РАЗМЕЩЕНИЯ Краткая запись формулы

РАЗМЕЩЕНИЯ С ПОВТОРЕНИЯМИ

ПЕРЕСТАНОВКИ

ПЕРЕСТАНОВКИ С ПОВТОРЕНИЯМИ Пусть даны элементов первого типа, — второго типа, ... , — k-го типа, всего n элементов. Способы разместить их по различным местам называются перестановками с повторениями. Их количество обозначается Число перестановок с повторениями есть

Правило произведения Пусть требуется выполнить одно за другим k действий. При этом первое действие можно выполнить n1 способами, второе n2 способами и так до k-го действия. Тогда число m способов, которыми могут быть выполнены все k действий, по правилу произведения комбинаторики равно