Презентация на тему: Понятие производной функции

Работа Сизовой Натальи Владимировны МОУ «Лицей №3» г. Сарова Персональный идентификатор: 233-169-667 900igr.net

Автор Сизова Н. В., г. Саров Производная Автор Сизова Н. В., г. Саров

Тайны планетных орбит. Древнегреческие учёные умели решать немногие задачи кинематики – рассчитать либо равномерное прямолинейное движение, либо равномерное вращение вокруг оси. А планеты на небосводе двигались по самым замысловатым кривым . Свести эти движения планет к простым древним учёным не удавалось. Лишь в 17 веке немецкому учёному Иоганну Кеплеру удалось сформулировать законы движения планет. Оказалось, что планеты движутся по эллипсам, и притом неравномерно. Объяснить, почему это так, Кеплер не смог.

В конце 17 века Исаак Ньютон открыл законы динамики, сформулировал закон всемирного тяготения и развил математические методы, позволявшие сводить неравномерное к равномерному, неоднородное к однородному, криволинейное к прямолинейному. В основе лежала простая идея – движение любого тела за малый промежуток времени можно приближённо рассматривать как прямолинейное и равномерное. Одновременно с Ньютоном немецкий философ и математик Готфрид Вильгельм Лейбниц изучал, как проводить касательные к произвольным кривым.

Он также развил новое исчисление, которое оказалось по сути дела тождественным построенному Ньютоном. Обозначения, введённые Лейбницем, оказались настолько удачными, что сохранились и по сей день. Новая математика Ньютона и Лейбница состояла из двух больших частей – дифференциального и интегрального исчислений. В первом из них говорилось, как, изучая малую часть явления, сводить неравномерное к равномерному. Во второй – как из малых равномерных частей конструировать сложное неравномерное явление.

Повторение

Определение 1 Окрестностью точки называется интервал где δ – радиус окрестности. Определение 2 Функция называется бесконечно малой при ,если для любого ε > 0 существует проколотая окрестность точки а, на которой выполняется неравенство Определение 3 Число b называется пределом функции при , если , где - бесконечно малая функция при

Тема урока Понятие производной функции в точке

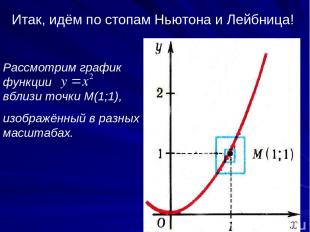
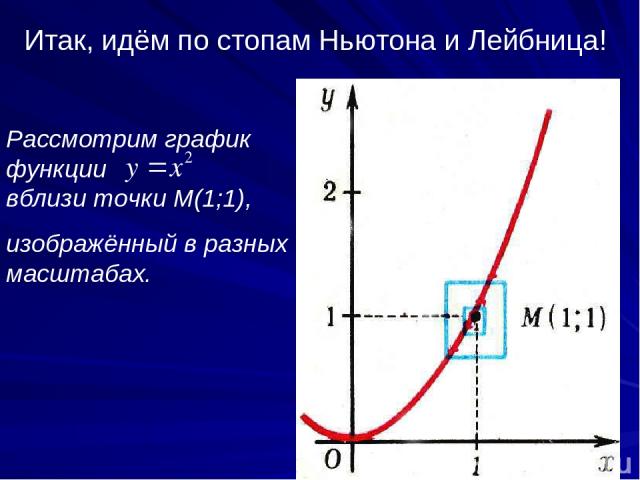
Итак, идём по стопам Ньютона и Лейбница! Рассмотрим график функции вблизи точки М(1;1), изображённый в разных масштабах.

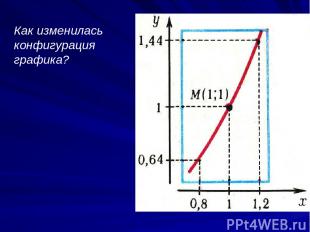
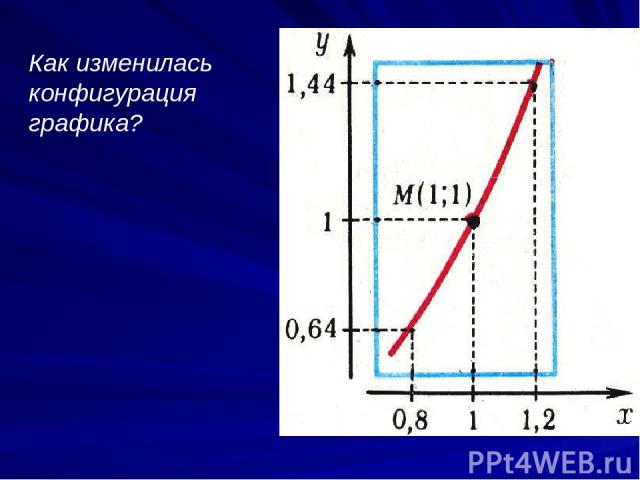
Как изменилась конфигурация графика?

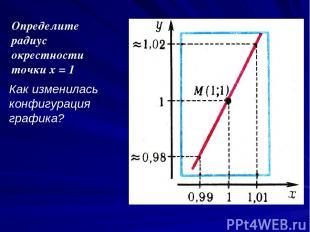
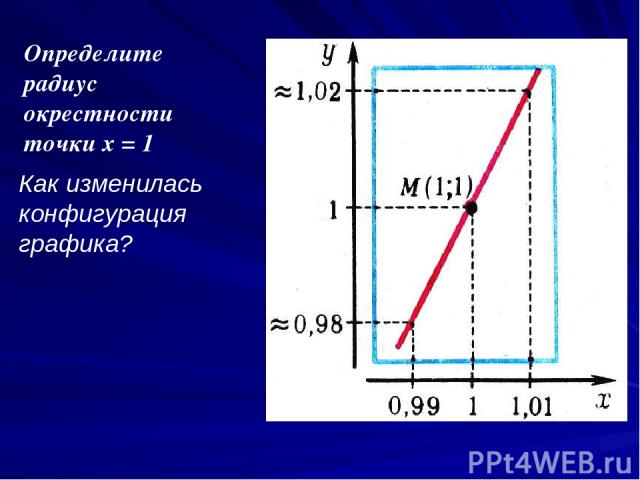
Определите радиус окрестности точки х = 1 Как изменилась конфигурация графика?

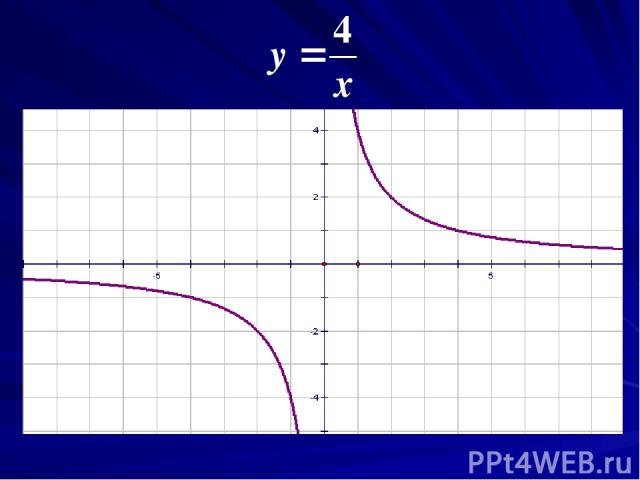
Существуют ли другие функции, графики которых обладают таким же свойством?

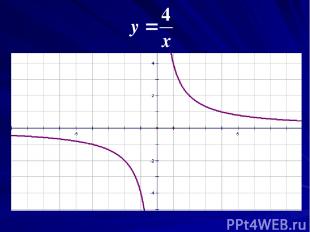
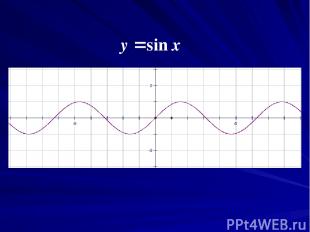
Основные выводы 1. Чем крупнее масштаб, тем меньше график функции будет отличаться от некоторой прямой, проходящей через точку М(1;1). 2. То же самое будет происходить с графиком функции вблизи любой другой точки. 3. Этим свойством обладают и многие другие кривые: окружность, гипербола, синусоида и т. д. Такое свойство функций называют «линейность в малом»

Cвойство «линейности в малом». Выразим это свойство на языке формул. Как перевести на математический язык слова «увеличить масштаб»? Радиус окрестности точки x0 уменьшается. х х0

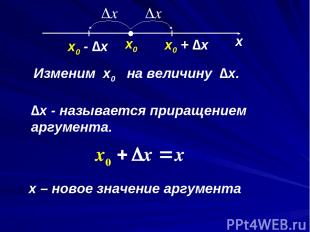
х х0 Изменим x0 на величину ∆x. ∆x - называется приращением аргумента. x0 + ∆x x0 - ∆x x – новое значение аргумента

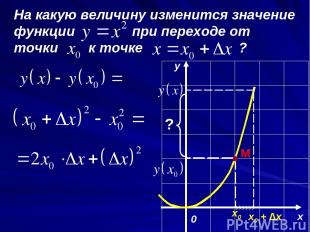
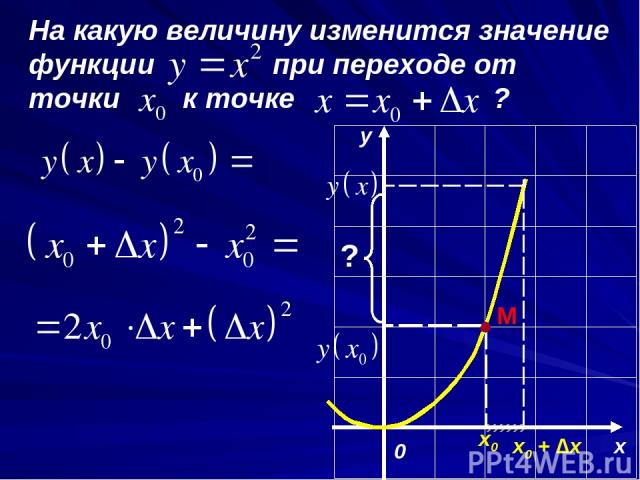
На какую величину изменится значение функции при переходе от точки к точке ? x y 0 х0 M х0 + ∆х ?

Величина y(x) – y(x0) называется приращением функции в точке x0 и обозначается ∆y(x0) .

Таким образом, чтобы вычислить приращение функции f(x) при переходе от точки x0 к точке x = x0 + Δx , нужно: 1. найти значение функции f(x0); 2. найти значение функции f(x0 + Δx) 3. найти разность f(x0 + Δx) – f(x0)

Почему график функции y = x2 «выпрямляется», если мы увеличиваем масштаб?

Найдите приращение функции y = x2 в точке x0 = 1 Как изменяется слагаемое (∆х)2 при приближении к точке х = 1? (∆х)2 стремится к нулю быстрее, чем ∆х . Следовательно, при малых значениях ∆х величиной (∆х)2 можно пренебречь, следовательно

т.к. С другой стороны Таким образом,

Чем меньше ∆x, тем теснее в точке М(1;1) парабола примыкает к прямой y = 2x – 1. Или, парабола касается прямой y = 2x – 1 в точке М. В этом и заключается причина «выпрямления» графика функции y = x2 при увеличении масштаба.

Рассмотрим приращения нескольких функций и выясним, есть ли закономерности в их структуре.

Найдите приращение функции в точке :

Заметим, что приращения рассмотренных нами функций можно представить в виде суммы двух слагаемых.

Функция Приращение функции

Определение Величина α пренебрежимо мала по сравнению с ∆х, если

Функция Приращение функции

Определение Функция y = f(x) называется дифференцируемой в точке x0 , если её приращение в этой точке можно представить в виде где α – пренебрежимо мала по сравнению с ∆х, А – некоторое действительное число.

Что такое коэффициент А?

Значит, где - б. м. ф. при по определению предела функции в точке. Выразим из равенства коэффициент А

Определение Производной функции y = f(x) в точке x0 называется предел отношения приращения функции в точке x0 к приращению аргумента при условии, что приращение аргумента стремится к нулю. Операция отыскания производной функции называется дифференцированием.

Рассмотрим пример из физики, который также приводит к понятию производной.

Пусть тело движется по закону Надо найти скорость движения на промежутке времени Если то

Используя определение, найдите производные функций в точке :

Чтобы найти производную функции в точке, надо: найти приращение функции в точке ; найти отношение приращения функции к приращению аргумента; вычислить предел полученного отношения при условии, что приращение аргумента стремится к нулю.

Найдите производные следующих функций в точке : Функция Производная

Что узнали на уроке? 1) Величина называется приращением функции в точке и обозначается 2) Функция называется дифференцируемой в точке если её приращение в этой точке можно представить в виде где α – пренебрежимо мала по сравнению с ∆х. 3) Производной функции в точке называется предел отношения приращения функции в точке к приращению аргумента при условии, что приращение аргумента стремиться к нулю. 4) Чтобы найти производную функции, надо: найти приращение функции в точке; найти отношение приращения функции к приращению аргумента; вычислить предел полученного отношения при условии, что приращение аргумента стремиться к нулю.