Презентация на тему: Понятие предела функции

Ведение в Математический анализ – часть математики, в которой функции и их обобщения изучаются с помощью пределов. § Понятие функции Основные понятия Пусть X,Y – множества произвольной природы. ОПРЕДЕЛЕНИЕ. Если x X поставлен в соответствие единственный элемент y Y, то говорят, что на множестве X задана функция (отображение) с множеством значений Y. Записывают: f: X   Y, y = f(x) (где f – закон, осуществляющий соответствие) Называют: X – область (множество) определения функции x (x X) – аргумент (независимая переменная) Y – область (множество) значений y (y Y) – зависимая переменная (функция) 900igr.net

СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ 1) словесный; 2) табличный; 3) графический; ОПРЕДЕЛЕНИЕ. Графиком функции y = f(x) называется геометрическое место точек плоскости с координатами (x; f(x)). График функции y = f(x) будем также называть «кривой y = f(x)». 4) аналитический: а) явное задание (т.е. формулой y = f(x) ) б) неявное задание (т.е. с помощью уравнения F(x,y)=0 ).

Классификация вещественных функций вещественного аргумента

ОСНОВНЫЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ: 1) степенные: y = xr (r ℝ) 2) показательные: y = ax (a > 0, a  1) 3) логарифмические: y = logax (a > 0, a  1) 4) тригонометрические: y = sinx, y = cosx, y = tgx, y = ctgx 5) обратные тригонометрические: y = arcsinx, y = arccosx, y = arctgx, y = arcctgx ОПРЕДЕЛЕНИЕ. Элементарной функцией называется функция, которая может быть задана одной формулой y = f(x), где f(x) – выражение, составленное из основных элементарных функций и действительных чисел с помощью конечного числа операций сложения, вычитания, умножения, деления и взятия функции от функции.

Многочленом степени n (полиномом, целой рациональной) называется функция вида Рациональной (дробной рациональной) функцией называют отношение двух многочленов Иррациональными функциями называют функции, полученные конечным числом арифметических операций над аргументом х и конечного числа композиций степенных функций с рациональным показателем.

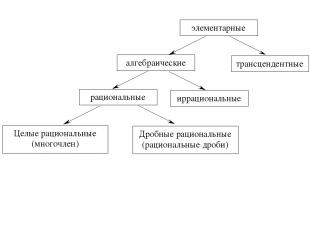
Алгебраическими функциями называют рациональные (целые рациональные и дробные рациональные) и иррациональные функции. Трансцендентными называют остальные элементарные функции.

Основные характеристики поведения функции 1) Четность функции (четная, нечетная, общего вида); 2) Периодичность функции; 3) Монотонность функции (возрастающая, убывающая, неубывающая, невозрастающая); 4) Ограниченность функции (ограниченная сверху, ограниченная снизу, ограниченная).

§ Предел функции Определение предела функции по Коши Пусть функция f(x) определена в некоторой окрестности точки x0 ℝ , кроме, может быть, самой точки x0 . U*(x0, ) = U(x0, ) \ {x0} – проколотая окрестность точки x0 . ОПРЕДЕЛЕНИЕ (по Коши, на языке - ). Число A ℝ называется пределом функции f(x) при x , стремящемся к x0 (пределом функции f(x) в точке x0), когда >0 >0 такое, что если x U*(x0, ) , то f(x) U(A, ) .

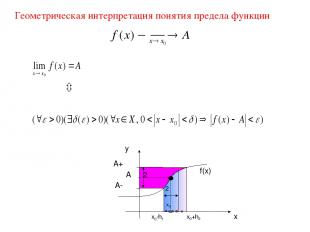
Геометрическая интерпретация понятия предела функции

Свойства пределов Если функция имеет предел при x   x0 , то этот предел единственный. 2) Если функция f(x) имеет предел при x   x0 , то она ограничена в некоторой проколотой окрестности точки x0 (говорят: функция локально ограничена).

ОПРЕДЕЛЕНИЕ. Функция (x) называется бесконечно малой при x   x0 , если 3) ЛЕММА (о роли бесконечно малых функций). Число A ℝ является пределом функции f(x) при x   x0  f(x) = A +  (x) , где (x) – бесконечно малая при x   x0 . 4) Пусть f(x) – ограничена в некоторой проколотой окрестности точки x0 , (x) – бесконечно малая при x   x0 . Тогда f(x)    (x)  – бесконечно малая при x   x0 .

5) Пусть f(x) и g(x) имеют предел при x   x0 . Тогда их сумма, разность, произведение и частное тоже имеют предел при x   x0 , причем Следствие свойства 5. Если f(x) имеет предел при x   x0 , то c ℝ функция с   f(x) тоже имеет предел при x   x0, причем Говорят: «константу можно вынести за знак предела». Замечание. Свойство 5 и его следствие обычно называют теоремами о пределах.

6) Пусть f(x) имеет предел при x   x0 и >0 такое, что f(x)   0 (или f(x) > 0), x U*(x0, ). Тогда 7) Пусть f(x) и g(x) имеют пределы при x   x0 и >0 такое, что f(x)   g(x) (или f(x) > g(x)), x U*(x0, ). Тогда 8) ЛЕММА (о двух милиционерах). Пусть f(x) и g(x) имеют одинаковый предел при x   x0 и >0 такое, что f(x)    (x)   g(x) , x U*(x0, ). Тогда функция (x) тоже имеет предел при x   x0 , причем

9) Пусть f: X   Y , : Y   Z и существуют пределы Тогда сложная функция (f(x)) имеет предел при x   x0 , причем Формула (1) называется формулой замены переменной в пределе.

Предел последовательности ОПРЕДЕЛЕНИЕ. Последовательностью называется функция, заданная на множестве натуральных чисел. Если область значений последовательности – числовое множество, то последовательность называют числовой, если область значений – множество функций, то последовательность называют функциональной.

Принято обозначать: аргумент последовательности: n (или k) значения функции: xn, yn и т.д. Называют: x1 – первый член последовательности, x2 – второй член последовательности и т.д. xn – n-й (общий) член последовательности. Способы задания последовательностей: 1) явно (т.е. формулой xn = f(n) ) 2) рекуррентным соотношением (т.е. формулой xn = F(xn-1, xn-2,…, xn-k) ) Записывают последовательность: { x1, x2, …, xn, …} – развернутая запись; { xn } – короткая запись (где xn  – общий член последовательности).

ОПРЕДЕЛЕНИЕ. Число a ℝ называется пределом последовательности { xn } если >0 N ℕ такое, что | xn – a | N. Записывают: Говорят: последовательность { xn } сходится (стремится) к a. Последовательность, имеющую предел, называют сходящейся (сходящейся к числу a) Последовательность, не имеющую предела, называют расходящейся.

ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ предела последовательности Пусть r ℝ, M(r) Ox M(r) – геометрическая интерпретация числа r ℝ . Пусть x0 ℝ, >0. Интервал (x0 –  ; x0 +  ) называют -окрестностью точки x0. (геометрическое определение -окрестности точки) Будем обозначать: U(x0, ) Имеем: U(x0, ) = {x ℝ :  |x – x0| 

Из определения предела последовательности следует: если {xn} a , то с геометрической точки зрения это означает, что в любой -окрестности точки a находятся все члены последовательности {xn}, за исключением, может быть, конечного числа членов этой последовательности. (Геометрическая интерпретация предела последовательности). a – точка «сгущения» последовательности { xn }.

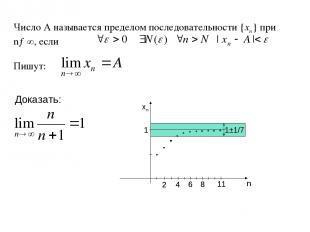
Число А называется пределом последовательности {xn} при n→∞, если Пишут: n xn 1 2 4 6 8 11 Доказать: 1±1/7 n 1 2 4 6 8 11

Последовательность {xn} называется бесконечно малой, если то есть если n xn 1 2 4 6 8 10 12 14 16 ε=0,2 ε=0,1 2ε 2ε

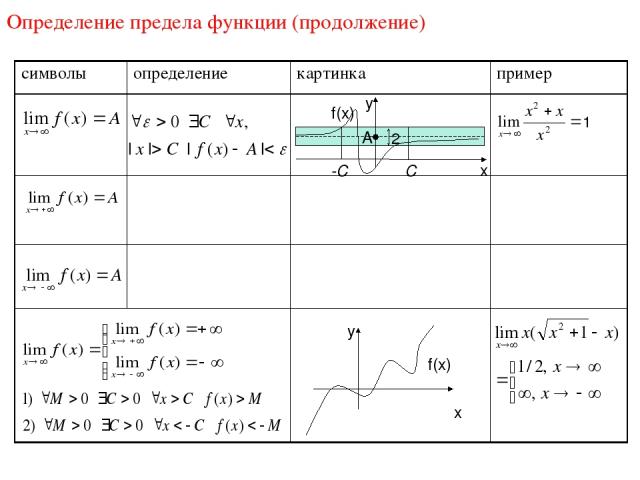
Бесконечно большие функции Пусть функция f(x) определена в некоторой окрестности точки x0 ℝ , кроме, может быть, самой точки x0 . ОПРЕДЕЛЕНИЕ (на языке - ). Функцию f(x) называют бесконечно большой при x   x0 (в точке x0), если M>0 >0 такое, что если x U*(x0, ), то | f(x) |>M . Говорят: «f(x) стремится к при x   x0» «предел функции f(x) при x   x0 равен ».

Частные случаи бесконечно больших функций: 1) f(x) – б.б. при x   x0 и f(x)   0 , x U*(x0, ) . Тогда | f(x) | = f(x) >M , x U*(x0, ) Записывают: Говорят: «f(x) стремится к +  при x   x0» «предел функции f(x) при x   x0 равен +  ». 2) f(x) – б.б. при x   x0 и f(x)   0 , x U*(x0, ). Тогда | f(x) | = – f(x) > M  f(x) 

СВОЙСТВА БЕСКОНЕЧНО БОЛЬШИХ ФУНКЦИЙ 1) Если f(x) – б.б. при x   x0, то функция 1/f(x) – б.м. при x   x0. Если (x) – б.м. при x x0, то функция 1/ (x) – б.б. при x x0. (связь бесконечно больших и бесконечно малых) 2) Если f(x) и g(x) – б.б функции одного знака, то их сумма f(x) + g(x) – б.б. того же знака. 3) Если f(x) – б.б при x   x0 , g(x) – ограниченна в некоторой окрестности U*(x0, ), то их сумма f(x) + g(x) – б.б. при x  x0. 4) Если f(x) и g(x) – б.б. при x   x0 , то их произведение f(x)   g(x) – тоже б.б. при x   x0 .

5) Если f(x) – б.б. при x   x0 , g(x) – имеет предел при x   x0, причем то их произведение f(x)   g(x) – б.б. при x   x0 . 6) Если f(x) – б.б. при x   x0 и x U*(x0, ) имеет место неравенство | f(x) | 0 такое, что f(x)    (x)   g(x) , x U*(x0, ). Тогда функция (x) тоже является б.б. того же знака при x   x0 . (лемма о двух милиционерах для б.б. функций)

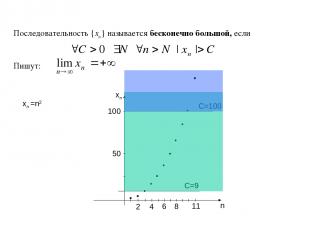
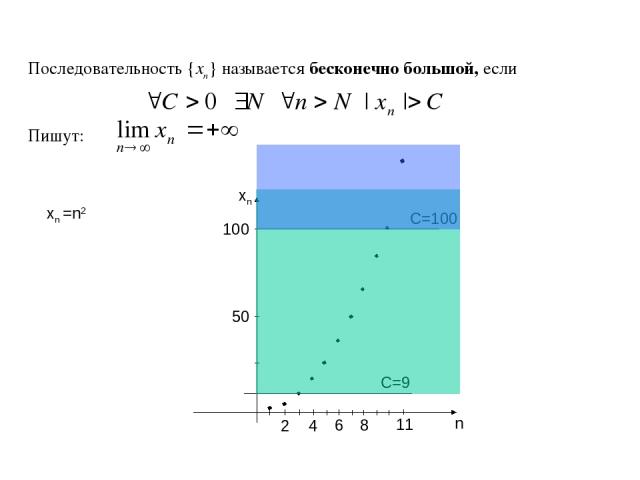
Последовательность {xn} называется бесконечно большой, если Пишут: n xn 100 50 2 4 6 xn =n2 8 C=9 C=100 11

Определение. Последовательность {xn} называется - возрастающей, если для любого n xn < xn+1; обозначают (↑) неубывающей, если для любого n xn ≤ xn+1; (↑) убывающей, если для любого n xn > xn+1; (↓) невозрастающей, если для любого n xn xn+1; (↓) Определение. Возрастающая и убывающая последовательности называются монотонными Теорема Вейерштрасса (о существовании предела монотонной последовательности) Если последовательность {xn} монотонно возрастает (убывает) и ограничена сверху (снизу), то у нее существует конечный предел, равный sup{xn} ( inf {xn} ). Предел монотонной последовательности

Односторонние пределы. Условие существования (x0 ℝ). Пусть f(x) определена в некоторой окрестности точки x0 ℝ , кроме, может быть, самой точки x0 . ОПРЕДЕЛЕНИЯ. 1) Число A ℝ называется пределом функции f(x) при x, стремящемся к x0 слева (в точке x0 слева), если >0 >0 такое, что если x удовлетворяет условию 0 0 такое, что если x удовлетворяет условию 0 

3) Говорят, что предел функции f(x) в точке x0 слева равен + (– ) (функция стремится к + (– ) при x, стремя- щемся к x0 слева), если M>0 >0 такое, что если x удовлетворяет условию 0 0 такое, что, если x удовлетворяет условию 0 

ТЕОРЕМА (необходимое и достаточное условие существования предела f(x) при x   x0  и x0 ℝ). Функция f(x) имеет предел (конечный) при x   x0 существуют конечные и равные между собой односторонние пределы функции f(x) при x   x0 . При этом Замечание. Все свойства пределов и бесконечно больших остаются справедливыми и для односторонних пределов.

Определение предела функции |2x+5-7|=2|x-1|

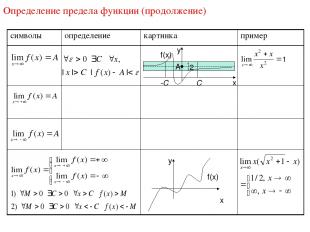
Определение предела функции (продолжение) 1 символы определение картинка пример

Замечательные пределы Название замечательных пределов в математическом анализе получили следующие два утверждения: – первый замечательный предел; – второй замечательный предел. СЛЕДСТВИЯ ПЕРВОГО ЗАМЕЧАТЕЛЬНОГО ПРЕДЕЛА

СЛЕДСТВИЯ ВТОРОГО ЗАМЕЧАТЕЛЬНОГО ПРЕДЕЛА Замечание. Из формулы замены переменной 1-й и 2-й замечательный пределы и их следствия остаются верными, если вместо x будет стоять любая б.м. функция (x).

Сравнение б.м. и б.б. функций Пусть функции (x) и (x) – б.м. при x   x0 . ОПРЕДЕЛЕНИЯ. 1) (x) называется бесконечно малой более высокого порядка чем (x) если Записывают: (x) = o( (x)) . 2) (x) и (x) называются бесконечно малыми одного порядка, если где С ℝ  и C   0 . Записывают: (x) = O( (x)) . 3) (x) и (x) называются эквивалентными, если Записывают: (x) ~  (x).

4) (x) называется бесконечно малой порядка k относи- тельно бесконечно малой (x), если бесконечно малые (x) и ( (x))k имеют один порядок, т.е. если где С ℝ  и C   0 . ТЕОРЕМА 6 (о замене бесконечно малых на эквивалентные). Пусть (x), (x), 1(x), 1(x) – б.м. при x   x0. Если (x) ~  1(x), (x) ~  1(x), то ТЕОРЕМА 7 (о главной части бесконечно малой). Пусть (x) и (x) – б.м. при x   x0, причем (x) – б.м. более высокого порядка чем (x). Тогда (x) =  (x) +  (x) ~  (x) . Б.м. (x) называют в этом случае главной частью бесконечно малой (x) .

Замечание. Из 1-го и 2-го замечательных пределов и их следствий можно получить таблицу эквивалентных бесконечно малых функций:

Аналогично бесконечно малым сравниваются и бесконечно большие функции. А именно, если f(x) и g(x) – бесконечно большие при x   x0, то 1) f(x) называется бесконечно большой более высокого порядка чем g(x) если 2) f(x) и g(x) называются бесконечно большими одного порядка, если где С ℝ  и C   0 ; 3) f(x) и g(x) называются эквивалентными бесконечно большими (записывают: f(x) ~ g(x)), если 4) f(x) называется бесконечно малой порядка k относительно бесконечно большой g(x), если где С ℝ и C   0 .

ТЕОРЕМА (о замене бесконечно больших на эквивалентные). Пусть f(x), g(x), f1(x), g1(x) – б.б. при x   x0. Если f(x) ~ f1(x) , g(x) ~ g1(x), то ТЕОРЕМА (о главной части бесконечно большой). Пусть f(x) и g(x) – б.б. при x   x0, причем g(x) – бесконечно большая более высокого порядка чем f(x). Тогда z(x) = f(x) + g(x) ~ g(x) . Б.б. g(x) называют в этом случае главной частью бесконечно большой z(x) .