Презентация на тему: Основы тригонометрии

Тригонометрия Тригонометрия-это часть геометрии, где с помощью тригонометрических функций связываются элементы треугольника. Тригонометрия-это объект математического анализа, где тригонометрические уравнения изучаются методами алгебры. 900igr.net

Этапы развития тригонометрии Тригонометрия в древности являлась вспомогательным разделом астрономии. Древнегреческие ученые разработали «тригонометрию хорд». Древнеиндийские ученые заменили хорды синусами. В VIII веке математики Востока превратили тригонометрию в самостоятельную математическую дисциплину. Ими были введены другие тригонометрические функции и составлены таблицы. Окончательный вид тригонометрия приобрела в XVIII веке в трудах Л.Эйлера.

Вопросы для повторения: Основные понятия Уравнения Неравенства Системы неравенств

Основные понятия тригонометрическая окружность градусы и радианы синус и косинус тангенс и котангенс

Тригонометрическая окружность 0 x y I II III IV

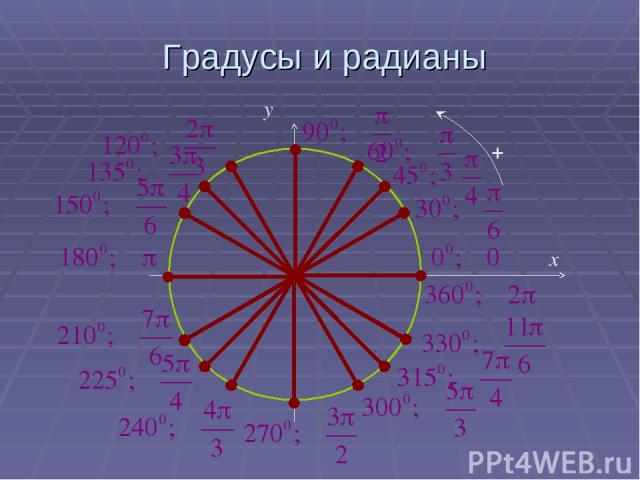
Градусы и радианы 0 x y

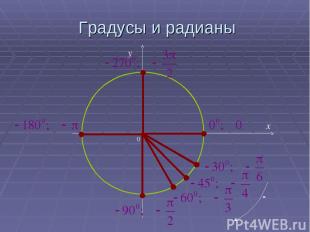
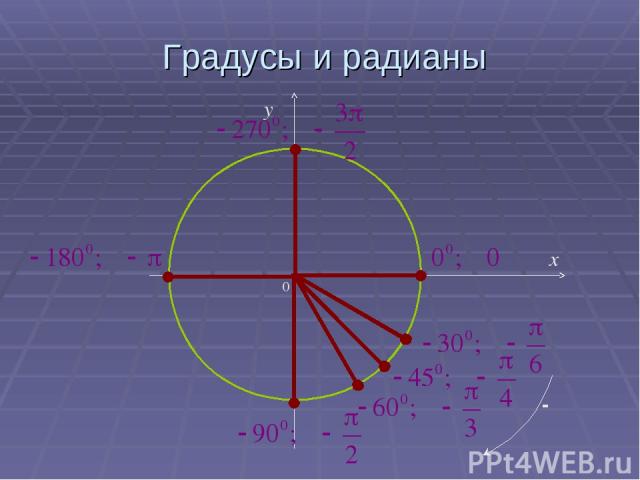
Градусы и радианы 0 x y

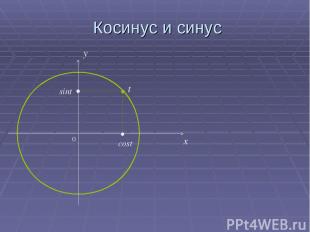
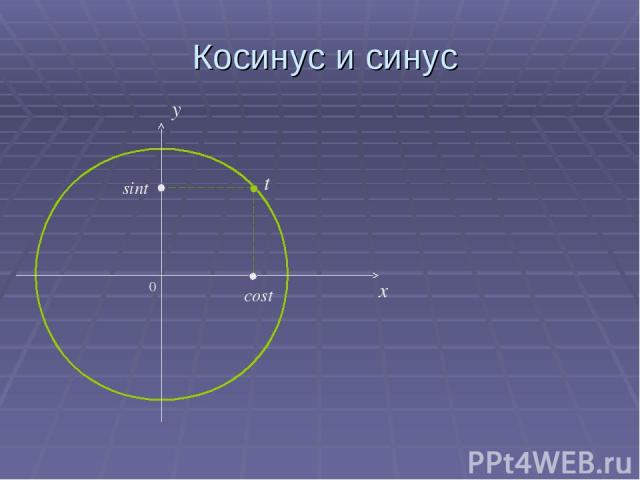
Косинус и синус 0 x y cost sint t

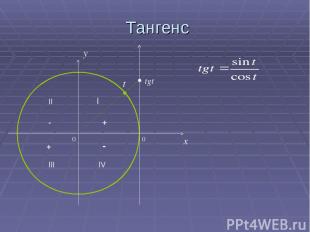
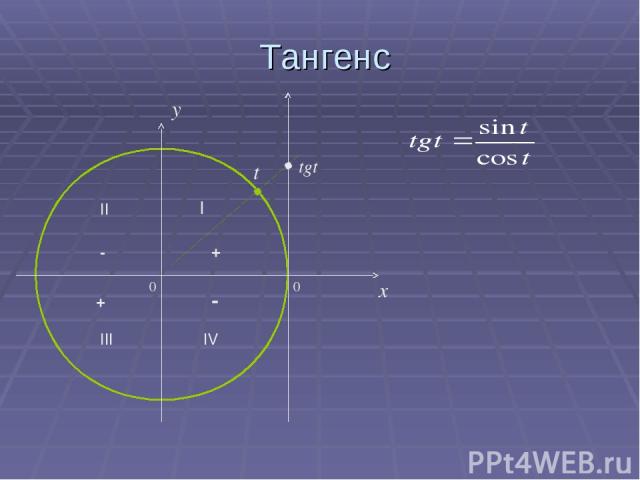
Тангенс 0 x y tgt t 0 II I III IV - - + +

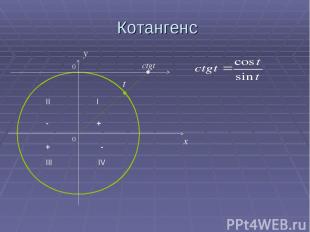
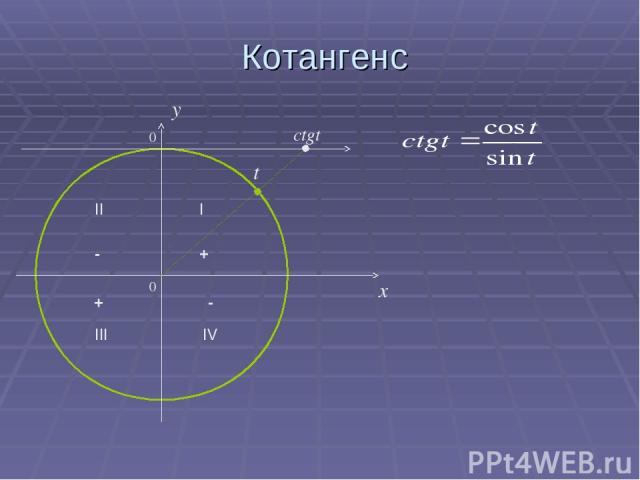
Котангенс 0 x y ctgt t 0 II I III IV - - + +

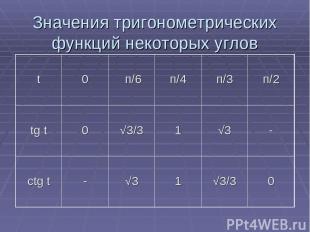
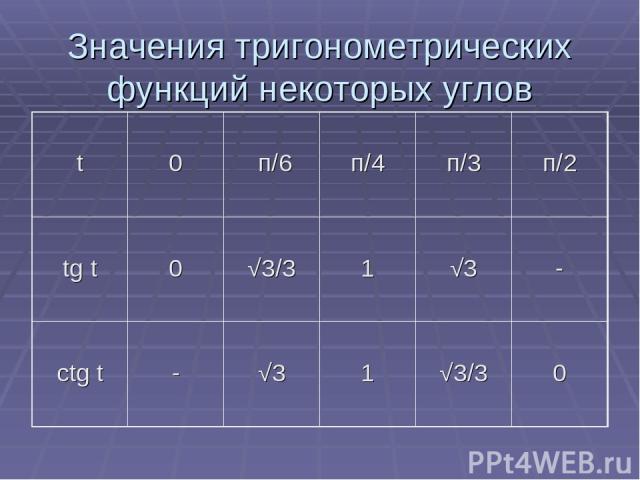
Значения тригонометрических функций некоторых углов t 0 п/6 п/4 п/3 п/2 tg t 0 √3/3 1 √3 - ctg t - √3 1 √3/3 0

Основные тригонометрические тождества sin2x+cos2x=1 tg t = sin t / cos t, где t≠ п/2+пк ctg t = cos t / sin t , где t≠ пк tg t ∙ ctg t = 1, где t≠ пк /2 1+tg2 t=1/cos2t, где t≠п/2+пк, к э Z 1+ctg2t=1/sin2t, где t≠ пк, к э Z

Тригонометрические функции углового аргумента а0=па/1800 рад. 10=п/1800 рад. 1 рад=1800 /п Угол в 1 радиан-это центральный угол, опирающийся на дугу длиной 1, длина которой равна радиусу окружности.

Уравнения cost = a sint = a

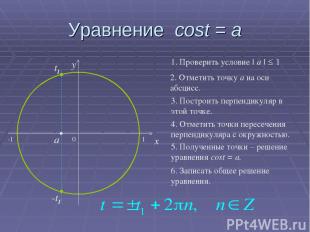
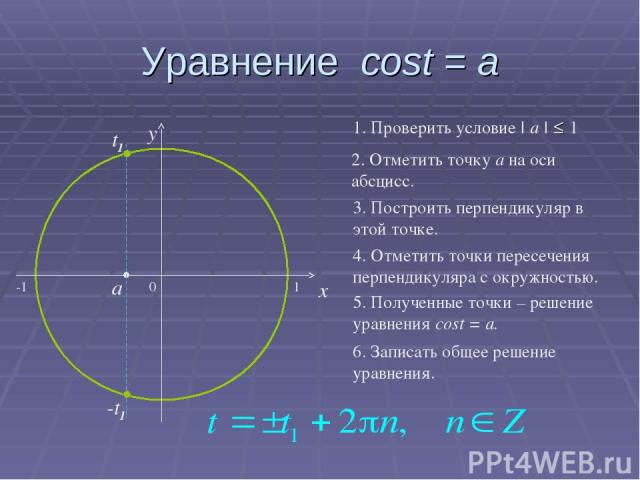
Уравнение cost = a 0 x y 2. Отметить точку а на оси абсцисс. 3. Построить перпендикуляр в этой точке. 4. Отметить точки пересечения перпендикуляра с окружностью. 5. Полученные точки – решение уравнения cost = a. 6. Записать общее решение уравнения. 1. Проверить условие | a | ≤ 1 a t1 -t1 -1 1

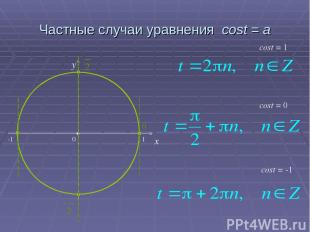
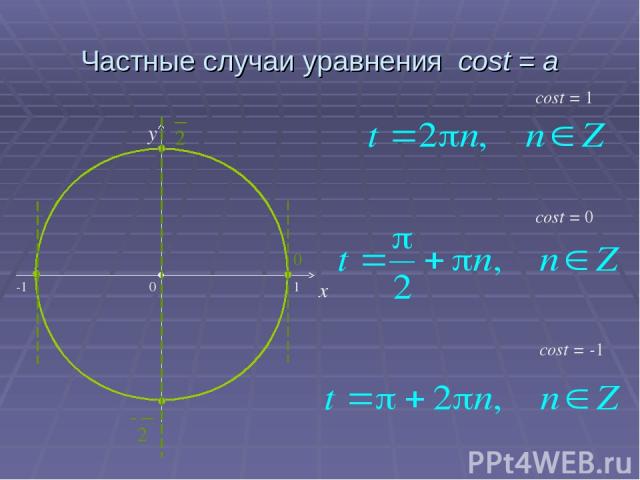
Частные случаи уравнения cost = a x y cost = 0 cost = -1 cost = 1

Уравнение sint = a 0 x y 2. Отметить точку а на оси ординат. 3. Построить перпендикуляр в этой точке. 4. Отметить точки пересечения перпендикуляра с окружностью. 5. Полученные точки – решение уравнения sint = a. 6. Записать общее решение уравнения. 1. Проверить условие | a | ≤ 1 a t1 π-t1 -1 1

Частные случаи уравнения sint = a x y sint = 0 sint = -1 sint = 1

Примеры уравнений 0 x y -1 1

Примеры уравнений 0 x y -1 1

Неравенства cost >a, cost ≤ a sint >a, sint ≤ a

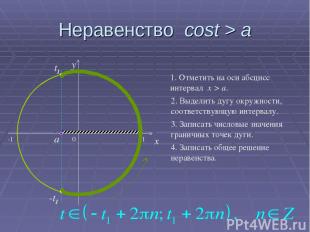
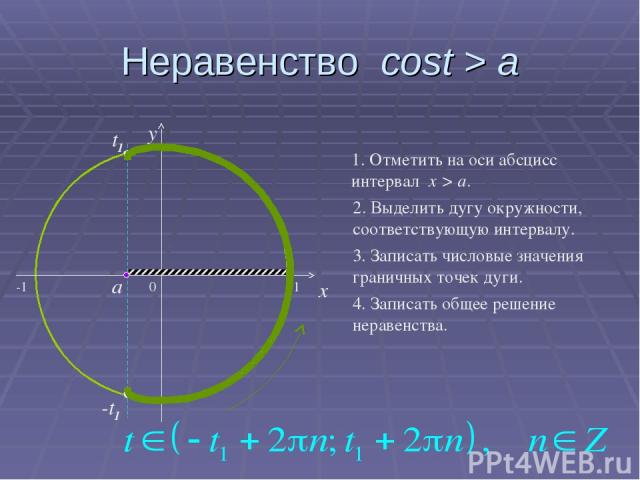
Неравенство cost > a 0 x y 1. Отметить на оси абсцисс интервал x > a. 2. Выделить дугу окружности, соответствующую интервалу. 3. Записать числовые значения граничных точек дуги. 4. Записать общее решение неравенства. a t1 -t1 -1 1

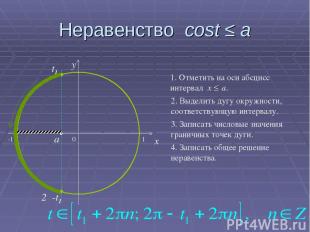
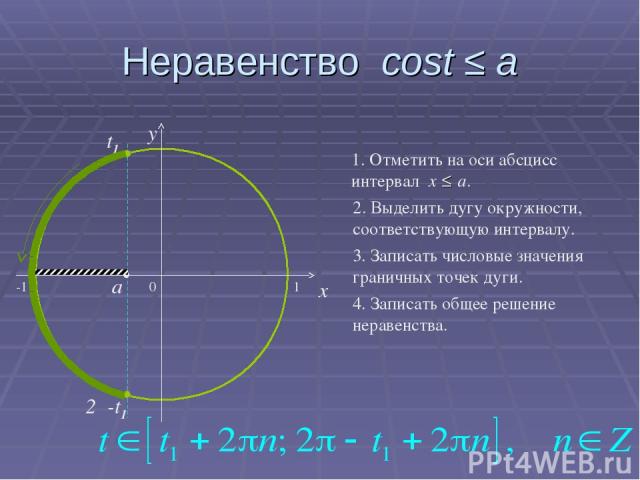
Неравенство cost ≤ a 0 x y 1. Отметить на оси абсцисс интервал x ≤ a. 2. Выделить дугу окружности, соответствующую интервалу. 3. Записать числовые значения граничных точек дуги. 4. Записать общее решение неравенства. a t1 2π-t1 -1 1

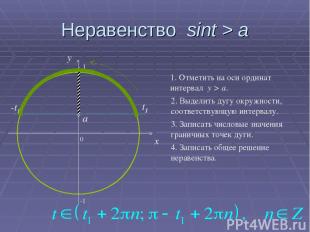
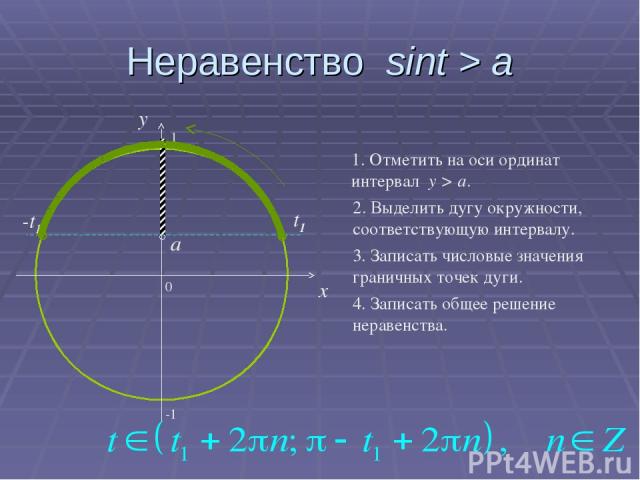
Неравенство sint > a 0 x y 1. Отметить на оси ординат интервал y > a. 2. Выделить дугу окружности, соответствующую интервалу. 3. Записать числовые значения граничных точек дуги. 4. Записать общее решение неравенства. a t1 π-t1 -1 1

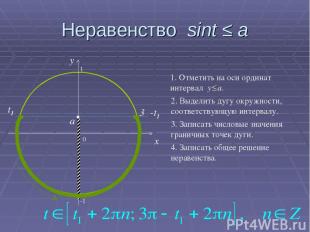
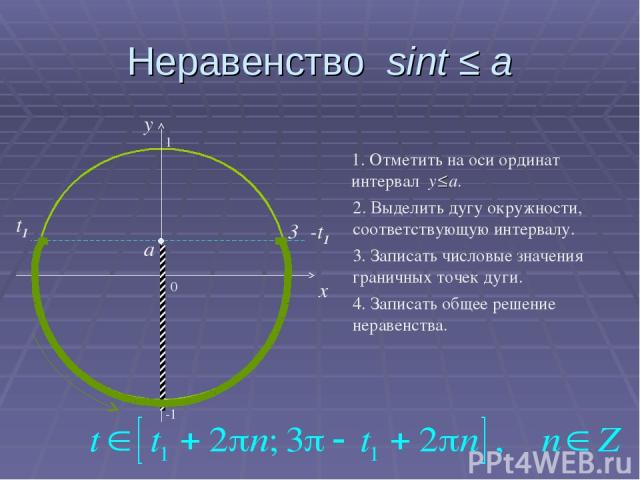
Неравенство sint ≤ a 0 x y 1. Отметить на оси ординат интервал y≤a. 2. Выделить дугу окружности, соответствующую интервалу. 3. Записать числовые значения граничных точек дуги. 4. Записать общее решение неравенства. a 3π-t1 t1 -1 1

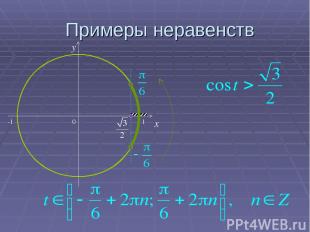
Примеры неравенств 0 x y -1 1

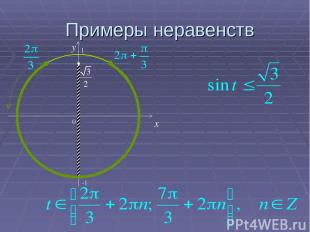
Примеры неравенств 0 x y -1 1

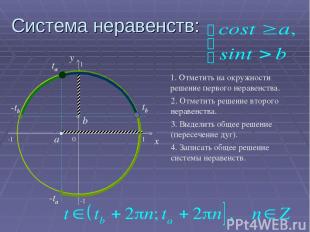
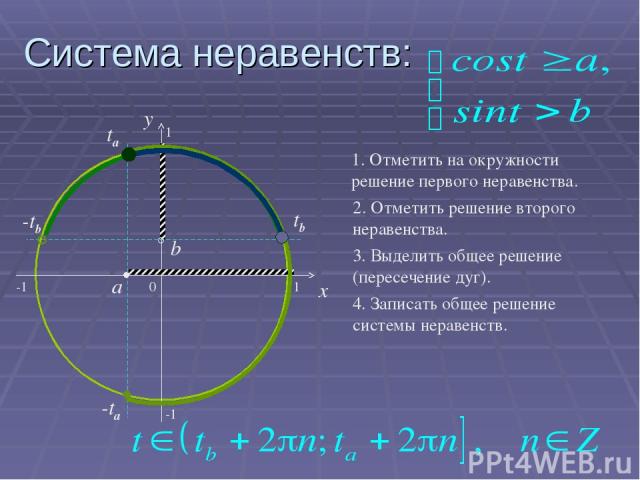
Система неравенств: 0 x y a ta -ta -1 1 b tb π-tb 1 -1 1. Отметить на окружности решение первого неравенства. 2. Отметить решение второго неравенства. 3. Выделить общее решение (пересечение дуг). 4. Записать общее решение системы неравенств.

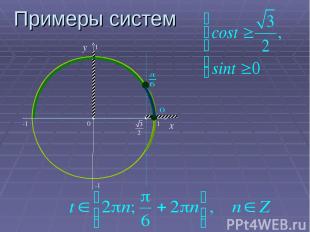
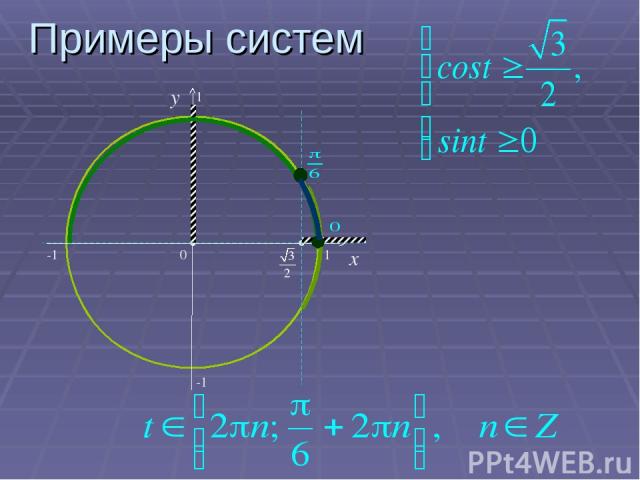
Примеры систем 0 x y -1 1 1 -1

Заключение Основные понятия тригонометрическая окружность градусы и радианы синус и косинус тангенс и котангенс Уравнения cost = a sint = a Неравенства cost >a, cost ≤ a sint >a, sint ≤ a Система неравенств