Презентация на тему: Неравенства (8 класс)

Конспект урока алгебры в 8 классе по теме: «Неравенства». Автор: Обухова Елена Александровна, учитель математики МОУ СОШ № 12 г. Сочи, Краснодарского края.2009 г.

Тип урока: обобщение.Цели урока: Образовательные: а). Обобщение и систематизация знаний учащихся по теме «Неравенства».б). Закрепление навыков решения тестовых заданий по данной теме. Развивающие: а). Формирование и развитие умения мыслить и анализировать.б). Развитие памяти.Воспитывающие: а). Воспитание умения работать самостоятельно.б). Воспитание умения выдерживать регламент времени, отведенного на решение каждого задания.в). Привитие интереса к предмету.

Повторение основных понятий.Новые термины математического языка. Линейное неравенство – неравенство вида ах+в>0 (ах+в<0), где а и в – любые числа, за исключением: а≠0.Квадратное неравенство – неравенство вида ах2+вх+с>0 (ах2+вх +с<0), где а≠0.

Основные правила решения неравенств. Правило 1. Любой член неравенства можно перенести из одной части неравенства в другую с противоположным знаком, не изменив при этом знак неравенства.Правило 2. Обе части неравенства можно умножить или разделить на одно и то же положительное число, не изменив при этом знак неравенства.

Основные правила решения неравенств. Правило 3. Обе части неравенства можно умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный.

Алгоритм решения квадратного неравенства. Найти корни квадратного трехчлена ах2+вх+с.Отметить найденные корни на оси Х и определить, куда (вверх или вниз) направлены ветви параболы, служащей графиком функции у=ах2+вх+с; сделать набросок графика.С помощью полученной геометрической модели определить, на каких промежутках оси Х ординаты графика положительны (отрицательны); включить эти промежутки в ответ.

Решение квадратных неравенств методом интервалов. Разложить квадратный трехчлен на множители, воспользовавшись формулой ах2+вх+с=а(х-х1)(х-х2).Отметить на числовой прямой корни трехчлена.Определить на каких промежутках трехчлен имеет положительный или отрицательный знак.Учитывая знак неравенства, включить нужные промежутки в ответ.

Вспомним как решать: №1. Известно, что 0<a<b. Какое из следующих чисел положительно?2а - 2в(а+3)·(-в)в - а 104) (а-5в)·а №2. На координатной прямой отмечены числа а, в и с. Какое из приведенных утверждений об этих числах неверно?b – c > 0a + b < 0ba > 0abc < 0

Вспомним как решать: №3. Решите линейное неравенство:3х – 5 ≥ 7х - 153х – 7х ≥ -15 + 5-4х ≥ -104х ≤ 10х ≤ 2,5Ответ: (-∞; 2,5]. Перенесите слагаемые, не забыв поменять знаки слагаемых 2. Приведите подобные слагаемыев левой и в правой частях неравенства. 3. Умножьте обе части на -1, не забыв поменять знак неравенства.

Вспомним как решать: №4. Решите неравенство методом интервалов:а) х2>16 б) х2+5>0 х2-16>0 Ответ: верно при(х-4)(х+4)>0 любом значении Х.+ - + в) х2+ 5<0 -4 4 х Ответ: не имеет Ответ:(-∞;-4)U(4;+∞) решений.

Вспомним как решать: №5. Решите квадратное неравенство:х2+7х-8<0 Как найти х1,2?х1=1; х2=-8. 1) + + 2) х1+х2=-в; х1х2=с -8 - 1 х 3) Если а+в+с=0, то Ответ: (-8; 1) х1=1; х2=с

Самостоятельная работа.Выполните тест:

А2. Из указанных неравенств выберите верное:

А3. Решите неравенство:

А5. Решите неравенство:

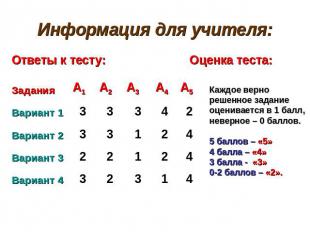
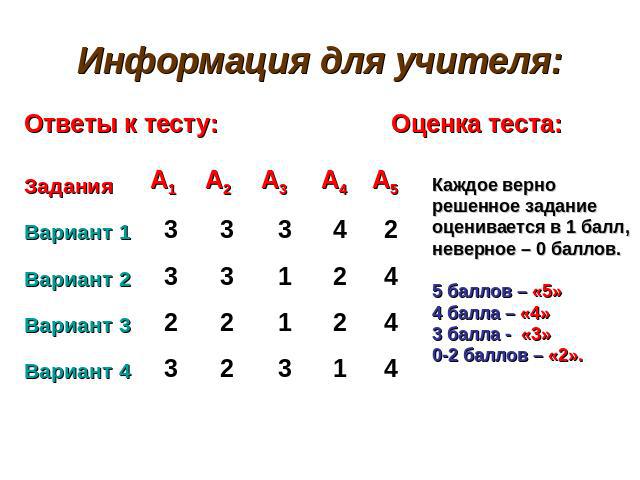
Информация для учителя: Ответы к тесту: Оценка теста: Каждое верно решенное задание оценивается в 1 балл, неверное – 0 баллов.5 баллов – «5»4 балла – «4»3 балла - «3»0-2 баллов – «2».

Используемая литература: «Алгебра 8 класс», часть 1, учебник, под редакцией А.Г. Мордковича, Мнемозина, 2007 г.«Алгебра 8 класс», часть 2, задачник, под редакцией А.Г. Мордковича, Мнемозина, 2007 г.«Тематический сборник тестовых заданий по алгебре для подготовки к государственной (итоговой) аттестации в новой форме», базовый уровень, под редакцией Е.А. Семенко, Просвещение-Юг, Краснодар, 2008 г.«Экзаменационные тестовые задания», Федеральная служба по надзору в сфере образования и науки РФ, 2008 г.«Краевые диагностические работы по алгебре в 9 классе», Департамент образования и науки Краснодарского края, ККИДППО, 2008 г.