Презентация на тему: Движения графиков функций

Движения графиков функций

Рассмотрим некоторые виды движения графиков функций. Пусть y=f(x) – исходная функция. f(x) f(x + а) f(x) f(x) + bf(x) - f(x) f(x) f( x ) f(x) f(x) Задания для самостоятельной работы

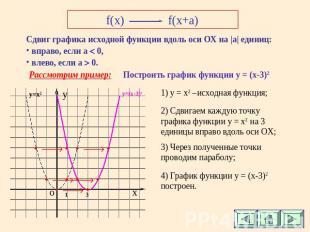
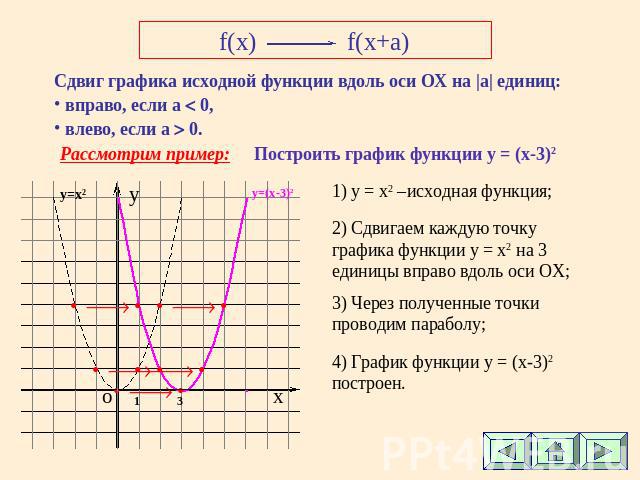
f(x)f(x+a) Сдвиг графика исходной функции вдоль оси ОХ на |а| единиц: вправо, если а 0, влево, если а 0. Построить график функции у = (x-3)2 1) y = x2 –исходная функция; 2) Сдвигаем каждую точку графика функции у = x2 на 3 единицы вправо вдоль оси ОХ; 3) Через полученные точки проводим параболу; 4) График функции у = (x-3)2 построен.

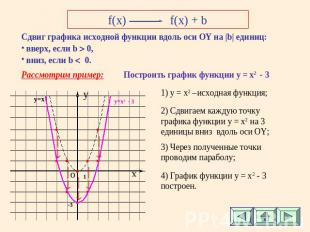
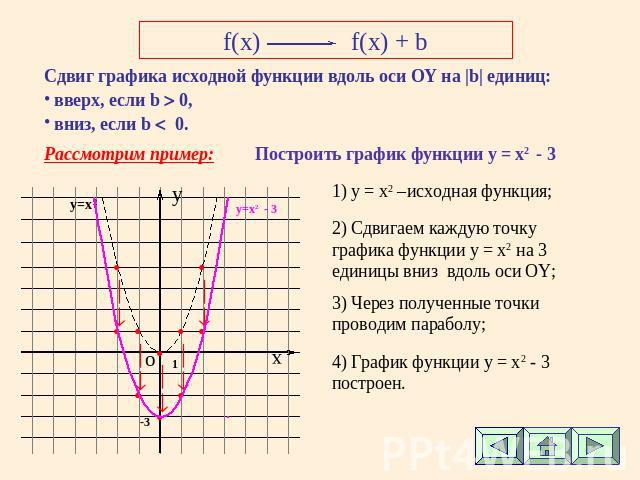
f(x)f(x) + b Сдвиг графика исходной функции вдоль оси ОY на |b| единиц: вверх, если b 0, вниз, если b 0. Рассмотрим пример: Построить график функции у = x2 - 3 1) y = x2 –исходная функция; 2) Сдвигаем каждую точку графика функции у = x2 на 3 единицы вниз вдоль оси ОY; 3) Через полученные точки проводим параболу; 4) График функции у = x2 - 3 построен.

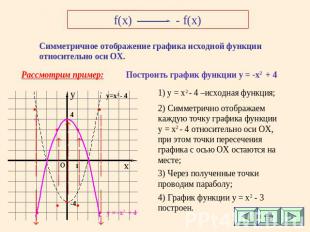
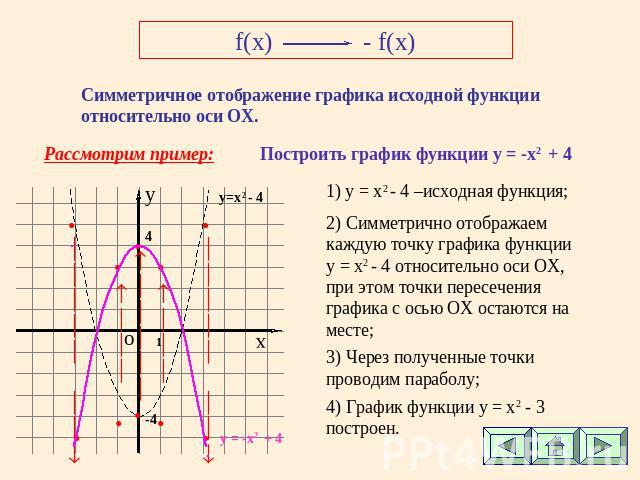
f(x)- f(x) Симметричное отображение графика исходной функции относительно оси ОХ. Рассмотрим пример: Построить график функции у = -x2 + 4 1) y = x2 - 4 –исходная функция; 2) Симметрично отображаем каждую точку графика функции у = x2 - 4 относительно оси ОХ, при этом точки пересечения графика с осью ОХ остаются на месте; 3) Через полученные точки проводим параболу; 4) График функции у = x2 - 3 построен.

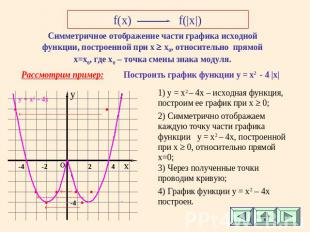
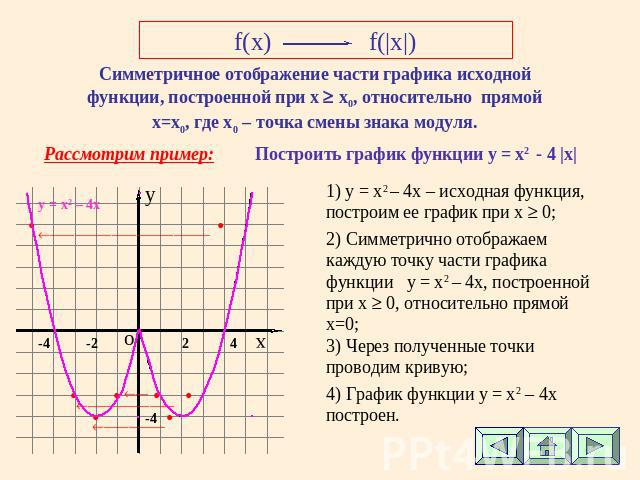
f(x) f(|x|) Симметричное отображение части графика исходной функции, построенной при х х0, относительно прямой х=х0, где х0 – точка смены знака модуля. Рассмотрим пример: Построить график функции у = x2 - 4 |х| 1) y = x2 – 4х – исходная функция, построим ее график при х 0; 2) Симметрично отображаем каждую точку части графика функции у = x2 – 4х, построенной при х 0, относительно прямой х=0; 3) Через полученные точки проводим кривую; 4) График функции у = x2 – 4х построен.

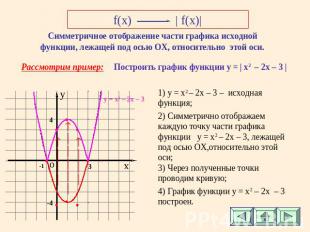
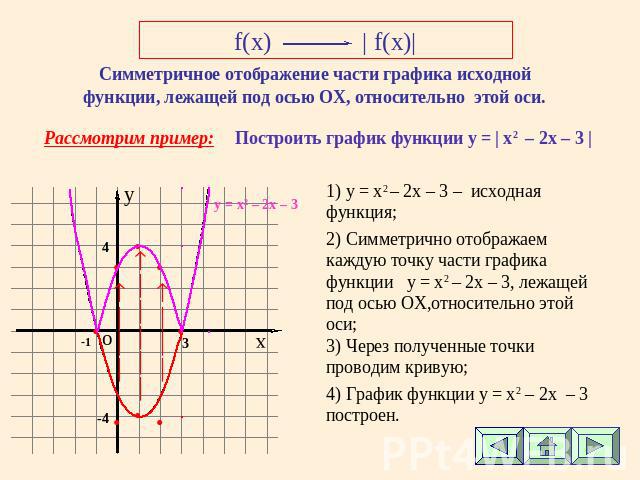
f(x)| f(x)| Симметричное отображение части графика исходной функции, лежащей под осью ОХ, относительно этой оси. 1) y = x2 – 2х – 3 – исходная функция; 2) Симметрично отображаем каждую точку части графика функции у = x2 – 2х – 3, лежащей под осью ОХ,относительно этой оси; 3) Через полученные точки проводим кривую; 4) График функции у = x2 – 2х – 3 построен.

Вам предлагается выполнить построение графиков функций с использованием движения графиков 1 уровень2 уровень3 уровень

Постройте график функции с использованием движения графиков:y =(x+2)2( f(x) f(x+a) )y = x2+1( f(x) f(x) + b )y = -x2( f(x) - f(x) )y =|x2 - 4|( f(x) f(x) + b, f(x) |f(x)| )

Постройте график функции с использованием движения графиков:y = - (x - 1)2( f(x) f(x+a), f(x) - f(x) )y = |x2 - 3| - 1( f(x) f(x) + b, f(x) - f(x), f(x) f(x) + b)y = x2 – 4х + 5

Постройте график функции с использованием движения графиков:y = | - (3 - x)2 + 1 | y = | x2 + 4|х| + 3|