Презентация на тему: Композиция функций

Композиция функций Работу выполнили ученики 10 б класса Руководитель Фомичёва Валентина Николаевна

Цели работы Разобраться, что такое композиция функций, и как применить это новое понятие на практике Потренироваться в решении заданий с функциональными уравнениями и с построениями графиков Закрепить пройденный материал по производным Заинтересовать учащихся, привлечь их внимание к данной теме

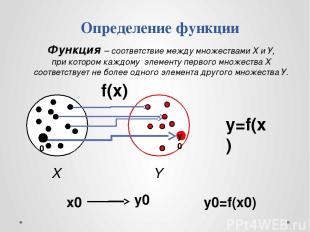
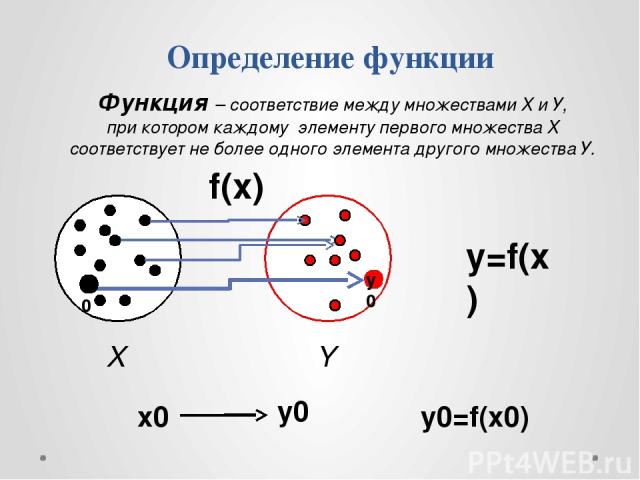
Определение функции f(x) y=f(x) Y X y0=f(x0) x0 y0 x0 у0 Функция – соответствие между множествами Х и У, при котором каждому элементу первого множества Х соответствует не более одного элемента другого множества У.

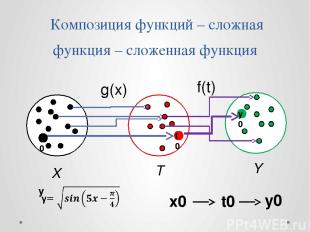
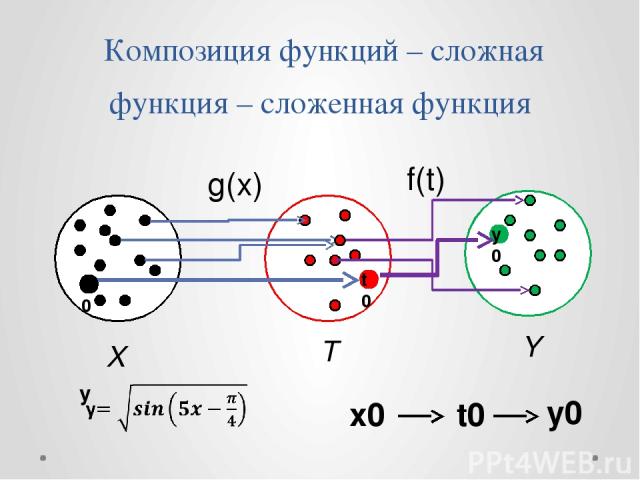
Композиция функций – сложная функция – сложенная функция g(x) f(t) T Y X x0 t0 у0 x0 t0 y0

Формула для задания сложной функции y=f(g(x)) – – сложная функция g(x) – внутренняя функция f(t) – внешняя функция Пример. g(x) = х2 - 4 – внутренняя функция f(t) = – внешняя функция

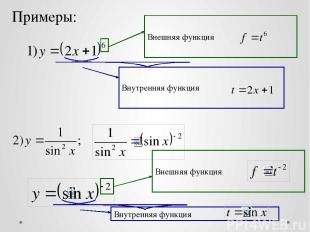
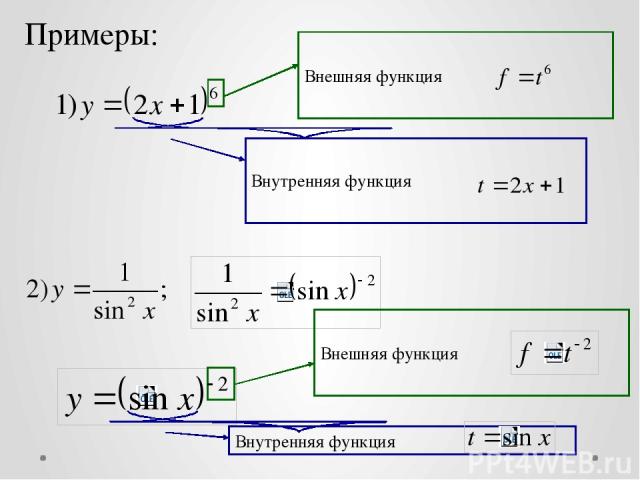
Примеры: Внешняя функция Внутренняя функция Внешняя функция Внутренняя функция

Законы композиции функций Сочетательный закон остается в силе: [(f∘g)∘h](x)=(f∘g)(h(x))= =f(g(h(x)))  , [f∘(g∘h)](x)=f[(g∘h)(x)]= =f(g(h(x)))  Распределительный закон распадается на два — из-за отсутствия перестановочного закона: f∘(g+h)=(f∘g)+(f∘h)  (g+h)∘f=(g∘f)+(h∘f)  и, что удивительно, один из них выполняется в алгебре функций, а второй — нет. Переместительный закон f∘g=g∘f  выполняется не для всех функций

Функциональные уравнения Рассмотрим задачи, в которых надо найти функцию, если задано некоторое уравнение, в котором в качестве неизвестной выступает сама функция. Пример 1 F(x) – нечетная и периодическая с периодом T = 10 Найти f(2015), если f(-5) = 1,5 Решение: Используем периодичность функции f(x). Тогда f(2015) = f(5+10*201) = f(5) Так как f(x) нечетная, то f(-x) = -f(x) => f(5) = = -f(-5)= -1,5 Ответ: -1,5

Решение функциональных уравнений методом подстановки

Примеры для самостоятельного решения

Производная композиции функций Другие производные

Правило нахождения производной композиции функций Производная сложной функции равна произведению производной внешней функции на производную внутренней функции

Применение производной композиции функций для построения графика -2 2 0 y x

Справочная литература Мордкович А.Г., Смирнова И.М. «Математика (базовый уровень)» 10 кл., 11 кл, издательство «Мнемозина». Мордкович А.Г. «Алгебра и начала математического анализа 10-11» издательство «Мнемозина» Колмогоров А.Н. и др. «Алгебра и начала математического анализа 10-11» издательство «Просвещение» Дополнительную информацию можно найти на сайтах: 1. http://www.fipi.ru 2. http://www.mathege.ru 3. http://www.reshuege.ru … 4. http://mon.gov.ru/pro/fgos http://matematikalegko.ru/proizvodnaya-pervoobraznaya/fizicheskij-smysl-proizvodnoj-zadachi-na-skorost.html  http://www.webmath.ru/primeri_reshenii/derivative.php?part=2&example=3 http://uslide.ru/algebra/12373-proizvodnaya-slozhnoy-funkcii.html http://www.webmath.ru/primeri_reshenii/derivative.php?part=2&example=5 http://www.yaklass.ru/materiali?mode=lsntheme&themeid=17 

Спасибо за внимание!