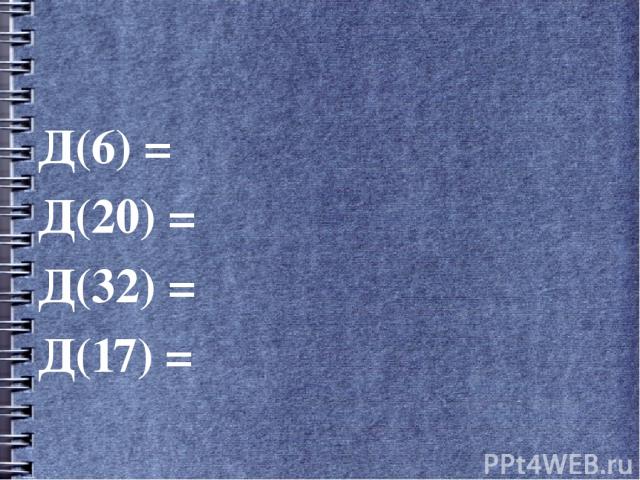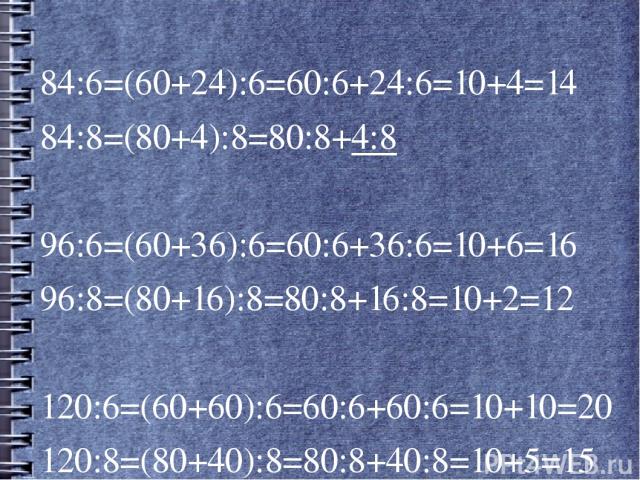Презентация на тему: Делимость произведения и суммы

МОУ Гимназия № 8 Волгограда 5 класс. Бунимович Е.А. Делимость произведения и суммы Автор: учитель математики Ковалева Елена Александровна Волгоград 2015

«Знать необходимо не затем, чтобы только знать, но и для того чтобы научиться делать.» М. Горький

Математический диктант. Какое число называют делителем натурального числа а? Какое число называют кратным  натуральному  числу а? Выпишите все делители числа 24. Напишите три числа, кратных 24. Напишите число, кратное 8 и 12.

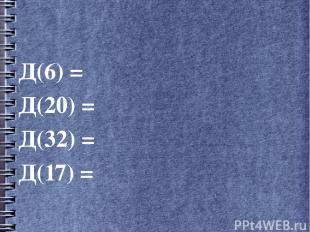
Д(6) = Д(20) = Д(32) = Д(17) =

Запишите по три числа: К(15) = К(23) = К(41) =

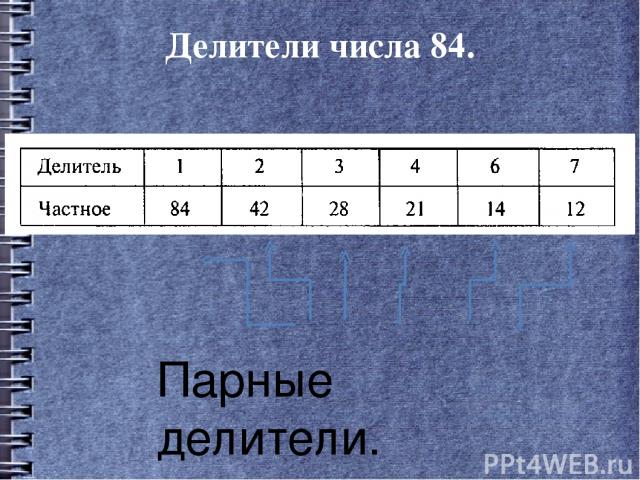
Делители числа 84.

Произведение парных делителей равно самому числу.

Запишите в порядке возрастания все делители числа 96. Д(96)=

Делимость произведения

252=12*21 а) О каких делителях числа 252 говорит это равенство? б) Укажите еще два делителя этого числа.

Не выполняя арифметических действий, докажите, что: Произведение 6*14 делится на 2? На 3? На 7? Почему? Сформулируйте правило, которое вы применили для доказательства.

1) Известно, что некоторое число делится на 10. Делится ли оно на 2? на 5? Ответ объясните. 1) Известно, что некоторое число делится на 10. Делится ли оно на 2? на 5? Ответ объясните. 2) Число а делится на 36. Укажите еще несколько делителей этого числа. Сформулируйте правило, которое вы применили для доказательства.

Не выполняя арифметических действий, докажите, что: а) произведение 12*63 делится на 42; б) степень 123 делится на 27; в) произведение 75*14 делится на 50; г) произведение 2*152 делится на 50.

Какие из чисел 84,96,120 являются общими кратными чисел 6 и 8 ?

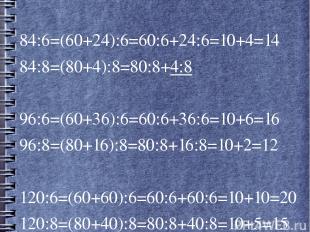
84:6=(60+24):6=60:6+24:6=10+4=14 84:8=(80+4):8=80:8+4:8 96:6=(60+36):6=60:6+36:6=10+6=16 96:8=(80+16):8=80:8+16:8=10+2=12 120:6=(60+60):6=60:6+60:6=10+10=20 120:8=(80+40):8=80:8+40:8=10+5=15

Возьмем числа 70, 49 и 14. Каждое из них делится на 7. Выясним делится ли на 7 их сумма? Возьмем числа 70, 49 и 14. Каждое из них делится на 7. Выясним делится ли на 7 их сумма? Решение: 70+ 49+ 14 = 7*10+ 7*7+ 7*2 = = 7*(10+7+2) = 7*19 Вывод:

Решаем в классе: No 356 (б)-доска и тетрадь No 357-устно No358(в,г)-доска и тетрадь No359,360(а,б)-с места

Домашнее задание: No 356(а), 358(а,б), 360(в,г) Творческое задание: Верно ли утверждение: если ни одно из слагаемых не делится на некоторое число, то и сумма не делится на это число? Подсказка: используйте контрпример.

Спасибо за урок!!!