Презентация на тему: Решение комбинаторных задач

Бесплатный обед Презентацию подготовила: Учитель математики Шестакова Ирина Александровна Муниципальное автономное общеобразовательное учреждение средняя общеобразовательная школа № 44

10 ребят решили отпраздновать день рождение в Пиццерии.

Когда все собрались ребята заспорили как им усесться вокруг стола.

Одни предлагали сесть по алфавитному порядку, другие по возрасту, третьи по успеваемости, четвертые по росту и т. д. Спор затянулся, пицца остыла, за стол никто не садился.

Примерил всех официант. Он сказал: - Молодые мои друзья оставьте свои пререкания. Сядьте за стол как кому приедется и выслушайте меня. Все сели как попало.

- Пусть один из вас сейчас запишет,в каком порядке вы сейчас сидите. Завтра вы снова явитесь сюда пообедать и разместитесь уже в ином порядке. Послезавтра сядете опять по-новому и т. д. Когда же придет черед сесть также как вы сидите сейчас, тогда – я торжественно обещаю- угощать вас бесплатно пиццей. Предложение всем понравилось. Решено было каждый день собираться в этой пиццерии и перепробовать все способы размещения за столом, чтобы скорее начать пользоваться бесплатными обедами.

Ребята, вы бы согласились на условие официанта? Выполнил ли официант обещанное?

Официант не исполнил свое обещание, так как число всех возможных размещений за столом чересчур велико! Оно равняется 3 628 800. Такое число размещений составляет почти 10 000 лет.

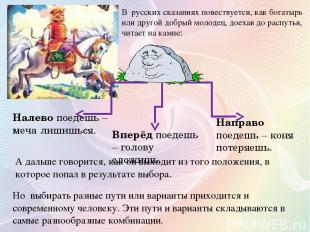
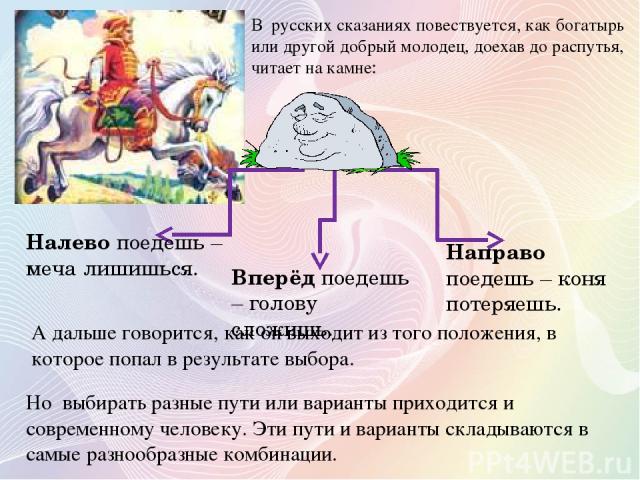
В русских сказаниях повествуется, как богатырь или другой добрый молодец, доехав до распутья, читает на камне: Вперёд поедешь – голову сложишь. Направо поедешь – коня потеряешь. Налево поедешь – меча лишишься. А дальше говорится, как он выходит из того положения, в которое попал в результате выбора. Но выбирать разные пути или варианты приходится и современному человеку. Эти пути и варианты складываются в самые разнообразные комбинации.

Рассмотренная задача относиться к области математики, называемой комбинаторикой. При решении комбинаторных задач чаще всего приходится отвечать на вопрос: «Сколькими способами…?» Ребята сформулируйте тему урока. Тема урока: Решение комбинаторных задач.

Люди, которые умело владеют техникой решения комбинаторных задач, а следовательно, обладают хорошей логикой, умением рассуждать, перебирать различные варианты решений, очень часто находят выходы, казалось бы, из самых трудных безвыходных ситуаций. Мы будем относиться к их числу? Тогда, на уроке работайте старательно И успех вас ждёт обязательно!

Работа с текстом учебника. Стр.42 . Составить вопросы по тексту.

Способ перебора всех воможных вариантов. №137

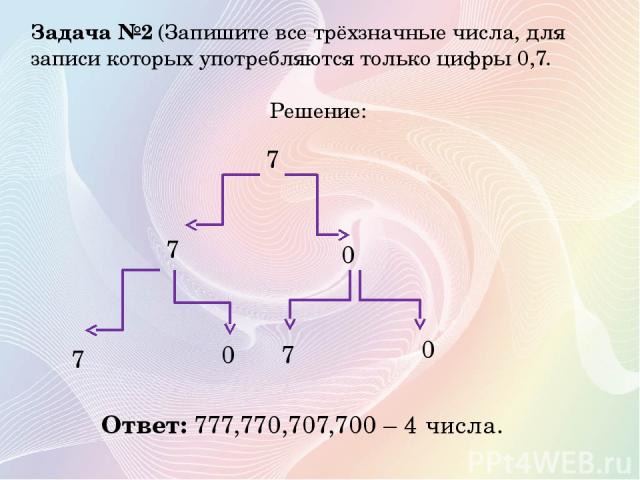
Задача №2 (Запишите все трёхзначные числа, для записи которых употребляются только цифры 0,7. Решение: 7 7 0 7 7 0 0 Ответ: 777,770,707,700 – 4 числа.

Данная схема называется деревом возможных вариантов. Ребята,как вы думаете почему? В каких случаях удобней применять этот способ?

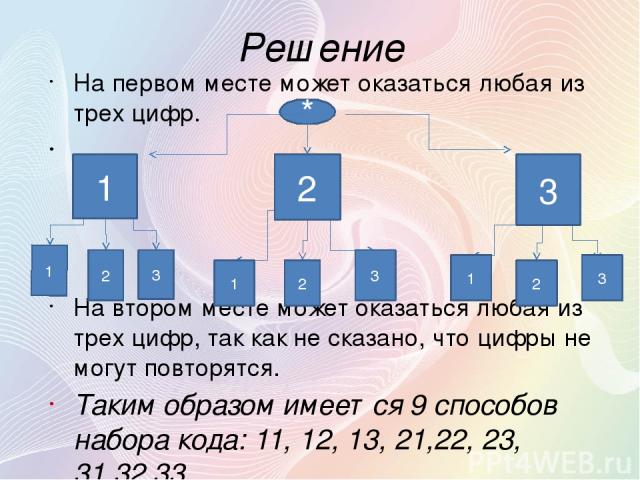
Задача Чтобы запереть чемодан с кодовым замком, состоящий из двух каких либо цифр. Хозяин решил использовать только цифры 1, 2 и 3. Сколькими способами он может выбрать код?

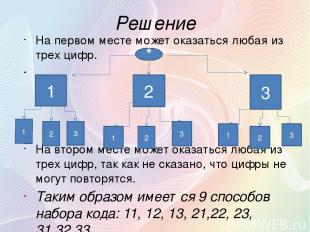
Решение На первом месте может оказаться любая из трех цифр. На втором месте может оказаться любая из трех цифр, так как не сказано, что цифры не могут повторятся. Таким образом имеется 9 способов набора кода: 11, 12, 13, 21,22, 23, 31,32,33. 1 2 3 1 2 3 1 2 3 1 2 3 *

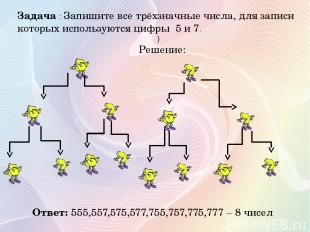
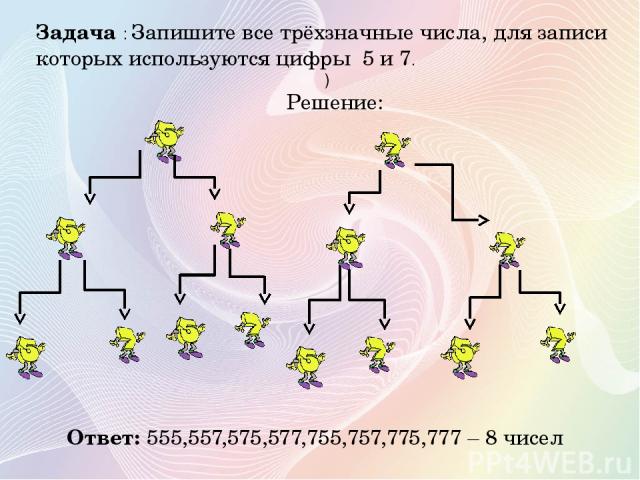
Задача : Запишите все трёхзначные числа, для записи которых используются цифры 5 и 7. ) Решение: Ответ: 555,557,575,577,755,757,775,777 – 8 чисел

Домашнее задание П.2.5 читать составить вопросы № 138, 143

Подведем итог: О чем мы сегодня говорили на уроке? Что нового для себя узнали? Что интересного для себя узнали на уроке?