Презентация на тему: Решение комбинаторных задач

Решение комбинаторных задач

* * Термин «комбинаторика» был введён в математический обиход немецким философом, математиком Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве». Термин «комбинаторика» происходит от латинского слова «combinare», что в переводе на русский означает – «сочетать», «соединять». Комбинаторика - это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.

* Из истории комбинаторики С комбинаторными задачами люди столкнулись и в глубокой древности. В Древнем Китае увлекались составлением магических квадратов. В Древней Греции занимались теорией фигурных чисел. Комбинаторные задачи возникли и в связи с такими играми, как шашки, шахматы, домино, карты, кости и т.д. Комбинаторика становится наукой лишь в 18 в. – в период, когда возникла теория вероятности.

Тео рия вероя тностей — это раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.

* Выбором объектов и расположением их в том или ином порядке приходится заниматься чуть ли не во всех областях человеческой деятельности, например конструктору, разрабатывающему новую модель механизма, ученому-агроному, планирующему распределение с/х культур на нескольких полях, химику, изучающему строение органических молекул, имеющих данный атомный состав.

Что значит решить комбинаторную задачу? Решить комбинаторную задачу - это значит выписать или сосчитать все возможные комбинации (способы, варианты) составленные из объектов (цифр, букв, чисел, слов, предметов и др.,) отвечающих условию задачи.

На завтрак в школьной столовой можно выбрать кашу манную, гречневую, овсяную или рисовую, запить можно чаем с лимоном, какао или соком морковным. Сколько вариантов завтрака есть?

Выбор напитка – выбор объекта А Выбор каши - выбор объекта В Объект А имеет 3 варианта выбора, а объект В - 4, вариантов выбора пары объектов А и В 3•4=12.

ПРАВИЛО УМНОЖЕНИЯ Если объект А можно выбрать m способами и если после каждого такого выбора объект В можно выбрать n способами, то выбор пары (А и В) ,в указанном порядке, можно осуществить m●n способами. При этом число способов выбора второго объекта не зависит от того, как именно выбран первый объект.

Игра в кости

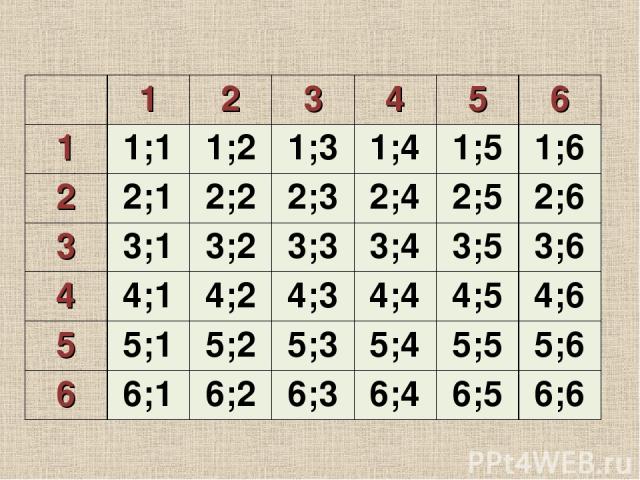
Решите задачу Сколько может быть различных комбинаций выпавших граней при бросании двух игральных костей? Решение: На первой кости может быть: 1,2,3,4,5 и 6 очков, т.е. 6 вариантов. На второй – 6 вариантов. Всего: 6*6=36 вариантов. Ответ: всего 36 комбинаций

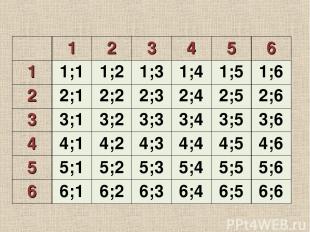
1 2 3 4 5 6 1 1;1 1;2 1;3 1;4 1;5 1;6 2 2;1 2;2 2;3 2;4 2;5 2;6 3 3;1 3;2 3;3 3;4 3;5 3;6 4 4;1 4;2 4;3 4;4 4;5 4;6 5 5;1 5;2 5;3 5;4 5;5 5;6 6 6;1 6;2 6;3 6;4 6;5 6;6

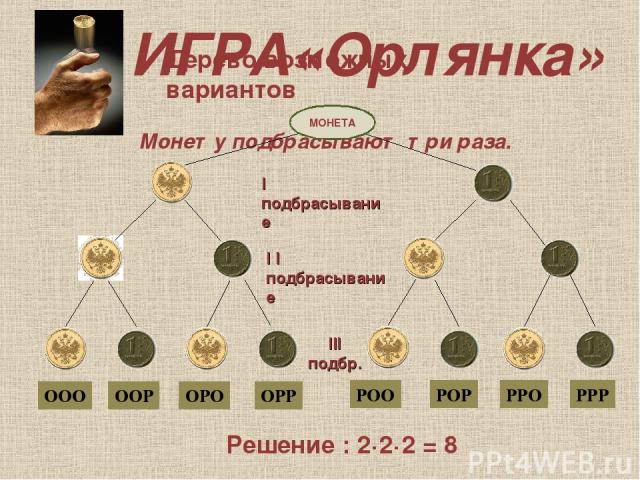
ИГРА«Орлянка» Монету подбрасывают три раза. ООО ООР ОРО ОРР РОО РОР РРО РРР МОНЕТА Решение : 2·2·2 = 8 I подбрасывание I I подбрасывание III подбр. Дерево возможных вариантов

Мы шагаем, мы шагаем. Руки выше поднимаем, Голову не отпускаем, Дышим ровно, глубоко. Вдруг мы видим у куста Выпал птенчик из гнезда. Тихо птенчика берем И назад в дупло кладем. Впереди из-за куста Смотрит хитрая лиса. Мы лисицу обхитрим, На носочках побежим. На полянку мы заходим, Много ягод там находим. Одну ягодку беру, На другую смотрю, Третью примечаю Нам радостно, нам весело! Смеемся мы ХА - ХА. Но вот пришло мгновенье, Серьезным быть пора. Глазки прикрыли, ручки сложили, Головки опустили, ротик закрыли. И затихли на минутку, Чтоб не слышать даже шутку, Чтоб не видеть никого, А себя лишь одного! Физкультминутка

Комбинаторные задачи на умножение. Имеется 3 вида конвертов и 4 вида марок. Сколько существует вариантов выбора конверта с маркой? В кружке 6 учеников. Сколькими способами можно выбрать старосту кружка и его заместителя? В буфете есть 4 сорта пирожков (не меньше двух штук каждого сорта). Сколькими способами ученик может купить себе 2 пирожка? Сколько все трехзначных числел, в записи которых используются цифры 0,1,2 при условии, что: 1)Все цифры в числах разные 2)Цифры в числах могут повторяться Решение: 6 · 5 = 30 Решение: 3 · 4 = 12 Решение: 2 · 3 · 3 = 18 Решение: 4 · 4 = 16 Решение: 2 · 2 · 1 = 4

Самостоятельная работа * Вариант 1 Вариант 2 1.Сколько существует способов рассадить 5 человек за столом? 1.Сколько существует способов расставить 4 книги на полке? 2. Сколькими способами можно составить флаг, состоящий из трех горизонтальных полос различных цветов, если имеется материал пяти цветов? 3.Сколько четных двузначных чисел можно составить из цифр 0,1,2,4,5,9? 2.Сколько комплектов одежды (блузка+юбка) можно составить из двух блузок и пяти юбок? 3.Сколько трёхзначных чисел кратных 10 можно составить из цифр 0,3,5,7,9?

Задача.При встрече каждый из друзей пожал другому руку (каждый пожал каждому). Сколько рукопожатий было сделано, если друзей было: 1)трое 2)четверо 3)пятеро Подсчет вариантов с помощью графов Решать некоторые математические задачи помогают специальные схемы, состоящие из точек и соединяющих их дуг или стрелок. Такие схемы называют графами, точки называют вершинами графа, а дуги – рёбрами графа.