Презентация на тему: Решение комбинаторных задач с помощью бинома Ньютона и полиномиальной формулы

Научно - практическая конференция школьников "Эврика"Решение комбинаторных задачс помощью бинома Ньютона и полиномиальной формулыНаучно – исследовательский проектВыполнен ученицей 10 «А» классаСОШ № 74 г. КраснодараЩегольковой АннойНаучный руководитель – учитель математики СОШ № 74Забашта Елена Георгиевна

Цель:изучить и применить бином Ньютона и полиномиальную формулу к решению некоторых комбинаторных задач Задачи:1) ознакомиться с формулой бинома Ньютона и ее свойствами, рассмотреть треугольник Паскаля и метод его построения;2) ознакомиться с полиномиальной формулой как обобщением бинома Ньютона;3) рассмотреть некоторые комбинаторные задачи, решаемые с помощью бинома Ньютона и полиномиальной формулы.

Язык перечислительнойкомбинаторики

Бином Ньютонаи его свойства1.Число всех членов разложения на единицу больше показателя степени бинома, т.е. равно n + 1.2. Сумма показателей степени a и b каждого члена разложения равна показателю степени бинома.3. Общий член разложения имеет вид 4. Коэффициенты разложения, одинаково удаленные от концов разложения, равны между собой . Правило симметрии 5. Правило Паскаля

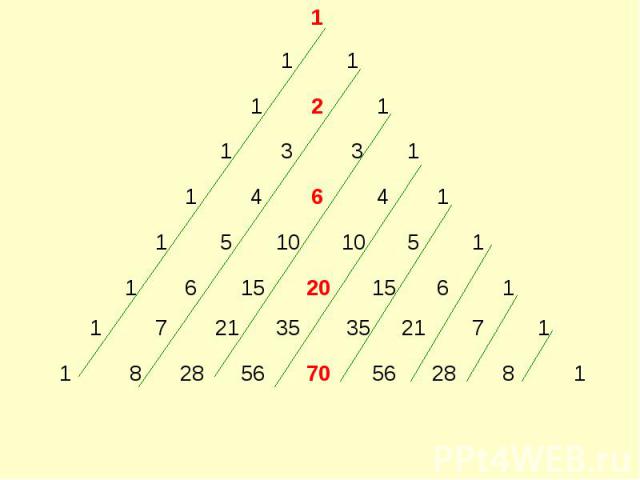
Треугольник Паскаля

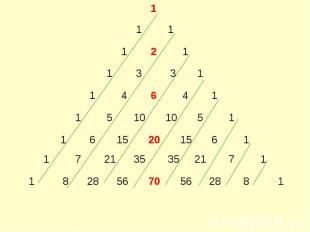
Некоторые соотношения для биномиальных коэффициентовПолиномиальная формула

Задача № 1Доказать, что делится нацело на 64 при любом натуральном n. Доказательство.Обозначив выражение в скобках через а, а N, имеем:Полученная сумма делится на 64, что и требовалось доказать.

Задача № 2 Доказать неравенство Бернуллиc > 1 + n (c – 1), где с – произвольное число, большее 1, n – натуральное число, большее 1. Доказательство.Для каждого натурального n и чисел a = 1 и b = c-1 верны равенстваПо условию b > 0 и n > 2. Следовательно, каждое слагаемое (их по меньшей мере три) в полученной сумме строго положительно. Значит, и доказываемое неравенство верно.

Задача № 3Найти разложение степени бинома Решение.Задача № 4Найти разложение степени тринома