Презентация на тему: Функции нескольких переменных

Математический анализ Составитель: Никулина Л.С., старший преподаватель кафедры Математики и Моделирования

Литература Основная литература: Л. Д. Кудрявцев. Курс математического анализа, т. 1, 2 Г. Н. Берман. Сборник задач по курсу математического анализа. Н. С. Пискунов. Дифференциальное и интегральное исчисления, т. 1, 2.

Дополнительная литература: Кудрявцев В. А., Демидович Б. П. Краткий курс высшей математики Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах, ч. 1, 2.

Учебно-методические разработки: Л. Я. Дубинина, Л. С. Никулина, И. В. Пивоварова. Курс лекций по высшей математике, ч. 1, 2.-Владивосток, изд. ВГУЭиС, 2001. Сборник задач по высшей математике. Сост. И. В. Пивоварова, Л. Я. Дубинина, Л. С. Никулина. -Владивосток, изд. ВГУЭиС, 2002.

Содержание Функции нескольких переменныхДифференциальные уравнения 1-го, 2-го и более высокого порядковКратные интегралыЧисловые рядыСтепенные рядыРяды Фурье

Функции нескольких переменных Лекция 1

Определение функции двух переменных Определение. Если каждой паре (x,y) значений двух независимых друг от друга переменных величин x и y из некоторого множества D соответствует единственное значение величины z, а каждому z соответствует хотя бы одна пара (x,y), то мы говорим, что z есть функция двух независимых переменных x и y, определенная в D.

Обозначения При этом пишут: Если паре соответствует число , то пишут Или называется частным значением функции при

График функции 2-х переменных Геометрическое место точек, координаты которых удовлетворяют уравнению z= =f(x,y), называется графиком функции двух переменных.

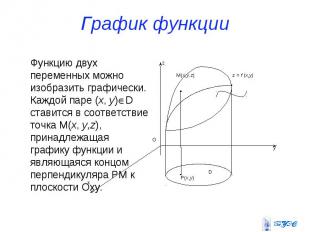
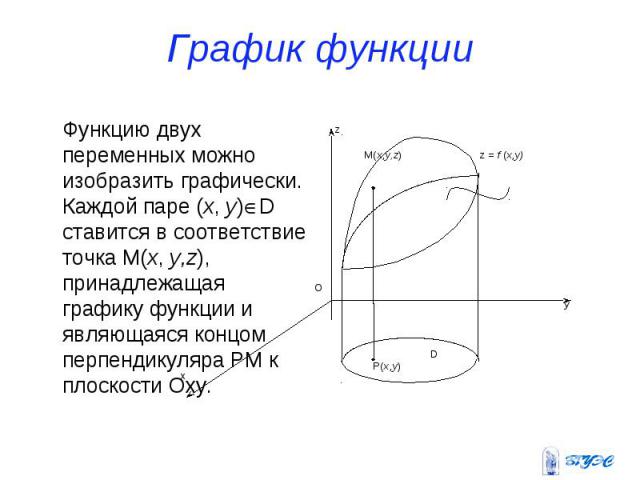
График функции Функцию двух переменных можно изобразить графически. Каждой паре (x, y)D ставится в соответствие точка M(x, y,z), принадлежащая графику функции и являющаяся концом перпендикуляра PM к плоскости Oxy.

Предел функции 2-х переменных Окрестностью радиуса R точки называется совокупность всех точек, лежащих внутри круга радиуса R с центром в точке , кроме самой точки.

Предел функции 2-х переменных Таким образом, окрестностью точки является множество точек, УДОВЛЕТВОРЯЮЩИХ НЕРАВЕНСТВУ

Определение предела функции 2-х переменных Число А называется пределом функции z=f(x,y) при , если для любого числа найдется такое число R>0, что для всех точек М(х,у), лежащих в окрестности радиуса R точки , выполняется условие При этом пишут: или

Непрерывность Функция z=f(x,y) называется непрерывной в точке , если выполнены условия: 1)функция определена в точке , 2)если существует ,3)если

Непрерывность Другое определение: Функция z=f(x,y) называется непрерывной в точке , если в этой точке бесконечно малому приращению аргументов соответствует бесконечно малое приращение функции, т. е. где .

Внутренние и граничные точки Линию, ограничивающую некоторую область D в плоскости Oxy, мы будем называть границей этой области. Точки области, не лежащие на границе области, мы будем называть внутренними точками области, если они принадлежат области вместе со своей окрестностью.

Открытая и замкнутая области Область, состоящую из одних внутренних точек, мы будем называть открытой или незамкнутой. Если же к области относятся еще и точки границы, то область называют замкнутой.

Ограниченная область Область называют ограниченной, если существует такое постоянное C>0, что расстояние любой точки M области от начала координат O меньше C, т.е. .

Наибольшее и наименьшее значения функции Теорема Вейерштрасса. Непрерывная функция в замкнутой ограниченной области D достигает по крайней мере один раз наибольшего значения M и наименьшего значения m.

Частные приращения функции 2-х переменных Разность = f (x+x, y) – f (x, y) называется частным приращением функции f (x, y) по переменной x. Разность = f (x, y+y) – f (x, y) называется частным приращением функции f (x, y) по переменной y.

Частные производные Определение. Если существует = , то он называется частной производной (первого порядка) функции z = f (x, y) по переменной x и обозначается

Продолжение Аналогично определяется частная производная по переменной y: = Эту производную обозначают

Производные высших порядков Частной производной n-го порядка функции нескольких переменных называется частная производная первого порядка от частной производной (n-1)-го порядка той же функции. Например, для функции 2-х переменных имеем:

Равенство смешанных производных Теорема. Две смешанные частные производные одной и той же функции, отличающиеся лишь порядком дифференцирования, равны между собой при условии их непрерывности. Так, ,