Презентация на тему: Дифференциал функции нескольких переменных

Полный дифференциал функции нескольких переменных Лекция 2 900igr.net

Полное приращение функции 2-х переменных Если обеим переменным дать приращение, то функция получит полное приращение

Определение дифференцируемой функции Функция называется дифференцируемой в точке М(х,у), если ее полное приращение можно представить в виде , где Δx и Δy -произвольные приращения аргументов х и у в некоторой окрестности точки М(х,у), А и В –постоянные, независящие от Δx и Δy , o(ρ)-бесконечно малая более высокого порядка, чем -расстояние между М(х,у) и

Определение дифференциала Главная линейная относительно Δx и Δy часть полного приращения функции называется полным дифференциалом этой функции и обозначается dz или df(x,y) . Таким образом, .

Формула для вычисления дифференциала Если функция дифференцируема в точке М(х,у),то она имеет в этой точке частные производные и , причем =А, а =В . Таким образом, . Если положить ,то

Дифференциалы высшего порядка Дифференциалом второго порядка функции z=f(x,y) называется Вообще: Если х и у независимые переменные, то .

Достаточные условия дифференцируемости функции Пусть функция в некоторой окрестности точки М(х,у)имеет частные производные , и ,которые непрерывны в самой точке М. Тогда функция дифференцируема в этой точке.

Достаточные условия дифференцируемости функции Опр. Функция, имеющая в некоторой точке непрерывные частные производные, называется непрерывно дифференцируемой в этой точке.

Экстремумы функции двух переменных Определение. Говорят, что в точке функция f (x,y) имеет максимум, если cуществует такая окрестность этой точки, что для всех точек P(x,y) этой окрестности, отличных от , выполнено неравенство Аналогично определяется минимум функции. Минимум и максимум функции называются ее экстремумами. .

Экстремумы функции двух переменных Теорема (необходимое условие экстремума). В точке экстремума функции нескольких переменных каждая ее частная производная либо равна нулю, либо не существует. Точки, в которых выполнены эти условия, называются критическими.

Достаточные условия экстремума функции двух переменных Теорема. Пусть функция z=f(x,y) определена и имеет непрерывные частные производные второго порядка в некоторой окрестности точки , в которой . Если при этом в этой точке выполнено условие , то точка является точкой экстремума функции, причем точкой максимума, если , и точкой минимума, если . Если же в этой точке , то экстремума в точке нет. В том случае, если в точке , теорема ответа не дает.

Наибольшее и наименьшее значения функции Определение. Наименьшее или наибольшее значение функции в данной области называется абсолютным экстремумом функции (абсолютным минимумом или абсолютным максимумом соответственно) в этой области.

Согласно теореме Вейерштрасса непрерывная в замкнутой ограниченной области функция достигает в ней своих наибольшего и наименьшего значений. Абсолютный экстремум достигается функцией либо в критических точках, либо на границе области.

Скалярное поле Лекция 3

Основные определения Пусть в области D пространства Охуz задана функция u=u(х,у,z). В этом случае говорят, что в области D задано скалярное поле, а саму функцию u=u(х,у,z)называют функцией поля. Например, поле давлений, температур и т.д.

Основные определения Множество точек М области D, для которых скалярное поле сохраняет постоянное значение, т. е. u(М)=С, называется поверхностью уровня ( или изоповерхностью) скалярного поля. Если область D расположена на плоскости Оху, то поле u=u(х,у) является плоским. Поверхности уровня называют в этом случае линиями уровня.

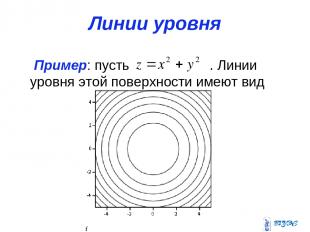
Линии уровня Пример: пусть . Линии уровня этой поверхности имеют вид

Производная по направлению Пусть задана дифференцируемая функция скалярного поля u=u(x,y,z) . Производной этой функции по направлению l называется

Вычисление производной по направлению Производную по направлению вычисляют по формуле где cosα, cosβ , cosγ-направляющие косинусы вектора . Для плоского скалярного поля

Градиент скалярного поля Градиентом скалярного поля u=u(x,y,z), где u=u(x,y,z)-дифференцируемая функция, называется вектор с координатами . Таким образом, или .

Пример Найти градиент функции u= в точке M(6,2,3). Решение. Вычислим градиент функции. Тогда grad u = + +

Направление градиента Теорема. Производная функции по направлению равна проекции градиента этой функции на данное направление (в соответствующей точке).

Направление градиента Так как производная по направлению представляет собой скорость изменения функции в данном направлении , а проекция вектора на другой вектор имеет максимальное значение, если оба вектора совпадают по направлению, то градиент функции в данной точке указывает направление наиболее быстрого возрастания функции. .

Величина градиента плоского скалярного поля Величина градиента плоского скалярного поля ,т.е. grad u = обозначается tg и определяет крутизну наибольшего ската или подъема поверхности u = f (x, y).

Продолжение Градиент скалярного поля в данной точке по величине и направлению равен максимальной скорости изменения поля в этой точке, т. е. , где .

Направление градиента Точка Р, в которой gradu(P)=0, называется особой точкой скалярного поля. В противном случае эту точку называют неособой или обыкновенной точкой поля. Теорема. Во всякой неособой точке плоского скалярного поля градиент поля направлен по нормали к линии уровня , проходящей через эту точку, в сторону возрастания поля.