Презентация на тему: Графическое решение квадратных уравнений

* Урок алгебры в 8 классе по учебно-методическому пособию А.Г.Мордкович Автор презентации : учитель математики МОУ «СОШ п.Целинный Перелюбского района Саратовской области» Тасмухамбетова Н.Н 5klass.net

* Графическое решение квадратных уравнений

* Квадратным уравнением называется уравнение вида где а, в ,с – заданные числа, причем а ≠ 0

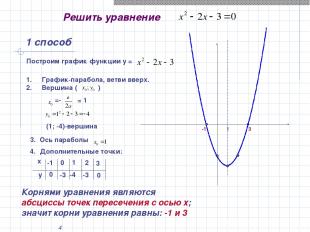
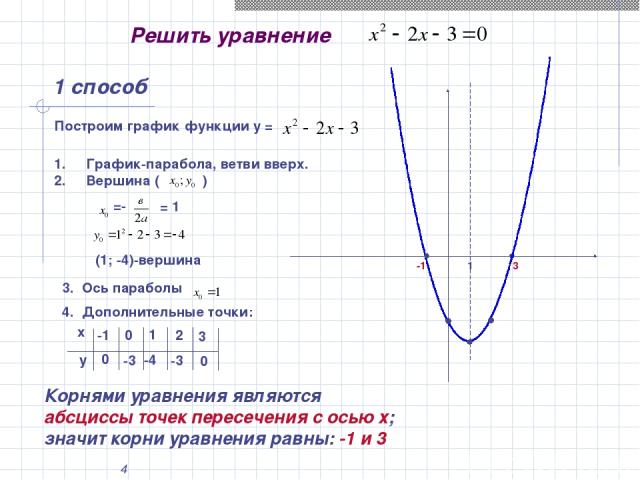
* Решить уравнение 1 способ Корнями уравнения являются абсциссы точек пересечения с осью х; значит корни уравнения равны: -1 и 3 -1 3 1

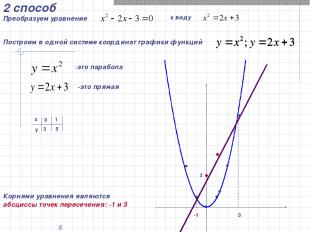
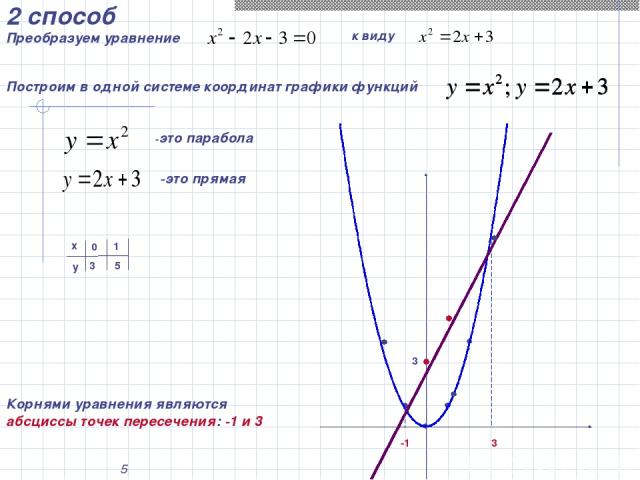
* 2 способ Преобразуем уравнение к виду Построим в одной системе координат графики функций -это парабола -это прямая х у 0 1 3 5 3 -1 3 Корнями уравнения являются абсциссы точек пересечения: -1 и 3

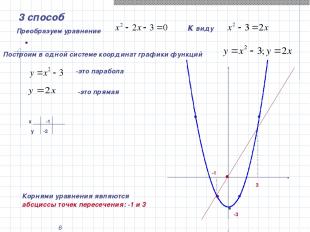
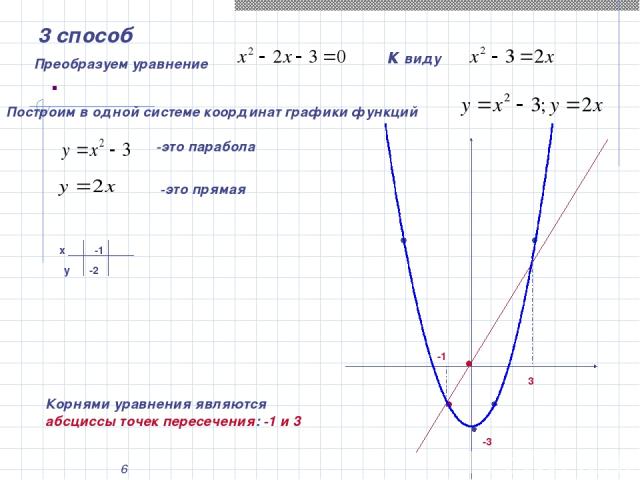
* . 3 способ Преобразуем уравнение к виду Построим в одной системе координат графики функций -это парабола -это прямая х у -1 -2 -1 3 Корнями уравнения являются абсциссы точек пересечения: -1 и 3 -3

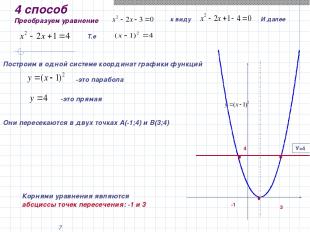
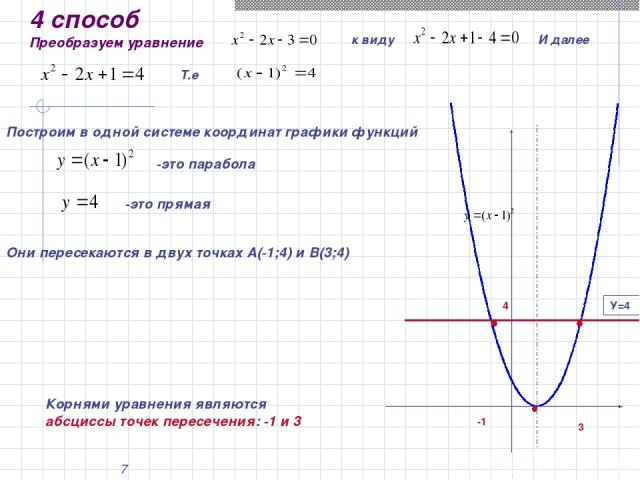
* 4 способ Преобразуем уравнение к виду Построим в одной системе координат графики функций И далее Т.е -это парабола -это прямая Они пересекаются в двух точках А(-1;4) и В(3;4) -1 4 У=4 3 Корнями уравнения являются абсциссы точек пересечения: -1 и 3

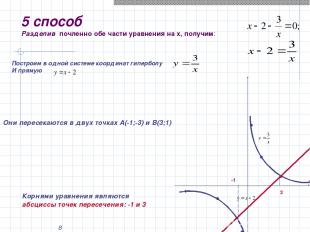
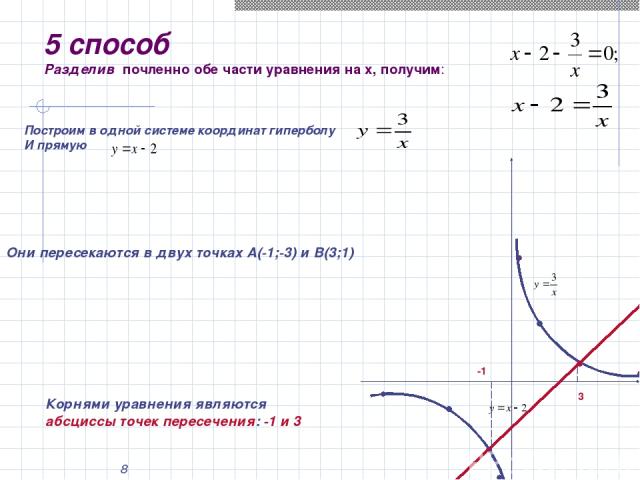
* 5 способ Разделив почленно обе части уравнения на х, получим: Построим в одной системе координат гиперболу И прямую Они пересекаются в двух точках А(-1;-3) и В(3;1) -1 3 Корнями уравнения являются абсциссы точек пересечения: -1 и 3

* Заметим , что первые четыре способа применимы к любым уравнениям вида ,а пятый – только к тем, у которых с =0

* Историческая справка Первые упоминания о способах решения уравнений, которые мы сейчас называем квадратными относятся ко второму тысячелетию до н.э. Это эпоха расцвета Вавилонии и Древнего Египта. Первое тысячелетие н.э. – Римские завоевательные войны. К этому периоду относится творчество Диофанта. Его трактат “Арифметика” содержит ряд задач, решаемых при помощи квадратных уравнений. В IX веке узбекский математик Аль-Хорезми в Трактате “Алгебра” классифицирует квадратные уравнения. Для нас это время знаковое тем, что приблизительно в это время образуется древнерусское государство Киевская Русь. Все это время отличные по записи уравнения считались различными. Не было единого подхода к их решению. И только в XVI веке французский юрист, тайный советник короля Франции и математик Франсуа Виет впервые вводит в обращение буквенные обозначения не только для неизвестных величин, но и для данных, то есть коэффициентов уравнения. Тем самым он заложил основы буквенной алгебры.

*

*

* (Я. А. Коменский) “Учиться нелегко, но интересно”.