Презентация на тему: Графики

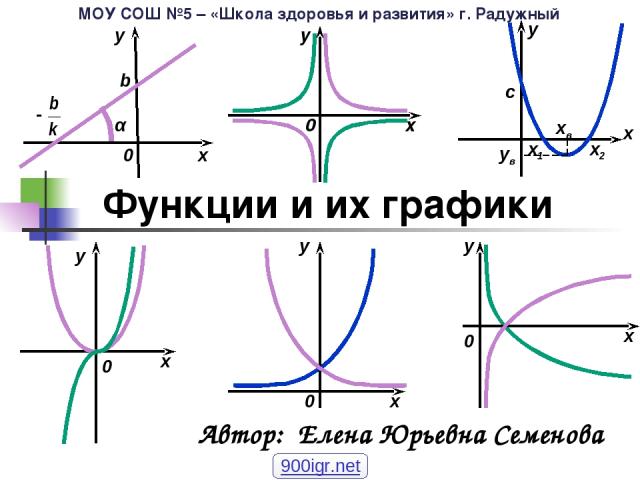
Функции и их графики Автор: Елена Юрьевна Семенова МОУ СОШ №5 – «Школа здоровья и развития» г. Радужный 900igr.net

Содержание Функции и их графики. Преобразование графиков функций. Свойства функций.

Функции. Линейная функция Квадратичная функция Степенная функция Обратная пропорциональность Показательная функция Логарифмическая функция Тригонометрические функции

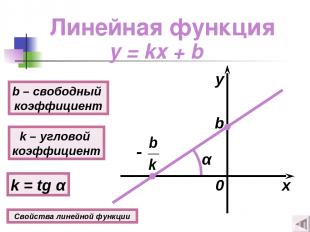
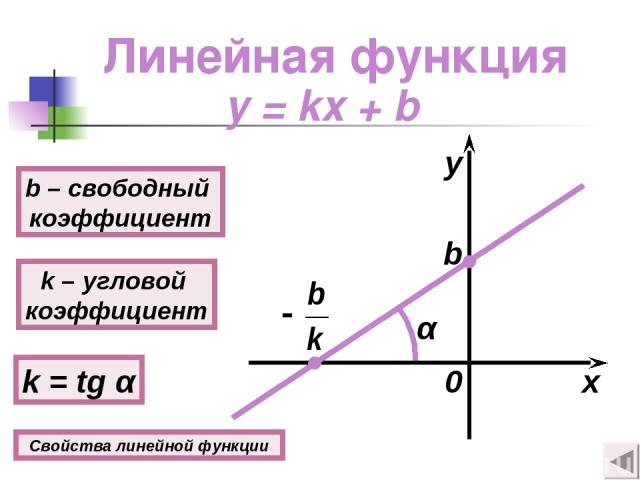
Линейная функция y = kx + b k – угловой коэффициент k = tg α b – свободный коэффициент b x y α 0 Свойства линейной функции

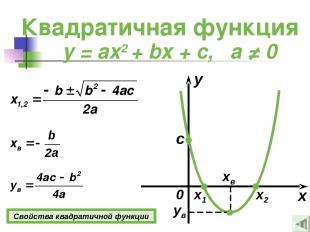
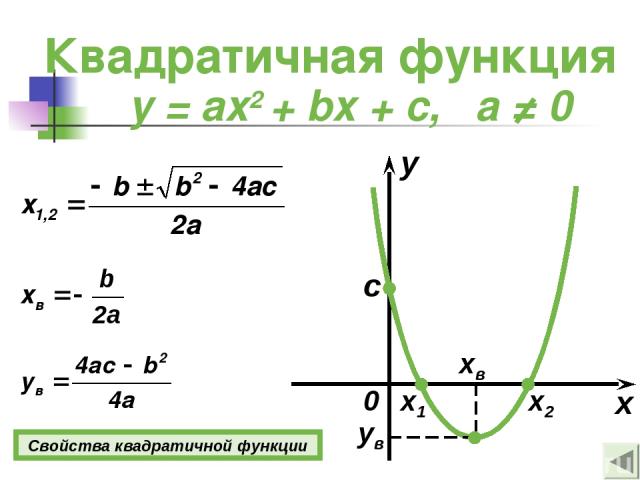
Квадратичная функция y = ax2 + bx + c, а ≠ 0 x y 0 c x1 x2 xв ув Свойства квадратичной функции

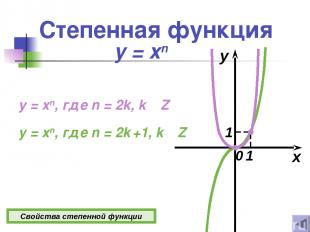
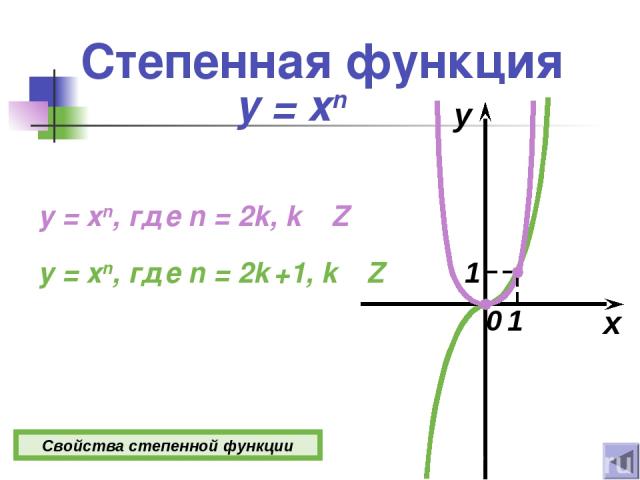
Степенная функция y = xn x y 0 y = xn, где n = 2k, k Z y = xn, где n = 2k +1, k Z Свойства степенной функции 1 1

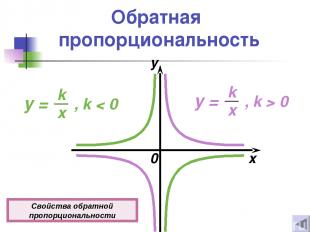
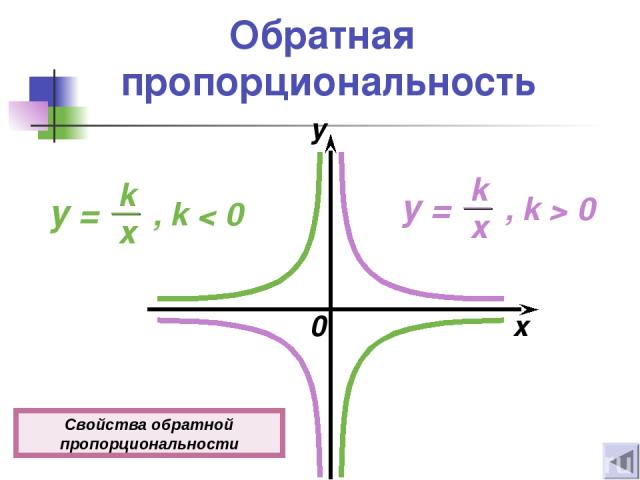
Обратная пропорциональность 0 x y Свойства обратной пропорциональности

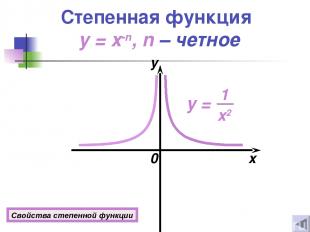
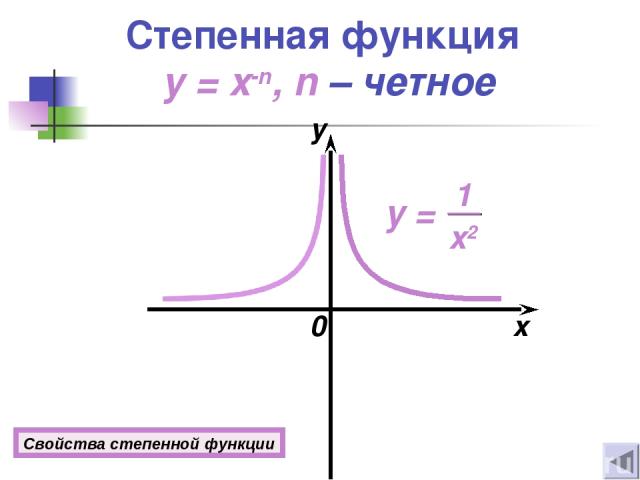
Степенная функция y = x-n, n – четное 0 x y Свойства степенной функции

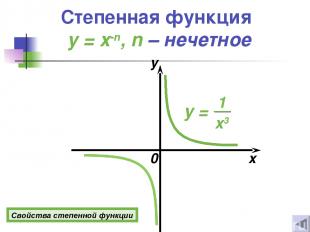
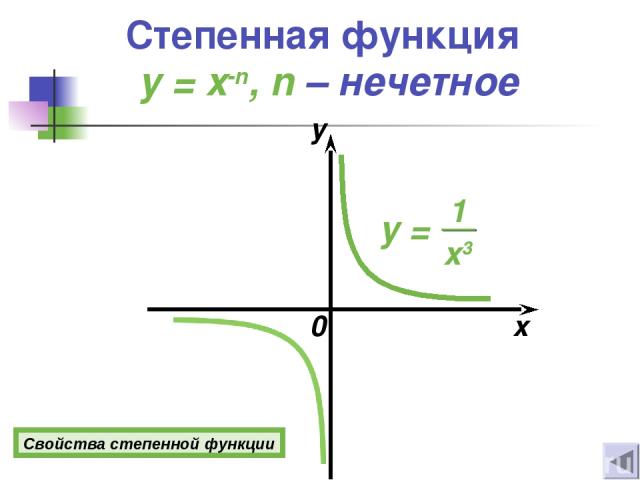
0 x y Свойства степенной функции Степенная функция y = x-n, n – нечетное

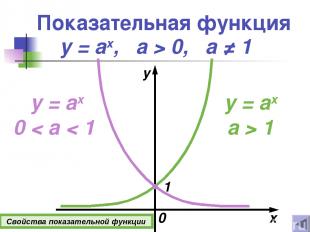
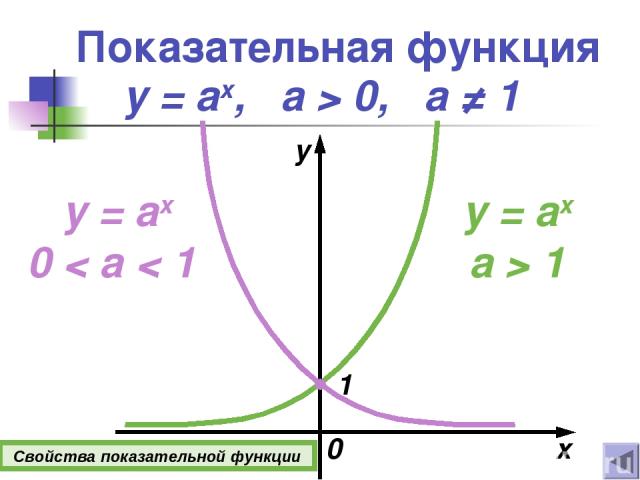
Показательная функция x y y = ax, а > 0, a ≠ 1 y = ax a > 1 y = ax 0 < a < 1 1 0 Свойства показательной функции

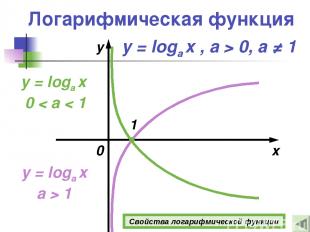
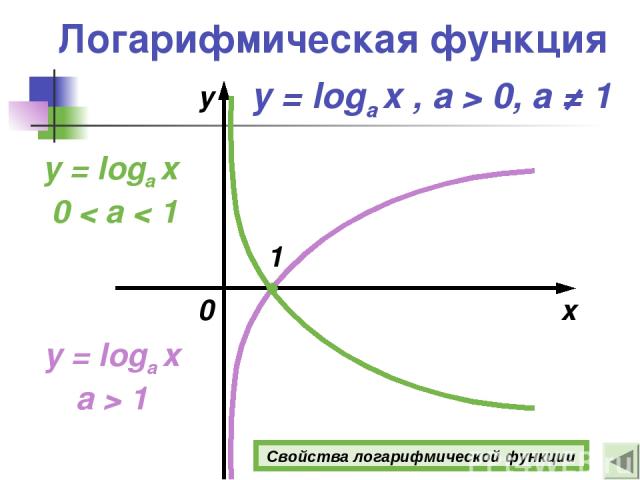
Логарифмическая функция y = loga x a > 1 x y y = loga x 0 < a < 1 1 0 y = loga x , а > 0, a ≠ 1 Свойства логарифмической функции

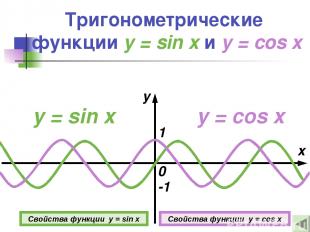
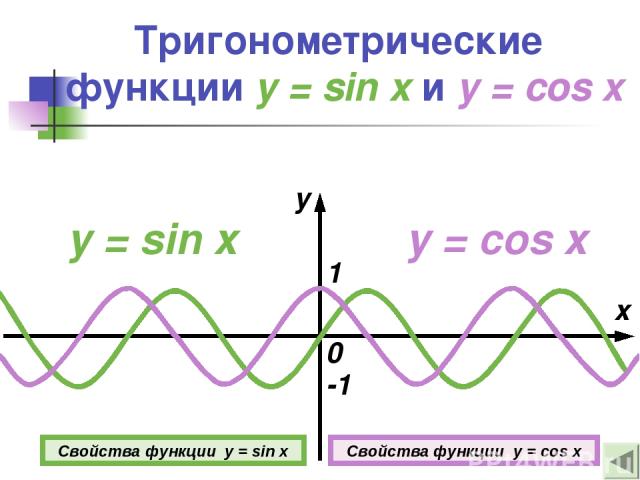
Тригонометрические функции y = sin x и y = cos x y = sin x x y 0 1 -1 y = cos x Свойства функции y = sin x Свойства функции y = cos x

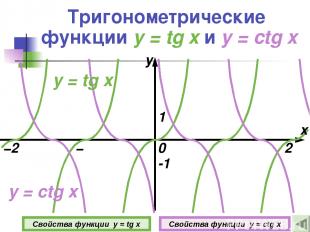
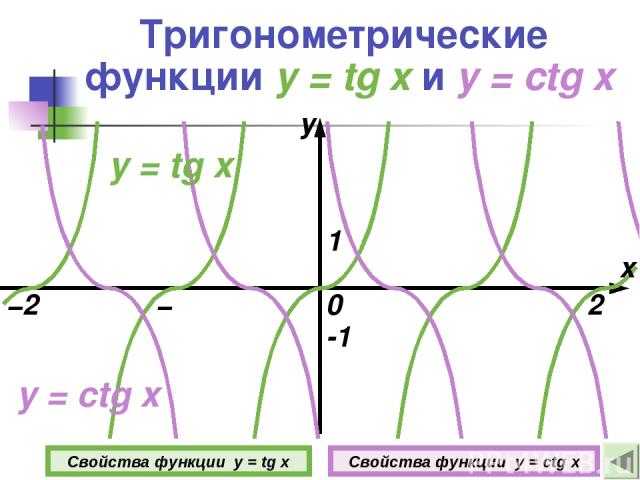
Тригонометрические функции y = tg x и y = ctg x 0 1 -1 Свойства функции y = tg x Свойства функции y = ctg x y = ctg x y = tg x у π −π −2π 2π x

Геометрические преобразования графиков Преобразование вида y = f(x)+ b Преобразование вида y = f(x – a) Преобразование вида y = kf(x) Преобразование вида y = f(mx) Преобразование вида y = |f(x)| Преобразование вида y = f(|x|) Преобразование вида |y|= f(x)

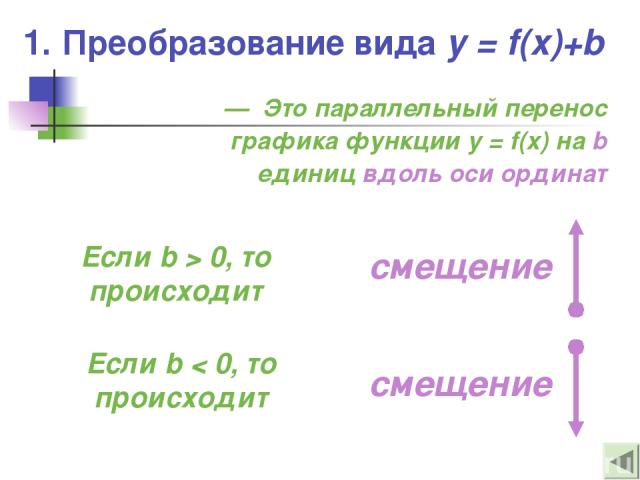
1. Преобразование вида y = f(x)+b — Это параллельный перенос графика функции y = f(x) на b единиц вдоль оси ординат Если b > 0, то происходит Если b < 0, то происходит

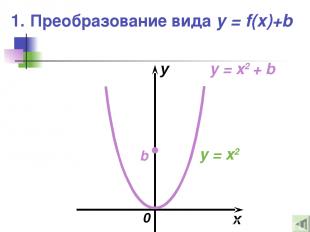
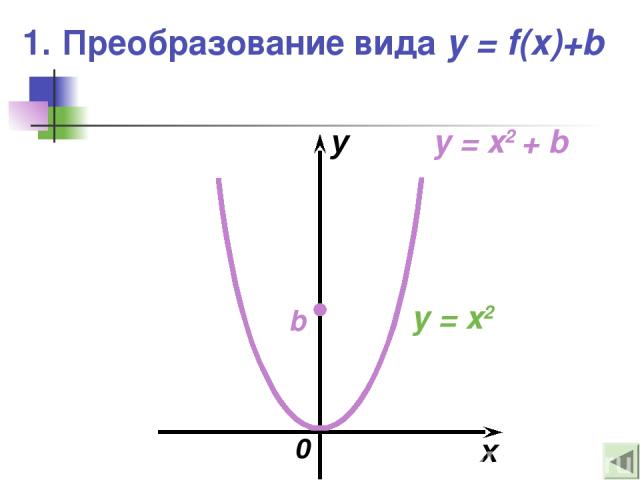
1. Преобразование вида y = f(x)+b x y 0 b y = x2 y = x2 + b

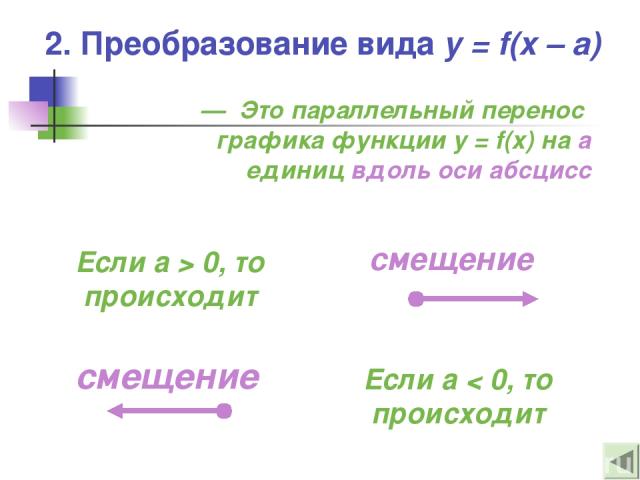
2. Преобразование вида y = f(x – a) — Это параллельный перенос графика функции y = f(x) на а единиц вдоль оси абсцисс Если а > 0, то происходит Если а < 0, то происходит

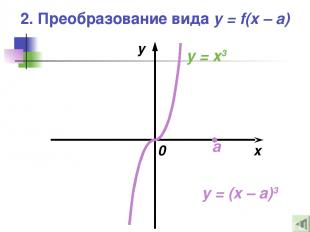
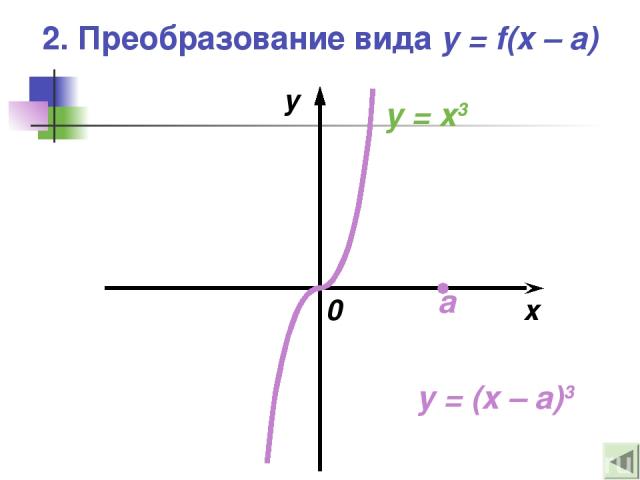
2. Преобразование вида y = f(x – a) x y 0 y = (x – a)3 y = x3 a

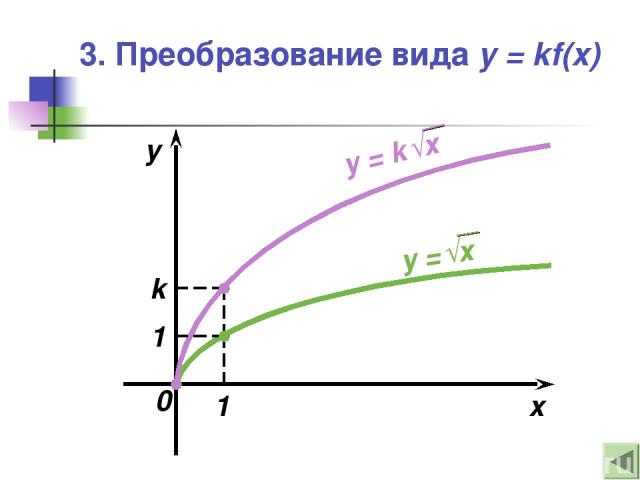
3. Преобразование вида y = kf(x) — Это растяжение (сжатие) в k раз графика функции y = f(x) вдоль оси ординат Если , |k| > 1, то происходит Если , |k| < 1, то происходит

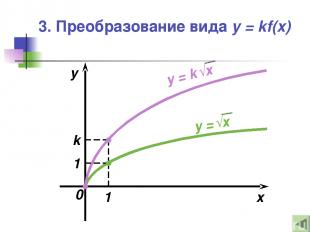
3. Преобразование вида y = kf(x) x y 1 1 k 0

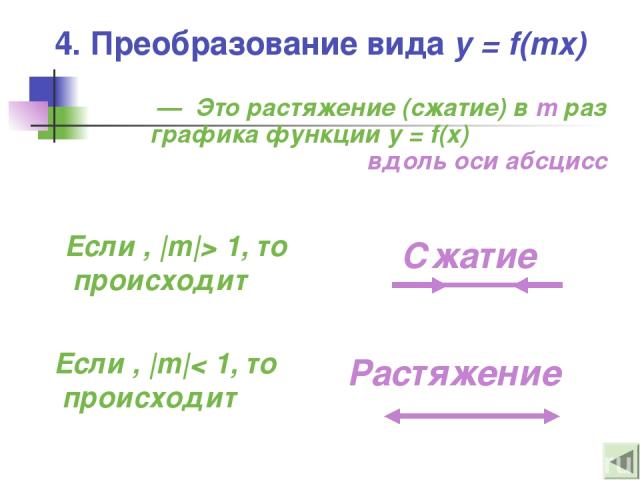
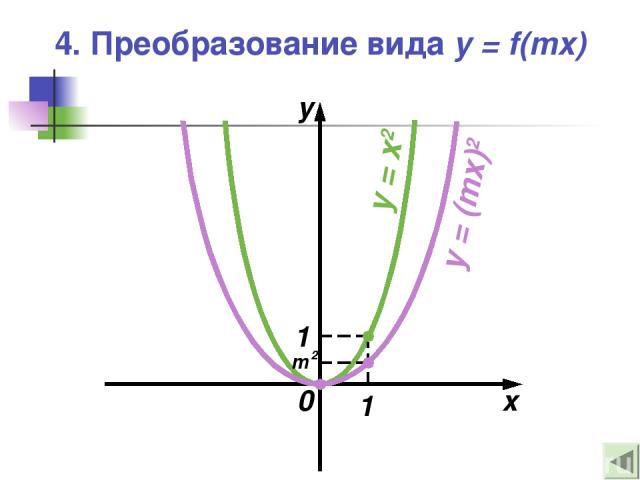
4. Преобразование вида y = f(mx) — Это растяжение (сжатие) в m раз графика функции y = f(x) вдоль оси абсцисс Если , |m|> 1, то происходит Если , |m|< 1, то происходит

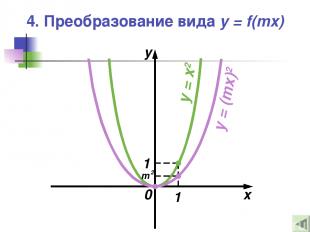
4. Преобразование вида y = f(mx) 0 x y 1 1 y = x2 y = (mx)2

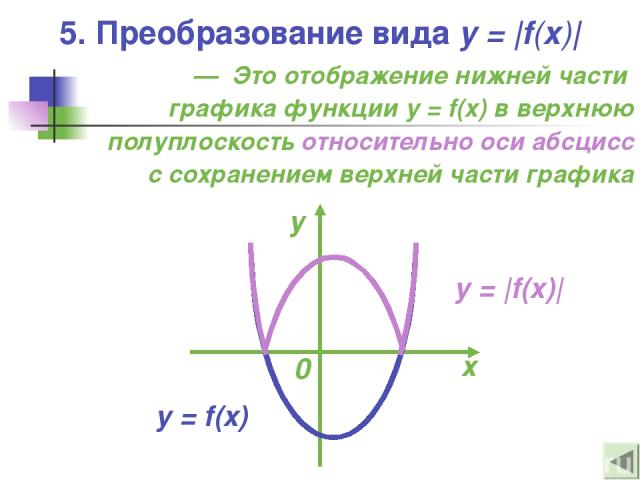
5. Преобразование вида y = |f(x)| — Это отображение нижней части графика функции y = f(x) в верхнюю полуплоскость относительно оси абсцисс с сохранением верхней части графика y = |f(x)|

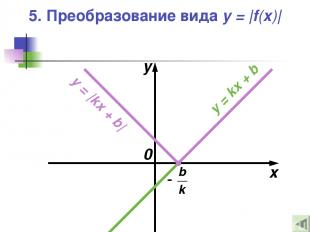
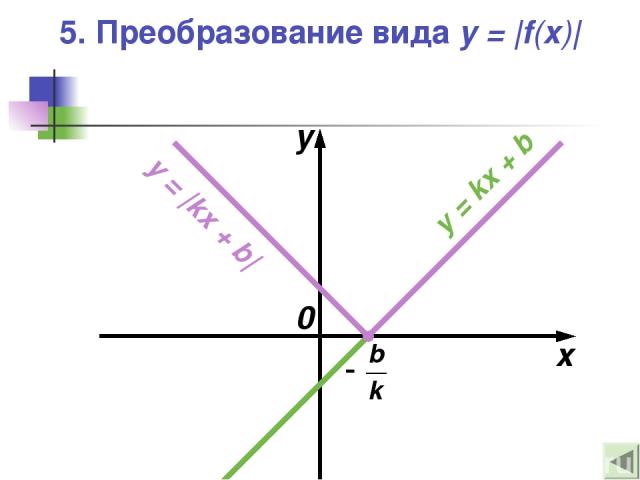
5. Преобразование вида y = |f(x)| x y 0 y = kx + b y = |kx + b|

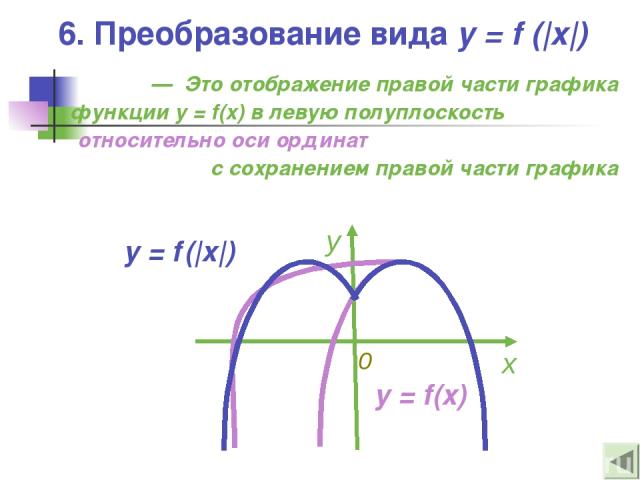
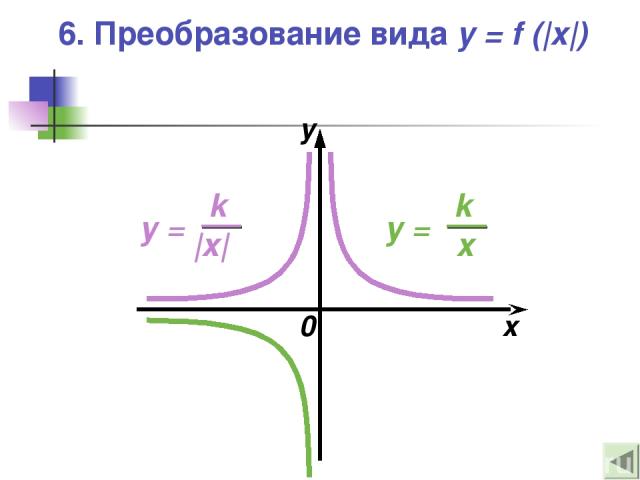
6. Преобразование вида y = f (|x|) — Это отображение правой части графика функции y = f(x) в левую полуплоскость относительно оси ординат с сохранением правой части графика y = f (|x|)

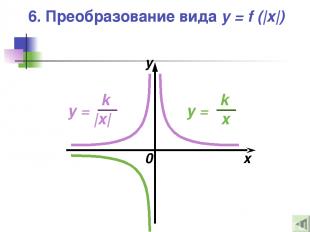
6. Преобразование вида y = f (|x|) 0 x y

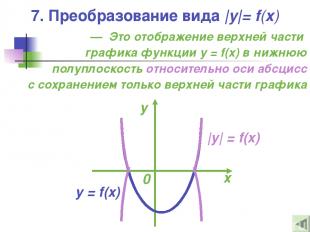
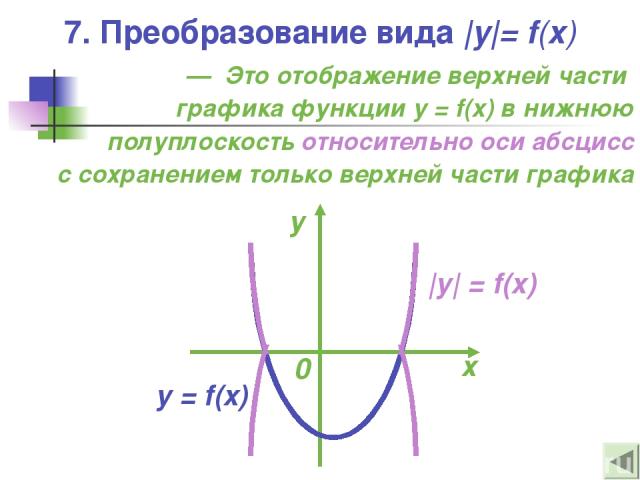
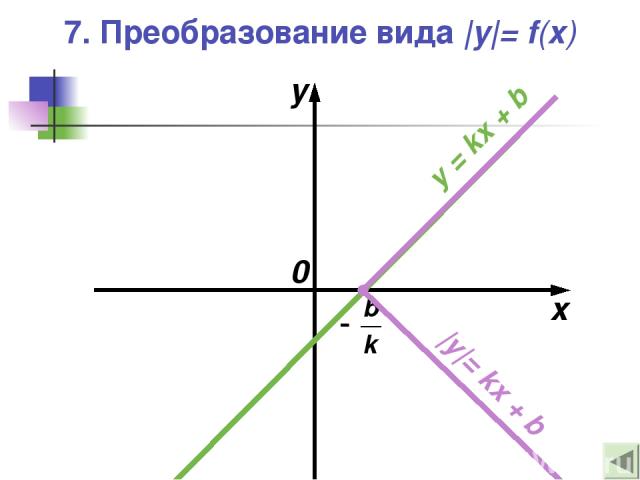
— Это отображение верхней части графика функции y = f(x) в нижнюю полуплоскость относительно оси абсцисс с сохранением только верхней части графика |y| = f(x) 7. Преобразование вида |y|= f(x)

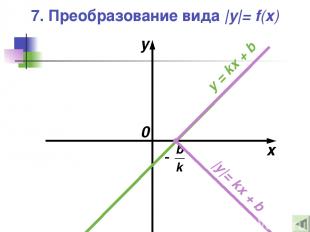
7. Преобразование вида |y|= f(x) x y 0 y = kx + b |y|= kx + b

Свойства функций Свойства линейной функции Свойства квадратичной функции Свойства степенной функции Свойства обратной пропорциональности Свойства показательной функции Свойства логарифмической функции Свойства тригонометрических функций: y = sin x y = tg x y = cos x y = ctg x

Свойства линейной функции 1о D(y) = (−∞; +∞); E(y) = (−∞; +∞). 2о Если b = 0, то функция нечетная. Если b ≠ 0, то функция ни четная, ни нечетная. 3о Если х = 0, то у = b, если у = 0, то х = − . 4о Если k > 0, то функция возрастает при х (−∞; +∞). Если k < 0, то функция убывает при х (−∞; +∞). y = kx + b

Свойства квадратичной функции 1о D(y) = (−∞; +∞). 2о Если a > 0, то E(y) = [ув ; +∞); Если a < 0, то E(y) = (−∞; ув ]. 3о Если b = 0, то функция четная. Если b ≠ 0, то функция ни четная, ни нечетная. 4о Если х = 0, то у = c, если у = 0, то х1,2 = 5о Если a > 0, то функция возрастает при х [xв ; +∞); функция убывает при х (−∞; хв ]. Если a < 0, то функция возрастает при х (−∞; хв ]; функция убывает при х [xв ; +∞). y = ax2 + bx + c, а ≠ 0 Подробнее

Свойства степенной функции y = xn Если n = 2k, где k Z 1о D(y)=(−∞; +∞). 2о E(y)=[0 ; +∞). 3о Функция четная. 4о Если х = 0, то у = 0. 5о Функция возрастает при х [0 ; +∞); убывает при х (−∞; 0]. Если n = 2k +1, где k Z 1о D(y)=(−∞; +∞). 2о E(y)=(−∞; +∞). 3о Функция нечетная. 4о Если х = 0, то у = 0. 5о Функция возрастает при х (−∞; +∞).

Свойства обратной пропорциональности 1о D(y) = (−∞; 0)u(0; +∞) 2о E(y) = (−∞; 0)u(0 ; +∞) 3о Функция нечетная. 4о х ≠ 0, у ≠ 0. 5о Если k > 0, то функция убывает при х (−∞; 0)u(0; +∞). Если k < 0, то функция возрастает при х (−∞; 0)u(0; +∞).

Свойства степенной функции y = x-n Если n = 2k, где k Z 1о D(y)=(−∞; 0)U(0; +∞). 2о E(y)=(0 ; +∞). 3о Функция четная. 4о Если х = 1, то у = 1. 5о Функция возрастает при х (−∞; 0); убывает при х (0 ; +∞). 6º функция ограничена снизу прямой у = 0. Если n = 2k +1, где k Z 1о D(y)=(−∞; 0)U(0; +∞). 2о E(y)=(−∞; 0)U(0; +∞). 3о Функция нечетная. 4о Если х = 1, то у = 1; если х = -1, то у = -1. 5о Функция убывает при х (−∞; 0);(0; +∞). 6º Функция не ограничена

Свойства показательной функции 1о D(y)=(−∞; +∞). 2о E(y)=(0 ; +∞). 3о Функция ни четная, ни нечетная. 4о Если х = 0, то у = 1. 5о Если а > 1, то функция возрастает при х (−∞; +∞). Если 0 < а < 1, то функция убывает при х (−∞; +∞). Подробнее y = ax, а > 0, a ≠ 1

Свойства логарифмической функции y = loga x , а > 0, a ≠ 1 1о D(y)= (0 ; +∞). 2о E(y)= (−∞; +∞). 3о Функция ни четная, ни нечетная. 4о Если х = 1 , то у = 0. 5о Если а > 1, то функция возрастает при х (0; +∞). Если 0 < а < 1, то функция убывает при х (0; +∞). Подробнее

Свойства функции y = sin x 1о D(y)=(−∞; +∞). 2о E(y)=[−1; 1]. 3о Функция нечетная. 4о Если х = 0, то у = 0. 5о Функция возрастает при Функция убывает при 6о Подробнее

Свойства функции y = cos x 1о D(y)=(−∞; +∞). 2о E(y)=[−1; 1]. 3о Функция четная. 4о Если х = 0, то у = 1. 5о Функция возрастает при х [−π+2πn;2πn], n Z. Функция убывает при х [2πn; Π+2πn], где n Z. 6o xmax = 2πn; xmin = π+2πn, где n Z. Подробнее

Свойства функции y = tg x 1о D(y)= где n Z. 2о E(y)=(−∞; +∞). 3о Функция нечетная. 4о Если х = 0, то у = 0. 5о Функция возрастает при х где n Z. 6o Экстремумов нет. Подробнее

Свойства функции y = ctg x 1о D(y)=(πn; π+πn), где n Z 2о E(y)=(−∞; +∞). 3о Функция нечетная. 4о х ≠ 0; у = 0 если х , где n Z. 5о Функция убывает при х (πn; π+πn), где n Z. 6o Экстремумов нет. Подробнее