Презентация на тему: ГРАФИЧЕСКОЕ РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ

ГРАФИЧЕСКОЕ РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ Урок формирования умений и навыков

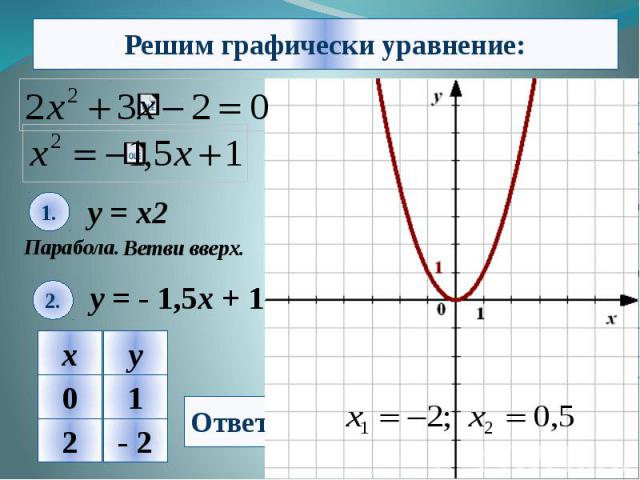
Вопросы: 1.Что является графиком функции у=х+3? Ответ: графиком функции у=х+3 является прямая. 2. Какая кривая является графиком функции у=0,5х2 ? Ответ: графиком функции у=0,5х2 является парабола. 3. Куда направлены ветви параболы? Почему? Ответ: ветви параболы направлены вверх, т.к. а 0, а=0,5. 4. Что является графиком функции у=6/х ? Ответ: графиком данной функции является гипербола. 5. В каких четвертях расположены ветви гиперболы у=-? Ответ: ветви гиперболы расположены во 2 и 4 четвертях. 6. Что является графиком функции у= Ответ: ветвь параболы.

7. В каких четвертях расположен график функции у=? 7. В каких четвертях расположен график функции у=? Ответ: в 3 и в 4 координатных четвертях. 8. Найти координаты вершины параболы (х0;у0), заданной формулой у=х2+2х-3. Ответ: х0=-2:2=-1.у0=(-1)2-2-3=-4,то есть (-1;-4;). 9. Какая прямая служит осью симметрии параболы: у=х2+2х-3? Ответ: осью симметрии параболы служит прямая х=х0, то есть прямая х=-1. 10. Определите наименьшее значение функции: у=х2+2х-3. Ответ: наименьшее значение функции равно -4. 11. Укажите промежутки возрастания и убывания функции: у=х2+2х-3. Ответ: функция у=х2+2х-3 убывает на промежутке (-;-1], функция возрастает на промежутке [-1;+
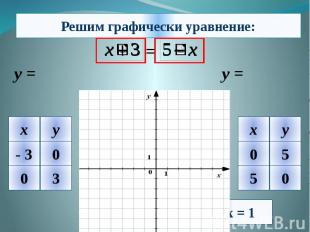

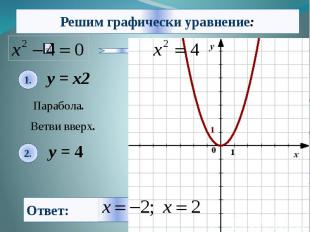
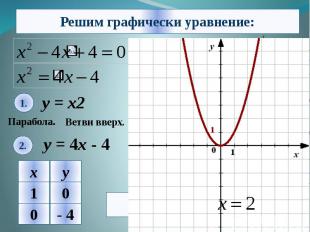
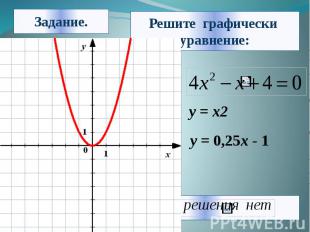
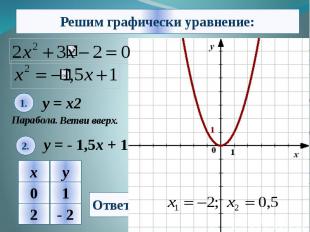
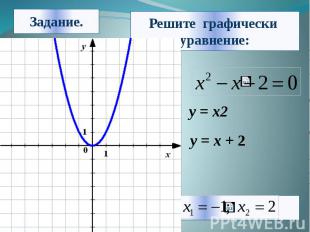
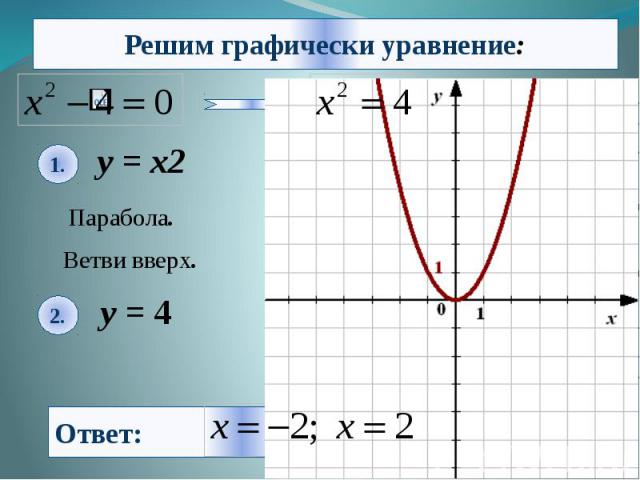
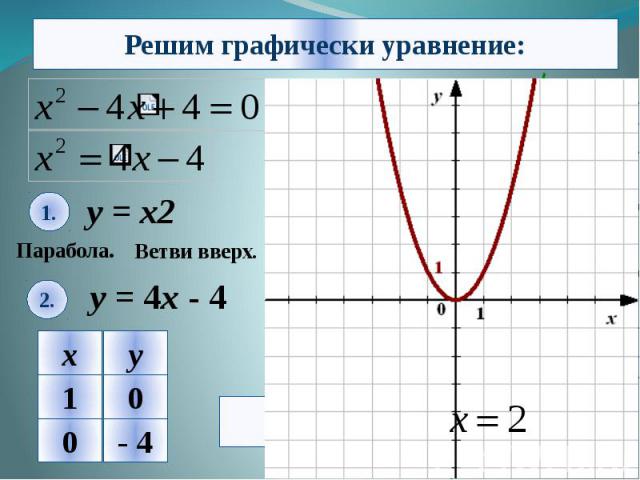
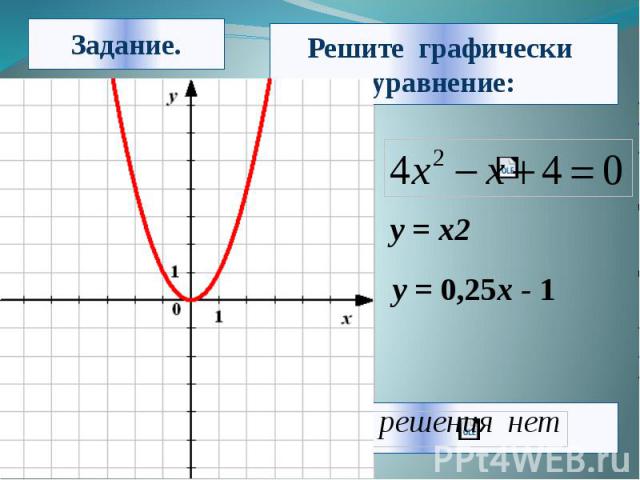
Алгоритм решения: 1. Из уравнения выделяем знакомые нам функции. 2. Строим графики функций в одной координатной плоскости. 3. Находим координаты точек пересечения графиков. 4. Из найденных координат-выбираем значение абсциссы ,то есть х. 5. Записываем ответ.