Презентация на тему: Что такое функция?

Ознакомиться с понятием «функция», закрепить его на примерах Ознакомиться с понятием «функция», закрепить его на примерах Усвоить новые термины: зависимая переменная и независимая переменная (аргумент функции и значение функции). Узнать способы задания функции. Закрепить их при решении задач

Никакое другое понятие не отражает Никакое другое понятие не отражает явлений реальной действительности с такой с такой конкретностью, как понятие функциональной зависимости

зависимость

Площадь квадрата зависит от длины его стороны. Если изменить длину стороны квадрата, то изменится и значение площади. S = aa Если а=3, то S=3*3=9(ед кв) Если а=0,4, то S=0,4*0,4 = 0,16(ед кв)

Периметр квадрата зависит от длины его стороны Периметр квадрата зависит от длины его стороны Длина окружности зависит от длины его радиуса Пройденный путь зависит от его скорости Длина стального стержня зависит от его температуры Давление масла зависит от высоты столба масла Ваши примеры

Р = 4а ( р зависит от а) Р = 4а ( р зависит от а) С=2пR (с зависит от R) S = t v ( s зависит от v ) Если переменные а, R , v обозначить буквой х, а переменные P, C, S обозначить буквой у, то получатся формулы звисимостей у от х .

а (длина стороны) а (длина стороны) Аргумент функции Независимая переменная

В таблице показана зависимость количества выпущенных заводом электроплит от порядкового номера месяца, в котором были выпущены электроплиты В таблице показана зависимость количества выпущенных заводом электроплит от порядкового номера месяца, в котором были выпущены электроплиты

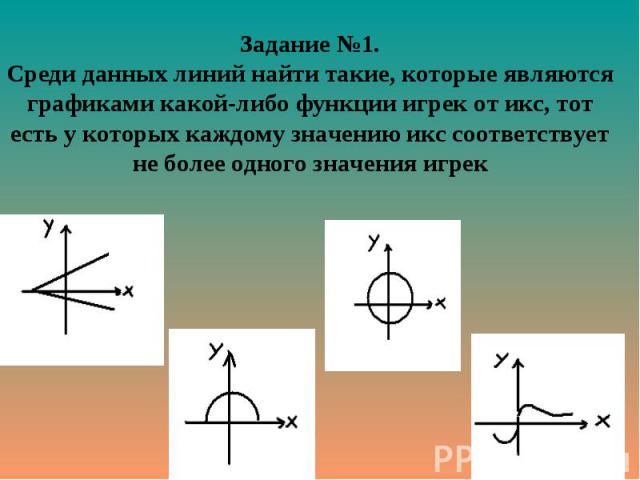
Функцией называют такую зависимость Функцией называют такую зависимость переменной у от переменной х, при которой каждому значению х соответствует единственное значение у

Термин «функция» - от латинского functio - совершение, выполнение Термин «функция» - от латинского functio - совершение, выполнение Первоначально понятие функции как выражения сложилось в 17 веке В 18 веке основным объектом изучения математики стали зависимости между переменными величинами Впервые термин функция ввёл И.Бернулли в 1718 году В общем виде определение функции было дано Н.И. Лобачевским в 1934 г.

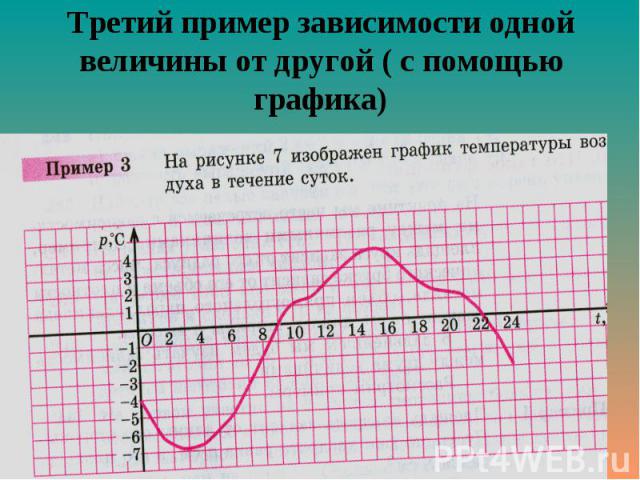
С помощью формулы. У = - 4х + 5 С помощью формулы. У = - 4х + 5 С помощью таблицы С помощью графика

Как вы поняли, что такое функция? Как вы поняли, что такое функция? Приведите два примера зависимости одной величины от другой Какими способами может быть задана функция? Как иначе можно назвать независимую переменную ? Как иначе можно назвать зависимую переменную? Выполни задание на слайде №18.