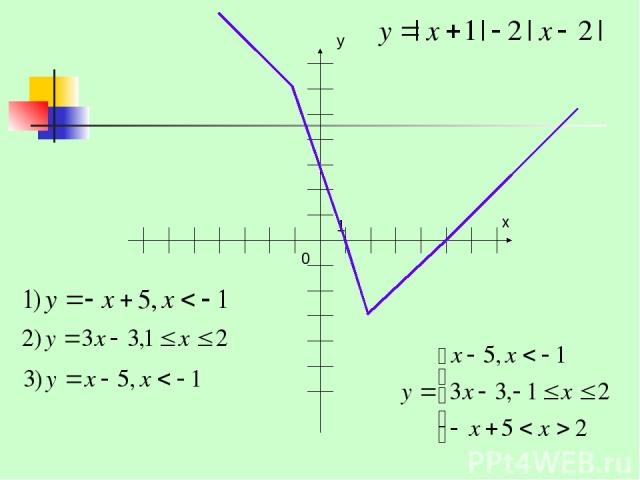
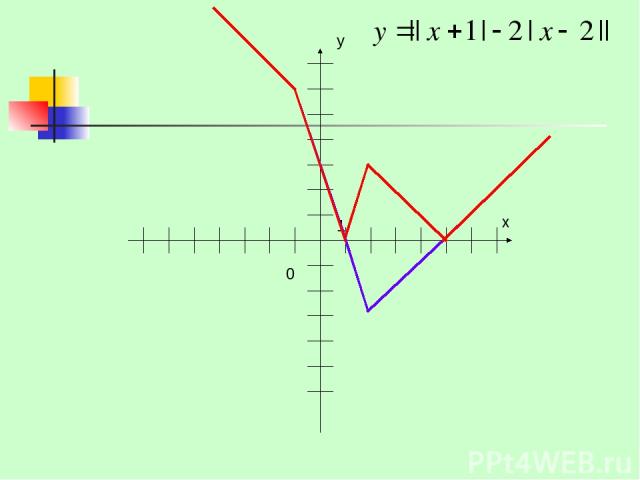
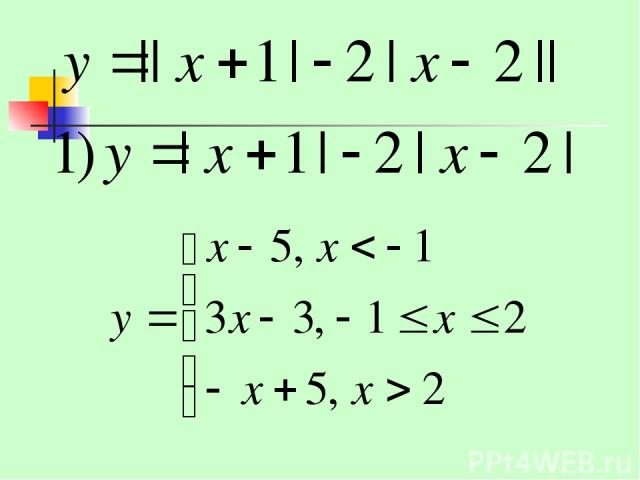Презентация на тему: Графическое решение неравенств

«Применение графического и функционально-графического методов к решению неравенств » Урок математики в 9 академическом классе 28 ноября 2008 года Учитель: Алтухова Ю.В. Брянский городской лицей №1 имени А.С.Пушкина 5klass.net

Математика – наука молодых. Иначе и быть не может. Занятия математикой – это такая гимнастика ума, для которой нужны вся гибкость и вся выносливость молодости. Норберт Винер (1894-1964), американский ученый

отношение между числами a и b (математическими выражениями), соединенное знаками Неравенство -

Историческая справка Задачи на доказательство равенств и неравенств возникли в глубокой древности . Для обозначения знаков равенства и неравенства использовали специальные слова или их сокращения. IV век до н.э., Евклид, V книга «Начал»: если a, b, c, d – положительные числа и a – наибольшее число в пропорции a/b=c/d, то выполняется неравенство a+d=b+c. III век , основной труд Паппа Александрийского «Математическое собрание»: если a, b, c, d – положительные числа и a/b>c/d, то выполняется неравенство ad>bc. Более 2000 лет до н.э. было известно неравенство Обращается в верное равенство при a=b.

Современные специальные знаки 1557 год. Введен знак равенства = английским математиком Р.Рикордом. Его мотив: «Никакие два предмета не могут быть более равными, чем два параллельных отрезка». 1631 год. Введены знаки > и < английским ученым Харритом в книге «Практика аналитического искусства». 1734 год. Знаки введены французским математиком П.Буге.

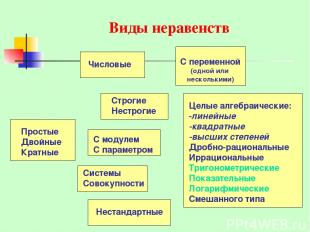
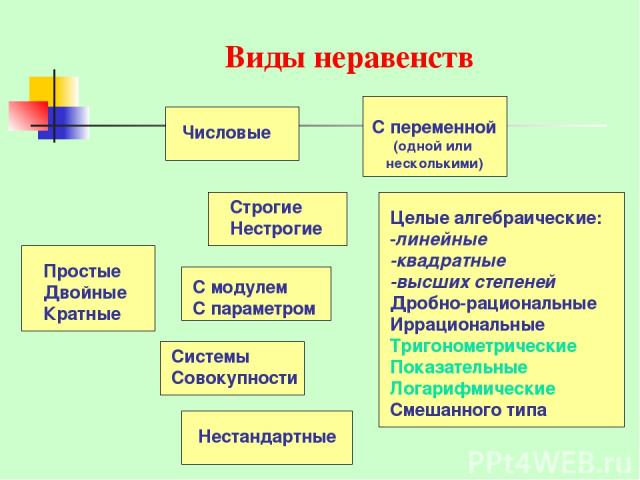
Виды неравенств

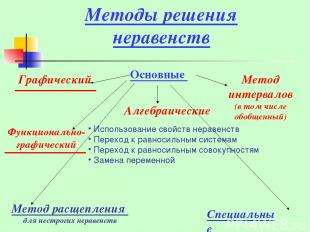
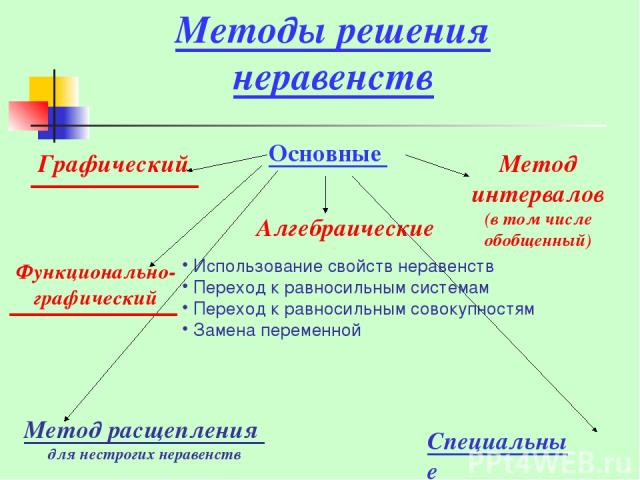
Методы решения неравенств Графический Основные Специальные Функционально- графический Использование свойств неравенств Переход к равносильным системам Переход к равносильным совокупностям Замена переменной Метод интервалов (в том числе обобщенный) Алгебраические Метод расщепления для нестрогих неравенств

называется значение переменной, которое при подстановке обращает его в верное числовое неравенство. Решить неравенство – найти все его решения или доказать, что их нет. Два неравенства называются равносильными, если все решения каждого являются решениями другого неравенства или оба неравенства решений не имеют. Неравенства Решением неравенства с одной переменной

Охарактеризуйте неравенства. Решите устно   3) (x – 2)(x + 3)   0

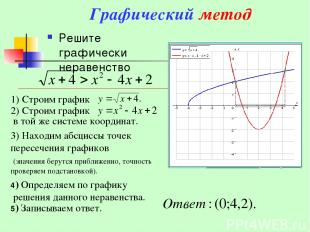
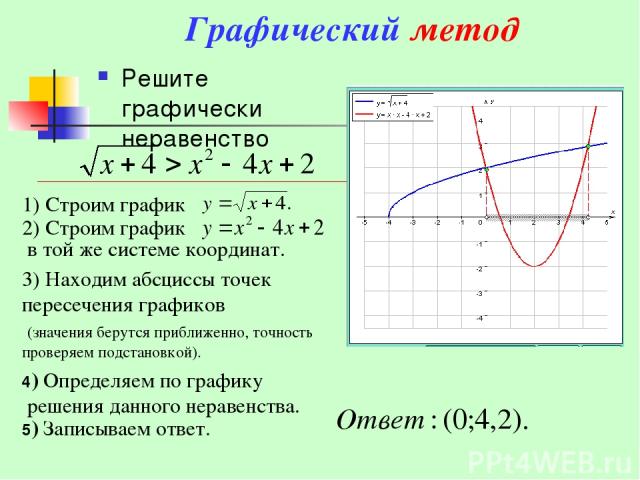
Графический метод Решите графически неравенство 3) Находим абсциссы точек пересечения графиков (значения берутся приближенно, точность проверяем подстановкой). 4) Определяем по графику решения данного неравенства. 5) Записываем ответ.

Функционально-графический метод решения неравенства f(x) < g(x) : 1. Подбором найдем корень уравнения f(x)=g(x), используя свойства монотонных функций; 2. Построим схематически графики обеих функций, проходящие через точку с найденной абсциссой; 3. Выберем решение неравенства, соответствующее знаку неравенства; 4. Запишем ответ.

Функционально-графический метод Решите неравенство: 3) Уравнение f(x)=g(x) имеет не более одного корня. Решение. 4) Подбором находим, что х=2. II. Схематически изобразим на числовой оси Ох графики функций f(x) и g(x), проходящие через точку х=2 . III. Определим решения и запишем ответ. Ответ. х -7 не определена 2

Решите неравенства:

Построить графики функции ЕГЭ-9, 2008 год

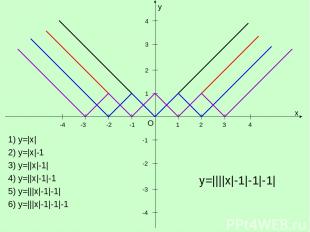
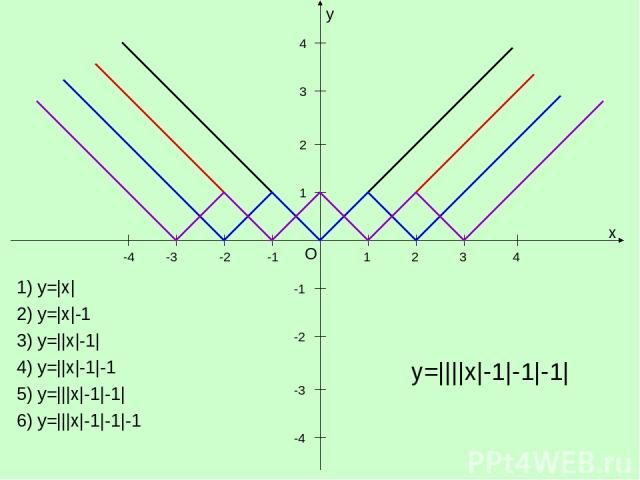
y x O 1 1 -1 -1 -2 -3 -4 2 3 4 -2 -3 -4 2 3 4 1) y=|x| 2) y=|x|-1 3) y=||x|-1| 4) y=||x|-1|-1 5) y=|||x|-1|-1| 6) y=|||x|-1|-1|-1 y=||||x|-1|-1|-1|

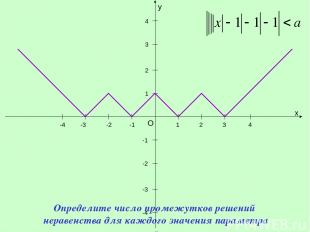
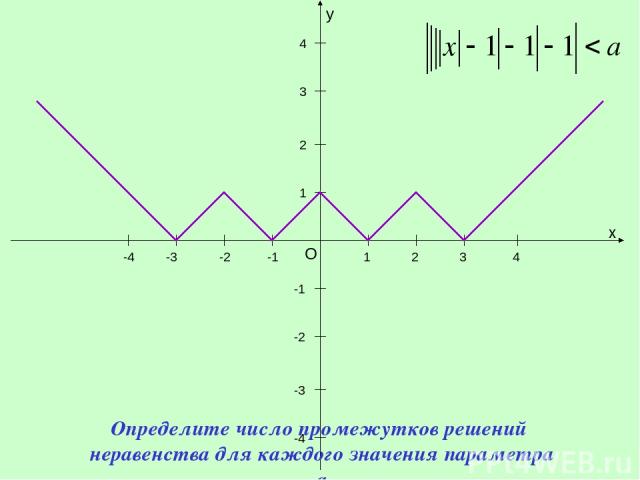
y x O 1 1 -1 -1 -2 -3 -4 2 3 4 -2 -3 -4 2 3 4 Определите число промежутков решений неравенства для каждого значения параметра a

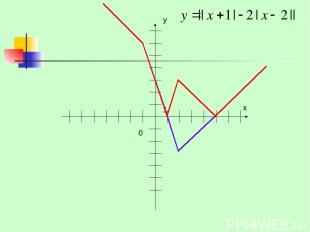
Построить график функции ЕГЭ-9, 2008 год

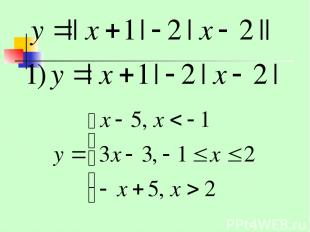
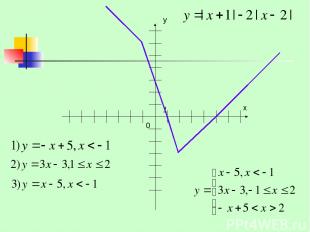
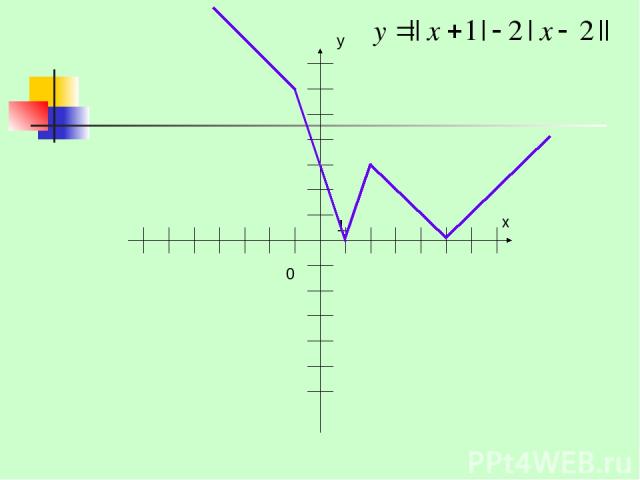
0

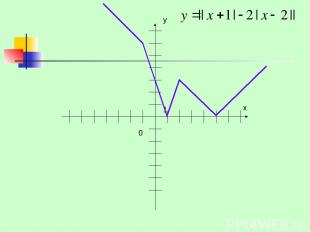
0

0

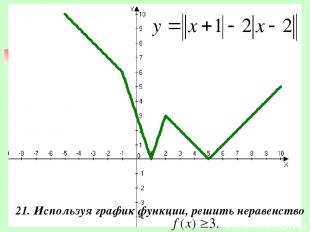
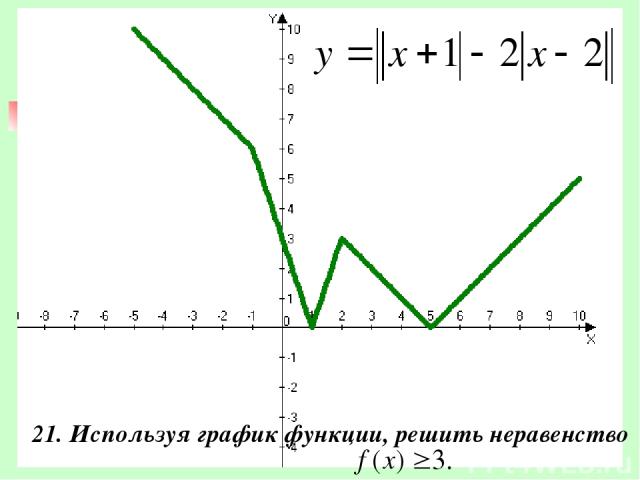
21. Используя график функции, решить неравенство

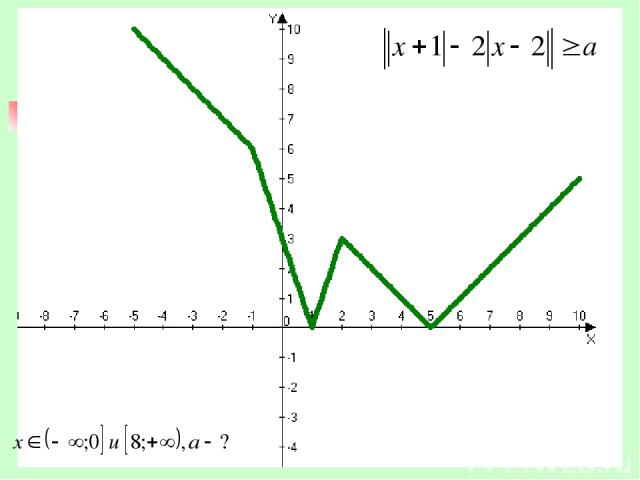
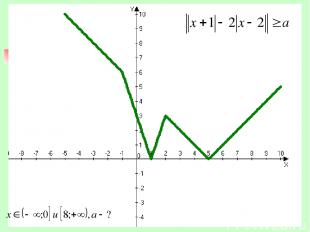
При каких значениях параметра а решением неравенства является объединение промежутков

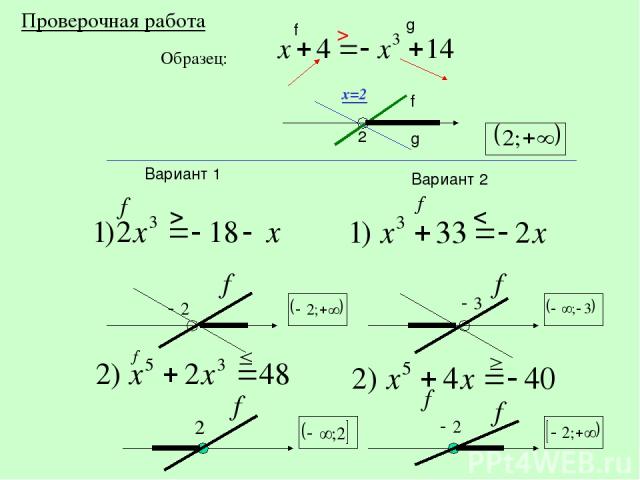
Образец: x=2 Проверочная работа Вариант 1 Вариант 2 > 2 f g g f

Образец: x=2 Проверочная работа Вариант 1 Вариант 2 > 2 f g g f

Домашнее задание /Г/, № 8.184 (б) В каждом уравнении поставить любой знак неравенства и решить полученное неравенство