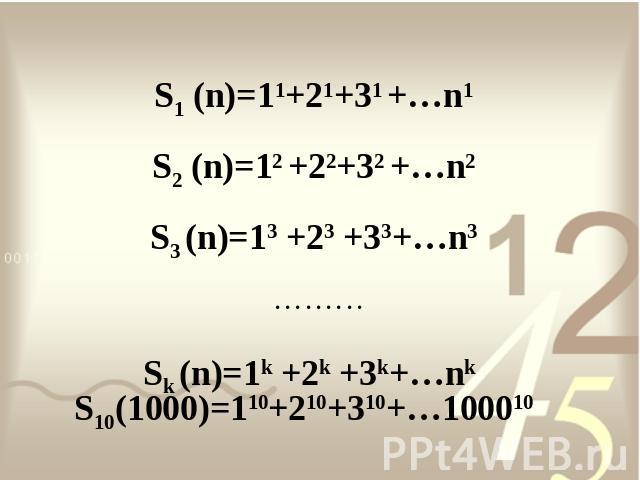Презентация на тему: Числа Бернулли

Числа Бернулли

«Прогресс науки определяется трудами ее ученых и ценностью ее открытий» Л.Пастер

Числа Бернулли. «Прогресс науки определяется трудами ее ученых и ценностью их открытий» Л.ПастерТеория чисел — раздел математики, занимающийся изучением чисел как таковых так и их свойств и поведения в различных ситуациях. Как сказал великий математик Пифагор "Все есть число!“ Изучая числа мы изучаем окружающий нас мир и себя в том числе. С древних времен математики пытались постичь тайны удивительного мира чисел. Этот мир привлекает своим многообразием, строгостью и совершенством законов. Здесь есть «великаны» и есть «карлики», обычные «трудяги» и такие «знаменитости», как π и e.

Но еще более многообразен мир числовых последовательностей. Здесь и последовательность натуральных чисел и полная глубоких тайн последовательность простых чисел и последовательность “биноминальных коэффициентов”…В моей работе речь пойдет об одной замечательной последовательности чисел, которую открыл выдающийся швейцарский математик Якоб Бернулли (1654—1705).Последовательность эта играет в математике важную роль, что объясняется ее связью с вопросами суммирования функций, простыми числами, великой теоремой Ферма, а также другими задачами.

Якоб Бернулли (27 декабря 1654 - 16 августа 1705)профессор математики Базельского университета (с 1687). Из семьи Бернулли. Отец Бернулли занимал в городе заметное положение, был членом городского суда и членом Большого городского совета. Отец прочил Якоба в священнослужители, и ему пришлось изучать в университете философию, богословие и языки. Отец не допускал отступления от намеченного плана, поэтому Якоб вынужден был заниматься математикой тайком, без учителя и почти без учебников. Обучение в университете шло своим чередом, и в 1671г. он получил степень магистра философии. В 1676 Якоб отправился в длительное путешествие, из которого возвратился только в 1680г. Он посетил некоторые города Швейцарии, Италию, Францию.

По возвращении в Базель Якоб опубликовал в 1681 и 1682 две работы: одна содержала рассуждения о природе комет, другая - о тяжести эфира. Наиболее значительные достижения Якоба I в развитии анализа бесконечно малых, теории рядов, вариационного исчисления и теории вероятностей. В 1687, ознакомившись с первым мемуарам Г.Лейбница по дифференциальному исчислению (1684), применил новые идеи к изучению свойств ряда кривых: логарифмические спирали, открытой им лемнискаты, цепной линии и др.В труде "Искусство предложения" Якоб I в 1713 решил некоторые задачи комбинаторики; открыл числа, позднее названные числа Бернулли; доказал так называемую теорему Бернулли - частный случай закона больших чисел, имеющего большое значение в теории вероятностей и ее приложениях к статистике; построил математическую модель для описания серии независимых испытаний (схема Бернулли). Благодаря его работам теория вероятностей приобрела важнейшее значение в практической деятельности.

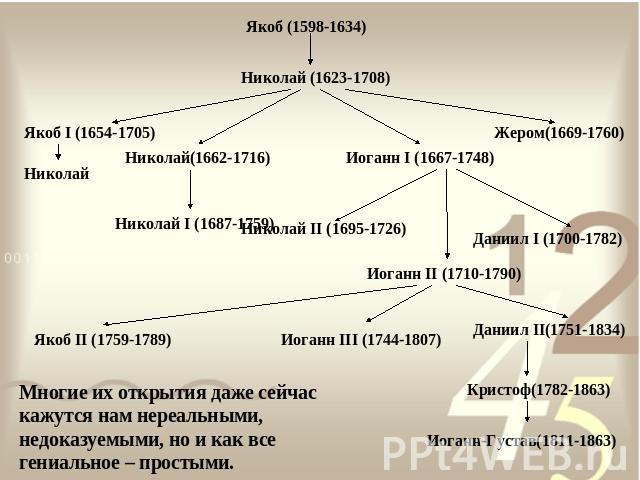
Династия БернуллиБЕРНУЛЛИ - династия швейцарских ученых родом из Антверпена, бежавших из города после захвата его испанцами и поселившихся в 1622 году в Базеле. По крайней мере восемь ее представителей оставили заметный след в истории точных наук. Среди академиков Петербургской Академии наук — пятеро представителей семьи Бернулли.Примечательно не то, что это семейство сделало ряд значимых открытий в разных областях науки, а то, что они, за исключением только некоторых членов семьи, были как-либо связаны с наукой, в частности с математикой

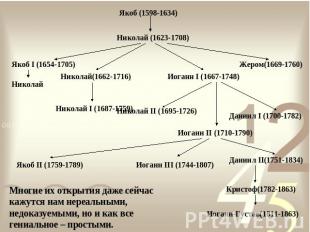
Многие их открытия даже сейчас кажутся нам нереальными, недоказуемыми, но и как все гениальное – простыми.

Запись чисел. Натуральные числа возникли в глубокой древности как результат счета различных предметов: людей, животных, птиц, деревьев, орудий труда и т.д. Ряд натуральных чисел: 1, 2, 3, 4, 5, … является бесконечным и называется натуральным рядом. При изучении свойств чисел Я. Бернулли встретился с суммированием степеней натуральных чисел Эти вопросы интересовали математиков и ранее. Я. Бернулли составил таблицу фигурных чисел, указал их свойства и на основании отмеченных свойств нашел формулы для сумм степеней натуральных чисел. Он привел формулы для сумм от S(n) до S(n10):

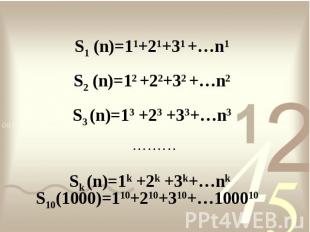
Найдем обобщенную формулу для вычисления этих сумм.1) Обозначим эти суммы следующим символом: S.2) Возведем числа (от первого числа до числа n) этих сумм в степень.3) С помощью разложения:Которое мы получили при последовательном возведении двучлена (бинома) a+b первую, вторую, третью, … степениa+b=1·a+1·b(a+b)2=1·a2+2·ab+1·b2(a+b)3=1·a3+3·a2b+3·ab2+1·b3(a+b)4=1·a4+4·a3b+6·a2b2+4·ab3+1·b4напишем тождество:

Из которого легко получить сумму Sk(n), если известно S1(n), S2(n),…Sk-1(n)Например, проверим, что

Числа Бернулли — последовательность рациональных чисел B0 ,B1 ,B2 ,... найденная Я. Бернулли в связи с вычислением суммы одинаковых степеней натуральных чисел.Из формулы S1 (n), S2 (n), S3(n) следует что, В0=1, B1= , B2= , B3=0Из определения и рекуррентного соотношения вытекает простой способ вычисления чисел Бернулли. Из следующей формулы мы можем вычислить Bk

C помощью этой формулы можно проверить значения первых четырех чисел Бернулли. Я проверю значение B4

Бернулли удалось доказать, что и другие коэффициенты многочлена Sk(n) вычисляются с помощью чисел Вk.Коэффициент при n2 оказывается равным ,коэффициент при n3 равен ,наконец, коэффициент при степени nk оказывается не зависящим от k и всегда равным Таким образом, формула Бернулли имеет вид

Вычислим с помощью этой формулы S5(n) следующим образомЗа счет этой формулы мы с легкостью можем высчитать сумму степеней любого числа, например;

Для чего же нам нужны числа Бернулли?Изучая этот материал я выяснила, что числа Бернулли не зря используются в математических анализах и в теории чисел. Они помогают очень быстро вычислить сумму степеней любого числа а также разложить некоторые элементарные функций в степенные ряды.