Презентация на тему: Пространственная теорема Пифагора

Пространственная теорема Пифагора

Все плоские углы тетраэдра ОABC при вершине О — прямые. Докажите, что квадрат площади треугольника ABC равен сумме квадратов площадей остальных граней (пространственная теорема Пифагора).

Три формулировки теоремы Пифагора: В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов;Квадрат длины диагонали прямоугольника равен сумме квадратов длин двух его взаимно перпендикулярных сторон;Квадрат длины любого отрезка равен сумме квадратов длин его проекций на любые две взаимно перпендикулярные прямые.

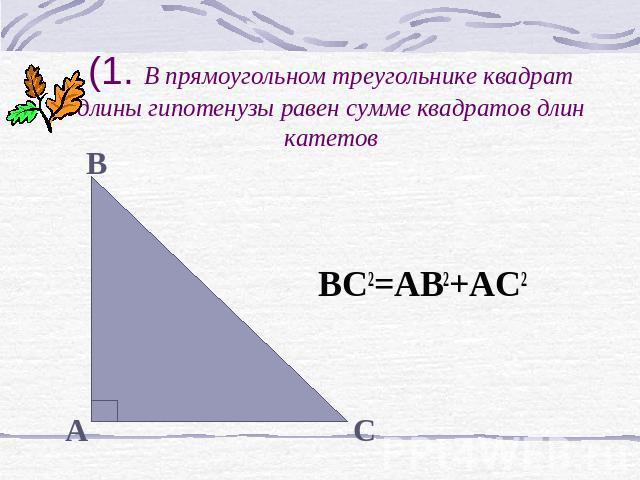
BC2=AB2+AC2 (1. В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов

2.Квадрат длины диагонали прямоугольника равен сумме квадратов длин двух его взаимно перпендикулярных сторон B1 OC2=OA2+OB2 OA=O1A1 OB=O2B1

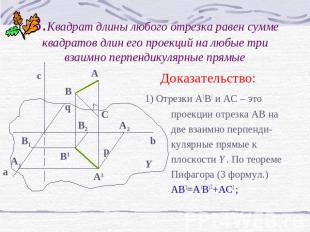
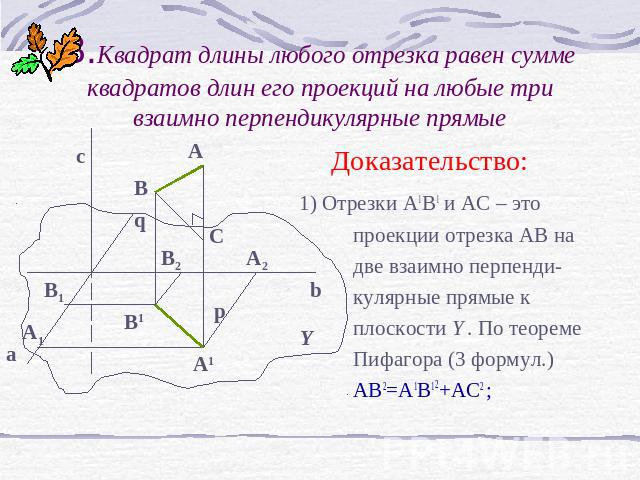
3.Квадрат длины любого отрезка равен сумме квадратов длин его проекций на любые три взаимно перпендикулярные прямые Доказательство: 1) Отрезки A1B1 и AC – это проекции отрезка АВ на две взаимно перпенди- кулярные прямые к плоскости Y. По теореме Пифагора (3 формул.) AB2=A1B12+AC2 ;

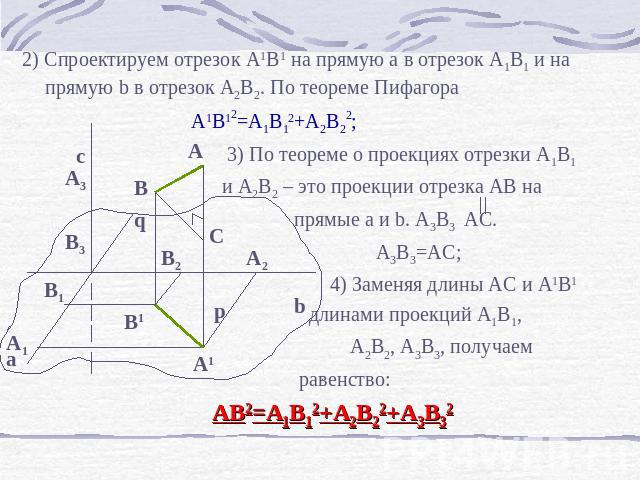
2) Спроектируем отрезок A1B1 на прямую а в отрезок А1В1 и на прямую b в отрезок А2В2. По теореме Пифагора A1B12=A1B12+A2B22; 3) По теореме о проекциях отрезки А1В1 и А2В2 – это проекции отрезка АВ на прямые a и b. А3В3 АС. А3В3=АС; 4) Заменяя длины АС и А1В1 длинами проекций А1В1, А2В2, А3В3, получаем равенство: AB2=A1B12+A2B22+A3B32

Всегда хочется быть выше перед страхом казаться неумелым… Будь уверен в себе все получится!!! Автор: Марко Анна