Презентация на тему: Площадь круга и кругового сектора

Площадь круга и кругового сектора МОУ СОШ № 256 г.Фокино.

Цели урока: Дать представление о выводеформулы площади круга и на ееоснове получить формулу площадикругового сектора. Научиться решать задачи на применение формул площади круга и кругового сектора.

Проверка выполнения домашнего задания: Что означает один оборот колеса с математической точки зрения? 2) Чему равно расстояние, пройденное автомобилем, если колесо автомобиля сделало один оборот? Ответ: 0,63 м.

Задача № 1111. Что нужно знать для вычисления длины дуги? Каким образом можно вычислить радиус камня? Ответ: ≈ 59,189 (см)

Самостоятельная работа: 1 вариант. 2 вариант.

Площадь круга. Часть плоскости, Ограниченная окружностью.

Площадь круга. А1А2…Ап – правильный п – угольник с площадью Sn. Окр. (О; R) – окружность с площадью S, описанная около многоугольника. Окр. (О; r) – окружность с площадью S2 , вписанная в многоугольник. S2 < Sn < S.
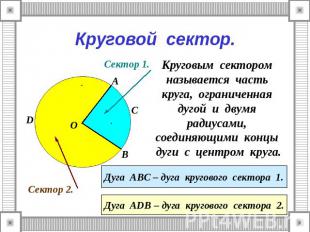
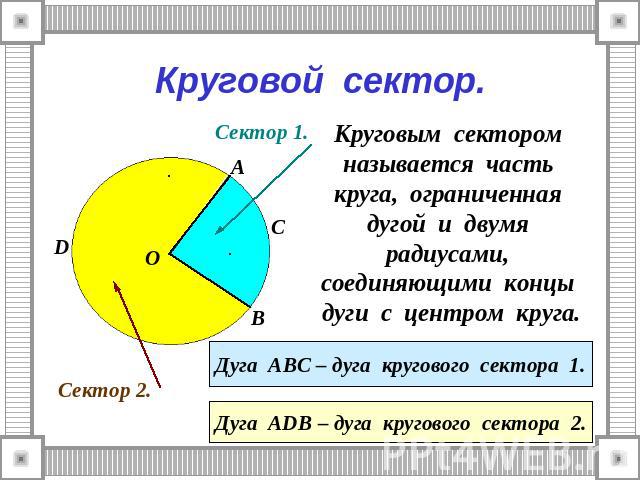
Круговой сектор. Круговым сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга. Дуга АВС – дуга кругового сектора 1. Дуга АDВ – дуга кругового сектора 2.

Площадь кругового сектора. S = πR2Удачи в решении задач!

Задачи: № 1Диаметр основанияЦарь-колокола, находящегосяв московском Кремле, равен 6,6 м. Найдите площадь основания колокола. № 2.Длина окружностицирковой арены равна 41 м. Найдите диаметр и площадь арены.

Задача № 3: Из круга, радиус которого 10 см, вырезан сектор с дугой в 600. Найдите площадь оставшейся части круга.

Домашнее задание: Пп. 111; 112.№ 1114; 1120; 1127.