Презентация на тему: Развитие творческой активности учащихся на уроках математики

Тема самообразования:«Развитие творческой активности учащихся на уроках математики»

Цель: выявить эффективные приемы и способы развития творческих способностей школьников на уроке математики.

Тема урока: «Линейные уравнения с одной переменной». Девиз: «Смотреть – не значит видеть!»28k + 30n + 31m = 365k=? n=? m=?

Реши уравнение:(3х+7)*2 – 3 = 176х+14 – 3=176х=17 – 4 -36х=0х=0?

Реши уравнение: 28k+30n+31m=365k=? n=? m=?Подсказка: 365- это количество дней в году,…

Проверка домашнего задания Задание. Начертить в тетради любой треугольник и с помощью транспортираизмерить его углы, и найти их сумму.Какие суммы вы получили?

Вопрос: Случайно ли сумма углов данного треугольника АВС оказалось равной 180º или этим свойством обладают все треугольники?

Практическая работа Построить треугольник по заданным углам: 1.<A=37º, <B=28º, <C=90º 2.<A=72º, <B=50º, <C=110º 3.<A=23º, <B=50º, <C=38º. Всегда ли можно построить треугольник?

Гипотеза:треугольник можно построить, если сумма внутренних углов его равна 180º. На рис. прямые ВD и АС парал-лельны.Найдите сумму углов △ АВС.

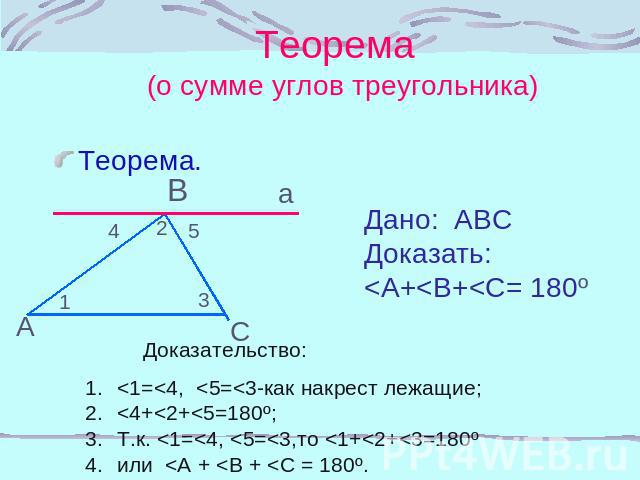
Теорема (о сумме углов треугольника) Теорема. Дано: АВС Доказать:<A+<B+<C= 180º Доказательство: <1=<4, <5=<3-как накрест лежащие;<4+<2+<5=180º;Т.к. <1=<4, <5=<3,то <1+<2+<3=180ºили <A + <B + <C = 180º.

Правильно ли поставлены размеры на чертеже? Если нет, то укажите ошибку. Какие знания потребовались для ответа на вопрос?

Вычисление длины окружности На глиняных табличках, найденных в Месопотамии и датированных началом II тысячелетия до нашей эры, можно прочесть: «Если 60 есть окружность, то третья часть от 60 представляет собой 20. Это и есть диаметр.» Из этого следует, что отношение длины окружности к диаметру считалось величиной постоянной и равной 3. Это число назвали π (пи)

Слово «симметрия» греческого происхождения («сим» - с, «метрон» - мера) и буквально означает «соразмерность» «Симметрия есть идея, с помощью которой человек веками пытался постичь и создать порядок, красоту и совершенство» Герман Вейль.

Центральная симметрия АО = ОВ

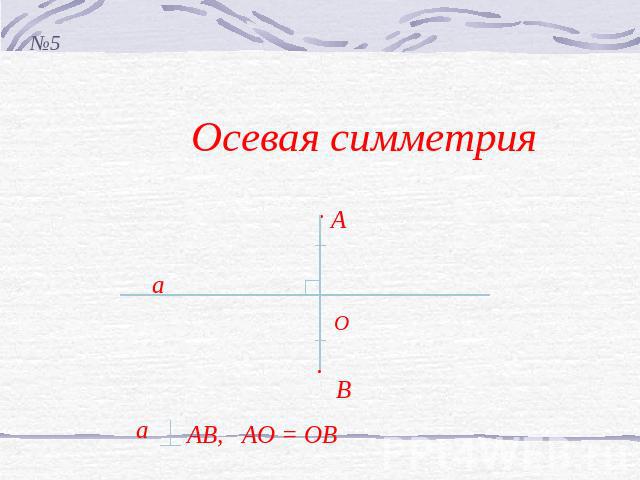
Осевая симметрия АВ, АО = ОВ

Орнамент «Искусство орнамента содержитв неявном виде наиболее древнюю часть известной нам высшей математики» Г. Вейль


РЕШЕНИЕ УРАВНЕНИЙ ГРАФИЧЕСКИМ СПОСОБОМ («Функции и графики», материалы ЕГЭ, часть «В») Пусть дано уравнение f (x) = g (x).Строим графики функций левой и правой частей уравнения у = f (x) и у = g (x).Находим точки пересечения графиков. Абсциссы точек пересечения и есть решения данного уравнения.

Решить уравнение: 2 способ (графический) 1. левая часть уравнения неотрицательна при любом значении неизвестной х, . 2. при уравнение примет вид , и имеет корень х =0 . 3. при находим корни уравнения по формуле

« Математике нельзя научиться , глядя как это делает сосед! » А.Нивен. №1. При каких значениях параметра а уравнение имеет одно решение ? №2. При каких значениях параметра а уравнение не имеет решений ?

При каких значениях параметра а уравнение имеет одно решение ? Запишем уравнение в виде: Построим графики функций: и подвижную прямую у = а. Ответ: а =3

При каких значениях параметра а уравнение не имеет решений ? Построим график и прямую у = а. По рисунку видим при решений нет. Ответ:

ВЫВОД (Графический способ решения задач с параметром) Задачу с параметром можно рассматривать как функцию f (x; a) =0 1. Строим графический образ 2. Пересекаем полученный график прямыми параллельными оси абсцисс 3. «Считываем» нужную информацию Схема решения: