Презентация на тему: Построение некоторых типов нелинейных моделей

Построение некоторых типов нелинейных моделей

Нелинейные модели Линейные модели двух типов:- линейные по переменным- линейные по параметрамПримеры.1. Линейная модель множественной регрессии: Является линейной как по переменным, так и по параметрам2. Производственная функция Кобба-Дугласа: Является нелинейной как по переменным, так и параметру а1

Основные типы нелинейных моделей 1.Обобщенная модель нелинейная по переменным 2. Степенные функции 3. Показательные функции

Обобщенная модель нелинейная по переменным Линеаризация обобщенной нелинейной модели1. Вводятся новые переменные: 2. Подставляя новые переменные в модель (1), получим модель линейную по переменным z: 3. После оценки параметров модели делается обратный переход к модели (1.1)

Обобщенная модель нелинейная по переменным Примеры.1. Полиномиальные модели: Новые переменные: После перехода к новым переменным получается линейная модель множественной регрессии: Оценка и анализ проводится уже известными методами

Обобщенная модель нелинейная по переменным Полиномиальные модели:Параболические модели широко применяются- при моделировании средних и предельных издержек в зависимости от объема выпуска продукции- при моделировании зависимости прибыли предприятия от расходов на рекламуКубические модели – при моделировании общих издержек в зависимости от объема выпуска продукции

Обобщенная модель нелинейная по переменным 2. Модели гиперболического типа Новая переменная: В результате подстановки получим уравнение парной регрессии в виде:

Обобщенная модель нелинейная по переменным Модели параболического вида нашли применение при моделировании:- зависимости спроса от цен- зависимости спроса от дохода (кривые Энгеля)- спрос на предметы роскоши от дохода (функции Торнквиста)- уровня относительного изменения заработной платы в зависимости от относительного изменения уровня безработицы (кривая Филлипса)

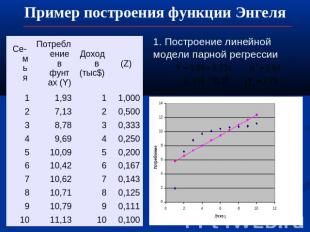
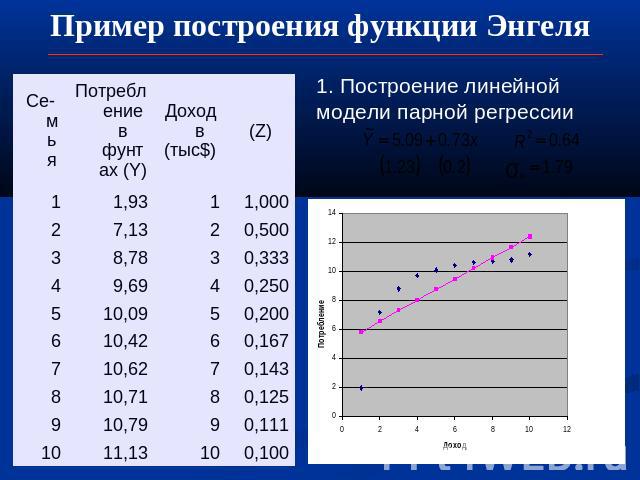
Пример построения функции Энгеля 1. Построение линейной модели парной регрессии

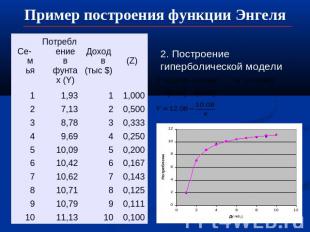
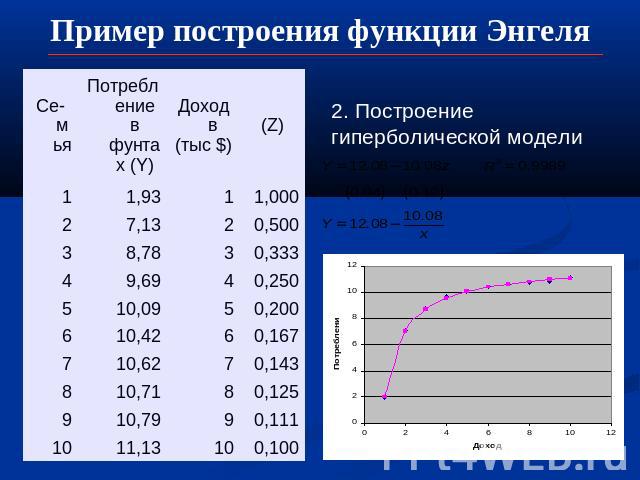
Пример построения функции Энгеля 2. Построение гиперболической модели

Пример построения функции Энгеля Меняется экономический смысл параметров модели:Линейная модель а0 – минимально необходимое потребление, а1 – предельное потребление- Гиперболическая модель: а0 – максимальное потребление, а1 – экономической интерпретации не имеет Предельное потребление равно:Эластичность:

Пример временного ряда 3. Временные ряды (динамические модели)Например вида: где f(t) – функция временного трендаT – период внутри которого производится моделирование

Степенные модели Степенная модель нелинейна по параметрам 1. Метод линеаризации – логарифмирование с последующим введением новых переменных: 2. Вводятся новые переменные и параметры: В новых переменных исходное уравнение принимает вид уравнения множественной регрессии:

Степенные модели 3. Оцениваются параметры b0, b1, b2 – методом наименьших квадратов и проверяются гипотезы о выполнении предпосылок теоремы Гаусса-Маркова для модели (2.3)4. Осуществляется возврат к исходной модели (2.1): В частном случае, когда в модели присутствует одна экзогенная переменная модель называют двойной логарифмической

Экономическая интерпретация параметров двойной логарифмической модели Двойная логарифмическая модель: Дифференцируем (2.4) по х Откуда получаем, что: Параметр а1 имеет смысл эластичности переменной Y по переменной x

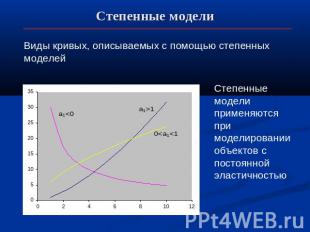
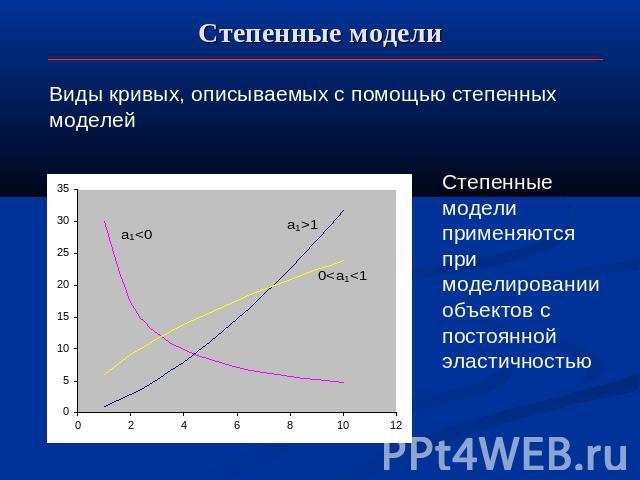
Степенные модели Виды кривых, описываемых с помощью степенных моделей Степенные модели применяются при моделировании объектов с постоянной эластичностью

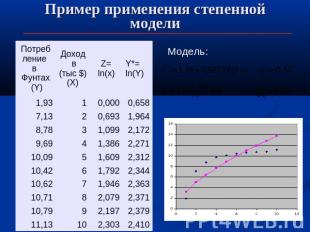
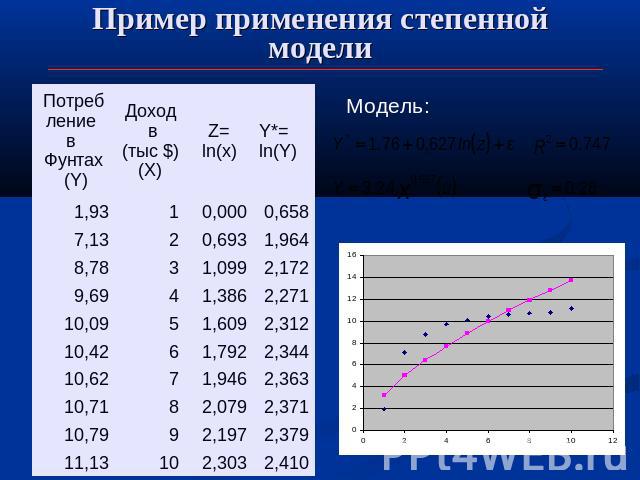
Пример применения степенной модели

Показательные функции в моделях Показательная (экспоненциальная) Модель 1. Метод линеаризации - логарифмирование 2. Введение новых переменных и параметров: 3. Оценка линейной регрессионной модели 4. Обратный переход к исходной модели (3.1)

Показательные функции в моделях Экономическая интерпретация коэффициентов моделиДифференцируем уравнение (3.1) по Х Экономический смысл коэффициента а1 в модели (3.1) – темп роста переменной YКоэффициент а0 – начальное значение переменной YПоказательные функции находят применение при моделировании процессов с постоянным темпом роста

Полулогарифмические модели Экспоненциальную модель (3.1) в виде (3.2) называют также полулогарифмической.К полуэкспоненциальным относят также модель вида: С помощью моделей вида (3.3) описывают процессы, обладающие свойством насыщения. Например, кривые Энгеля для товаров повседневного спроса.

Кинематические функции Перла-Рида Вид функции: 1. Способ линеаризации - логарифмирование 2. Вод новых переменных 3. Переход к модели множественной регрессии в новых переменных

Сложная экспоненциальная модель Общий вид модели Линеаризация в два этапв:1. Логарфмирование После введения переменной Y*=ln(Y), получится модель типа (1.1)