Презентация на тему: Приложение производной в школьном курсе математики

тема урока:Приложение производной в школьном курсе математики

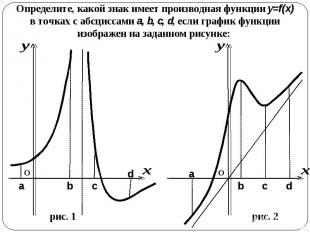
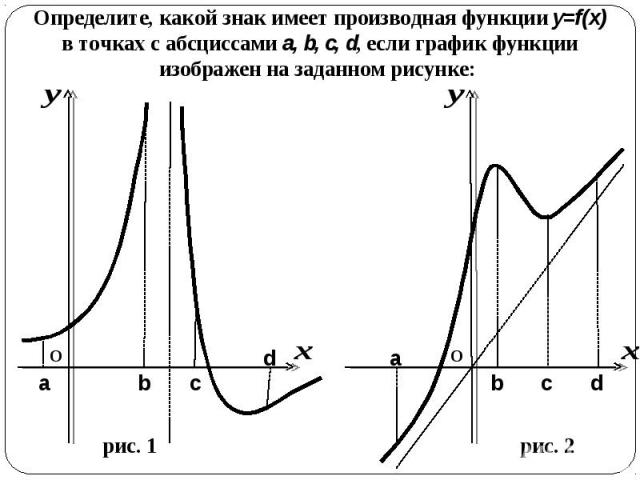
Определите, какой знак имеет производная функции y=f(x) в точках с абсциссами a, b, c, d, если график функции изображен на заданном рисунке:

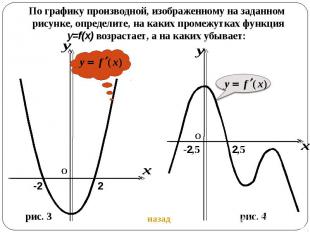
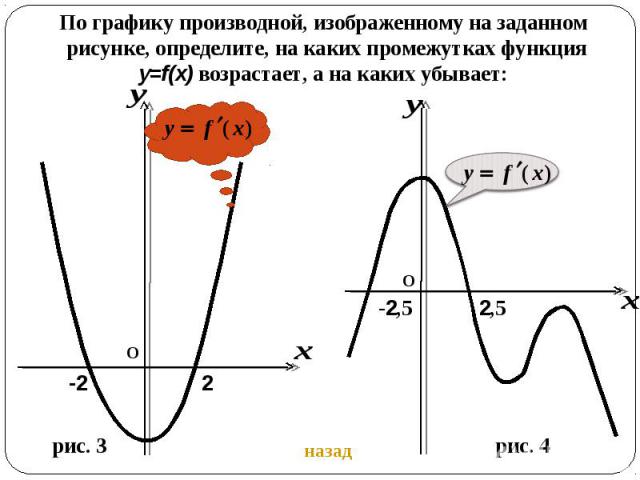
По графику производной, изображенному на заданном рисунке, определите, на каких промежутках функция y=f(x) возрастает, а на каких убывает:

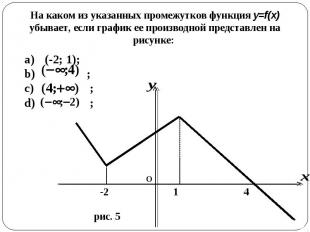
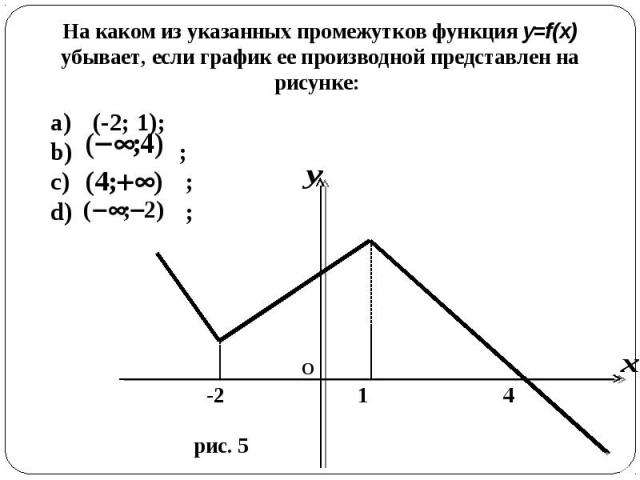
На каком из указанных промежутков функция y=f(x) убывает, если график ее производной представлен на рисунке:

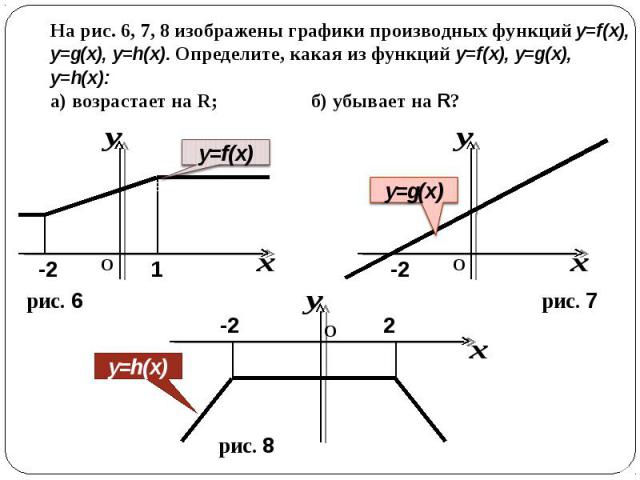
На рис. 6, 7, 8 изображены графики производных функций y=f(x), y=g(x), y=h(x). Определите, какая из функций y=f(x), y=g(x), y=h(x):а) возрастает на R; б) убывает на R?

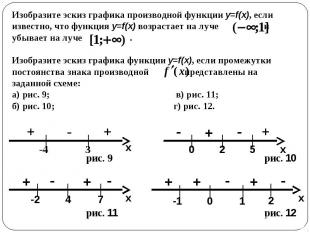
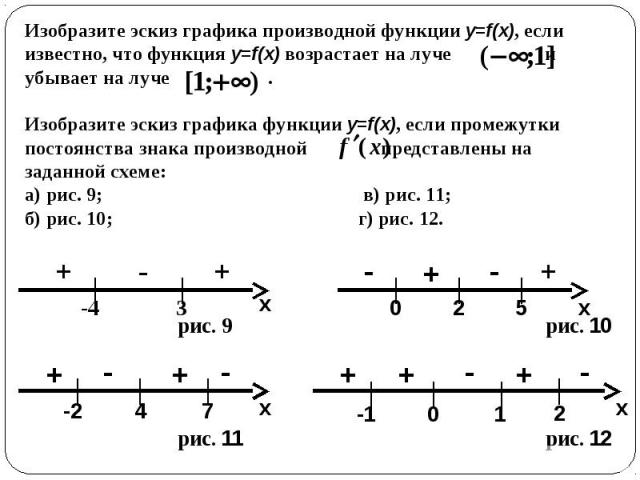
Изобразите эскиз графика производной функции y=f(x), если известно, что функция y=f(x) возрастает на луче и убывает на луче . Изобразите эскиз графика функции y=f(x), если промежутки постоянства знака производной представлены на заданной схеме: а) рис. 9; в) рис. 11; б) рис. 10; г) рис. 12.

Докажите, что функция монотонна на всей числовой прямой; укажите характер монотонности: а) , б) Исследуйте на монотонность функцию y=f(x) и постройте (схематически) ее график: .

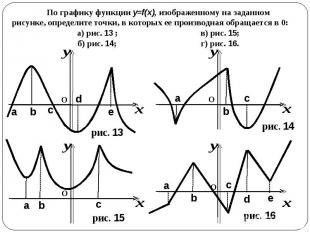
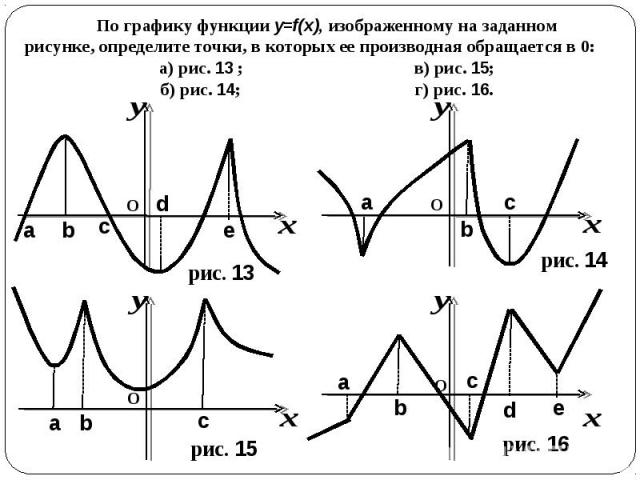
По графику функции y=f(x), изображенному на заданном рисунке, определите точки, в которых ее производная обращается в 0: а) рис. 13 ; в) рис. 15; б) рис. 14; г) рис. 16.

По графику функции y=f(x), изображенному на заданном рисунке, определите точки, в которых не существует производной: а) рис. 13; в) рис. 15; б) рис. 14; г) рис. 16. Сколько точек минимума имеет функция y=f(x), график которой изображен на заданном рисунке: а) рис. 13; в) рис. 15; б) рис. 14; г) рис. 16? Сколько точек максимума имеет функция y=f(x), график которой изображен на заданном рисунке: а) рис. 13; в) рис. 15; б) рис. 14; г) рис. 16? По графику производной, изображенному на заданном рисунке, определите, имеет ли функция y=f(x) точки экстремума: а) рис. 3; в) рис. 4;

Найдите стационарные и критические точки функции:а) , в) , б) , г) . Найдите точки экстремума заданной функции и определите их характер: а) , в) , б) , г) .

Спасибо за внимание!