Презентация на тему: Практическое применение производной

Практическое применение производной(Решение задач с межпредметным содержанием)Автор: Соболева Е.К.

ЦЕЛЬ УРОКА повторить, обобщить, систематизировать знания по данной теме ; показать учащимся необходимость знания материала изученной темы при решении прикладных задач; обратить внимание на связь данной темы с физикой и другими науками сформировать начальное представление об истории развития математического анализа. способствовать формированию умений применять приемы: сравнения , обобщения, выделения главного, перенос знаний в новую ситуацию,; развитию математического кругозора, мышления, математической речи, внимания и памяти.содействовать воспитанию интереса к математике и ее приложениям, развивать культуру общения, активность; способствовать развитию творческой деятельности учащихся.

ПЛАН УРОКАI. Организационный момент.II. Проверка домашнего задания и постановка проблемы.III. Обобщение и систематизация знаний.IV. Самопроверка знаний.V. Решение прикладных задач.VI. Подведение итогов.VII. Домашнее задание.

ЭПИГРАФ К УРОКУ« Лишь дифференциальное исчисление дает естествознанию возможность изображать математически не только состояния, но и процессы: движение » Ф. Энгельс«… Нет ни одной области в математике, которая когда – либо не окажется применимой к явлениям действительного мира …» Н.И. Лобачевский

Проверка домашнего задания1. Что называется математическим анализом?Ответ: это раздел математики, в котором изучается дифференциальное и интегральное исчисление 3. Докажите, что появление новой теории связано с развитием общества и его практическими потребностями.Ответ: в 15 – 17 веках в Европе назревала техническая революция. Шло преобразование производства на базе изобретения паровых машин, то есть необходимо было решать проблемы практической деятельности в гидротехнике, мореплавании, военном деле.

Проверка домашнего задания4. Кто и в каком году ввел термин «производная»?Ответ: Луи Лагранж в 1791 году5. В чем состоит механический смысл производной?Ответ: v(t)=s’(t); a(t)=v’(t), где s(t)- путь, пройденный телом за время t, v(t)- скорость тела в момент времени t; a(t) – ускорение тела в момент времени t

Повторение материала 1. Подберите функцию, производная которой равна: А) х2+4; Б) х6 ; В) 4х2 – 2; Г) sinx + 1/cos2x 2. Какие данные пропущены в таблице?

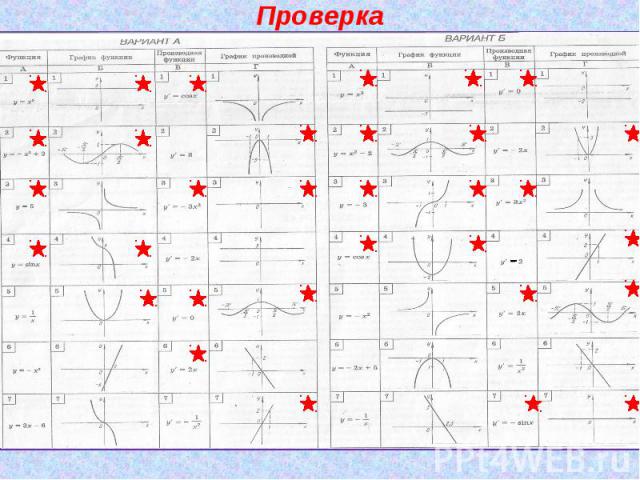
Повторение материала3. Установите соответствия между функцией, записанной в столбце А, ее графиком, изображенным в столбце Б, производной функции в столбце В и графиком производной в столбце Г. Например, из варианта А: 1А – 5Б – 6В – 7Г.

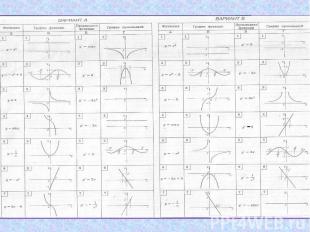
ПроверкаЗадание.Ответы: а) f(x)=x3/3+4x; б) f(x)=x7/7; в) f(x)=x4-2x; г) f(x)=-cosx+tgx2. Задание.Ответы : А) (xsinx)’=x’sinx+x(sinx)’=sinx+xcosx; Б) (sinx+xcosx)’=cosx+x’cosx+x(cosx)’=cosx+cosx-xsinx =2cosx-xsinx.

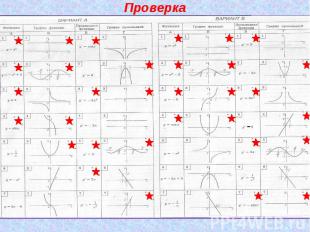
Проверка

Практическое применение1. Тело движется прямолинейно по закону s(t)=3+2t+t2 (м). Определите его скорость и ускорение в момент времени t=3с.2. Тело массой 0,5 кг движется прямолинейно по закону s(t)=2t2–2t–3 (м). Найдите кинетическую энергию тала через 3 с. после начала движения, а также значение силы F, действующей на тело.3. Известно, что для любой точки стержня АВ длиной 10 см масса куска стержня АС длиной p определяется по формуле m(n)=4n2+3n. Найдите линейную плотность стержня в середине отрезка.

Практическое применение4. Количество электричества, прошедшее через проводник начиная с момента t = 0, задается формулой q(t)=2t2+3t+1. Найдите силу тока в конце пятой секунды.5. Количество тепла Q необходимого для нагревания 1 кг воды от00С до t 0С, определяется по формуле Q(t)=t+0,00002t2+0,0000003t3. Вычислите теплоемкость воды для t=1000С . Теплоемкость тела есть производная от количества тепла по температуре.

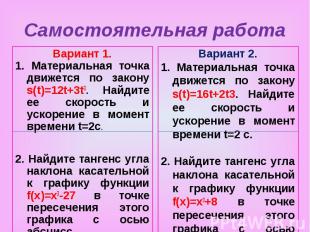
Самостоятельная работаВариант 1.1. Материальная точка движется по закону s(t)=12t+3t3. Найдите ее скорость и ускорение в момент времени t=2с.2. Найдите тангенс угла наклона касательной к графику функции f(x)=x3-27 в точке пересечения этого графика с осью абсцисс.Вариант 2.1. Материальная точка движется по закону s(t)=16t+2t3. Найдите ее скорость и ускорение в момент времени t=2 с.2. Найдите тангенс угла наклона касательной к графику функции f(x)=x3+8 в точке пересечения этого графика с осью абсцисс.

СамопроверкаВариант 1.v(t)=s’(t)= 12+9t²; v(2)=12+36= 48 (м/с); a(t)=v’(t)= 18t; a(2)=18·2= 36 (м/с²).2. f(x)= 0; x³-27= 0; x³= 27; x= 3, т.е. х0= 3. f’(x)=3x²; f’(x0)= f’(3)=27 Значит, tgx= 27.Вариант 2.v(t)=s’(t)= 16+6t²; v(2)= 40 (м/с); a(t)=v’(t)= 12t; a(2)= 24 (м/с²).2. х0 = -2; так как при пересечении с осью абсцисс f(x)= 0. f’(x)=3x²; f’(x0)= f’(-2)=12 Значит, tgx= 12.

Домашнее заданиеПодготовить п.21 из учебника.Решить задачи №271, 272.Дополнительное задание: Найти и подготовить решение трех задач по теме «Практическое применение производной». Сделать презентацию подобранных задач.