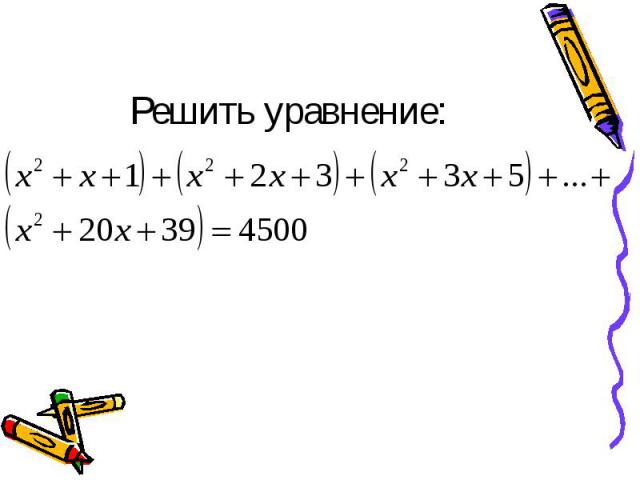Презентация на тему: Прогрессии

Нестандартные задачи по теме «Прогрессии» Цель урока: расширить и углубить знания по теме «Прогрессии»

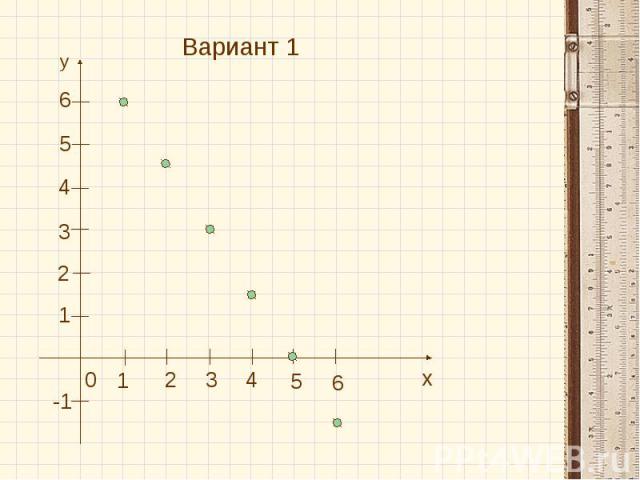
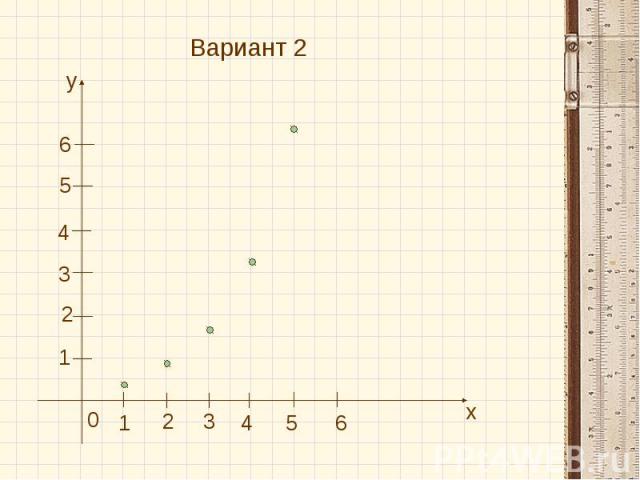
Лабораторно-графическая работа Вариант 1Построить график арифметической прогрессии(аn), у которой аз=3, а4=1,5, 1≤n≤6. Вариант 2Докажите, что последовательность bn=0,2·2n является геометрической прогрессией. Постройте график этой последовательности для 1≤n≤5.

Вариант 1

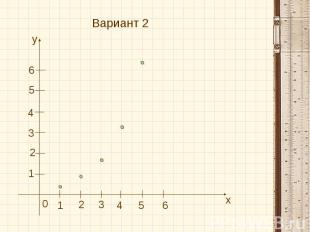
Вариант 2

Устная задача Журнал состоит из 16 вложенных в друг друга двойных листов. На каком двойном листе сумма чисел, обозначающих номера страниц будет наибольшей.

Сведения из истории Абу-р-Райхан-аль Бируни (973-1048) Леонардо из Пизы (1170-1228)

Задача Докажите, что числа вида где n N, не образуют арифметическую прогрессию.

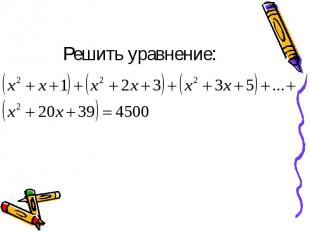
Решить уравнение:

Устная управляемая самостоятельная работа 1) а14 = 41; а12 = -1; а13 - ? (k1) 2) a5=12; a3=k1; a7 - ? (k2)3) a1+a20=k2; a3+a18 - ? (k3)4) b2=k3; b1b3 - ? (k4)5) b3=9; b5=k4; b7- ? (k5)6) b3b7=k5; b2b8 - ?Ответы для самоконтроля: 9; 4; 16; 20; 4; 9.

Задача Положительные числа а1, а2, а3, … аn образуют арифметическую прогрессию. Докажите, что