Презентация на тему: Прогрессии

Арифметическая и геометрическая прогрессии

Цели и задачи урока Цели урока: Образовательные: обобщение и систематизация теоретических знаний учащихся по изученной теме; подготовка к ГИА; Развивающие: развитие математического мышления учащихся и вычислительных навыков. Воспитательные: содействовать воспитанию интереса к математике и её приложениям. Тип урока: урок повторения, обобщения и систематизации знаний. Оборудование: компьютер, мультимедийный проектор, экран, карточки.

Арифметическая и геометрическая прогрессии Арифметическая и геометрическая прогрессии

Лист самооценки За каждый правильный ответ при опросе и за участие на различных этапах урока ставьте один плюс. «5» - более 9 плюсов «4» - от 5 до 8 плюсов менее 5 плюсов – оценку не заработал

Эпиграф урока «Дороги не те знания, которые откладываются в мозгу, как жир, дороги те, которые превращаются в умственные мышцы». (Герберт Спенсер, английский философ)

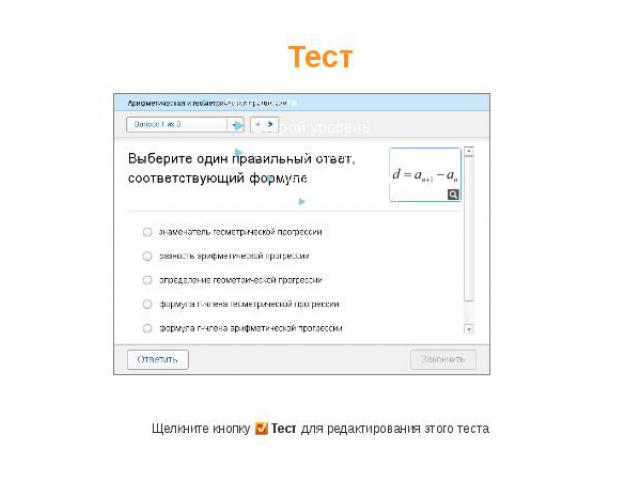
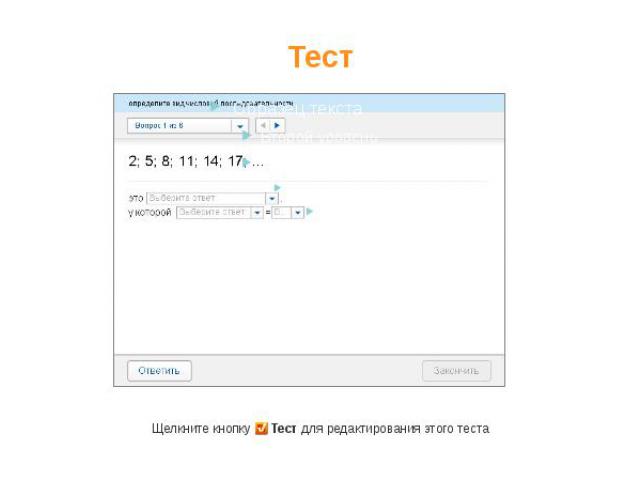
Тестирование


Устная работа

Назад, в историю! На связь между прогрессиями первым обратил внимание великий АРХИМЕД (ок. 287–212 гг. до н.э.) Термин «прогрессия» был введён римским автором Боэцием (в 6 веке) и понимался в более широком смысле, как бесконечная числовая последовательность. В переводе с латинского, слово progressio означает «движение вперёд». Названия «арифметическая» и «геометрическая» были перенесены из теории непрерывных пропорций, которыми занимались древние греки. Формула суммы членов арифметической прогрессии была доказана древнегреческим учёным Диофантом (в 3 веке). Формула суммы членов геометрической прогрессии дана в книге Евклида «Начала» (3 век до н.э.). Правило для нахождения суммы членов произвольной арифметической прогрессии впервые встречается в сочинении «Книги абака» в 1202г. (Леонардо Пизанский) А общее правило для суммирования любой конечной геометрической прогрессии встречается в книге Никола Шюке «Наука о числах», увидевшей свет в 1484 году.

Работа у доски

Физкультминутка

Цитата часа

Характерное свойство арифметической прогрессии используя свойство

Характерное свойство геометрической прогрессии используя свойство


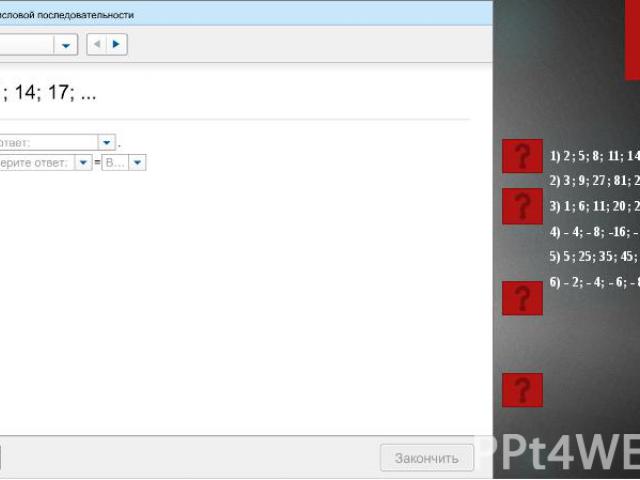
Самостоятельная работа 1) Дано: (аn), а1 = - 3, а2 = 4. Найти: а16 – ? 2) Дано: (bn), b12 = - 32, b13 = - 16. Найти: q – ? 3) Дано: (аn), а21 = - 44, а22 = - 42. Найти: d – ? 4) Дано: (bn), bп > 0, b2 = 4, b4 = 9. Найти: b3 – ? 5) Дано: (аn), а1 = 28, а21 = 4. Найти: d – ? 6) Дано: (bn), b1=1/2, q = 2. Найти: b5 – ? 7) Дано: (аn), а7 = 16, а9 = 30. Найти: а8 – ?


Интересные факты 1) Химия. При повышении температуры по арифметической прогрессии скорость химических реакций растёт по геометрической прогрессии. 2) Геометрия. Вписанные друг в друга правильные треугольники образуют геометрическую прогрессию. 3) Физика. И в физических процессах встречается эта закономерность. Нейтрон, ударяя по ядру урана, раскалывает его на две части. Получаются два нейтрона. Затем два нейтрона, ударяя по двум ядрам, раскалывает их ещё на 4 части и т.д. – это геометрическая прогрессия. 4) Биология. Микроорганизмы размножаются делением пополам, поэтому при благоприятных условиях, через одинаковый промежуток времени их число удваивается. 5) Экономика. Вклады в банках увеличиваются по схемам сложных и простых процентов. Простые проценты – увеличение первоначального вклада в арифметической прогрессии, сложные проценты – увеличение в геометрической прогрессии.

Домашнее задание из сборника ГИА 6.1. 1) Пятый член арифметической прогрессии равен 8,4 , а её десятый член равен 14,4. Найдите пятнадцатый член этой прогрессии. 6.2. 1) Число -3,8 является восьмым членом арифметической прогрессии (ап), а число -11 является её двенадцатым членом. Является ли членом этой прогрессии число -30,8 ? 6.5. 1) Между числами 6 и 17 вставьте четыре числа так, чтобы вместе с данными числами они образовали арифметическую прогрессию. 6.8. 1) В геометрической прогрессии b12 = З15 и b14 = З17. Найдите b1.

Рефлексивный экран

Урок сегодня завершён, Урок сегодня завершён, Но каждый должен знать: Познание, упорство, труд К прогрессу в жизни приведут!

Спасибо за урок! Спасибо за урок!

Используемые источники и ПО Алгебра. 9 класс : учеб. Для общеобразоват. учреждений / [Макарычев Ю.Н., Миндюк Г.Н., Нешков К.И., Суворова С.Б.] ; под ред. Теляковского С.А. – 16-е изд. – М. : Просвещение, 2009. – 271 с. : ил. Канина Г. В., учитель математики. Урок-презентация «Арифметическая и геометрическая прогрессия» [Электронный ресурс] – URL: http://festival.1september.ru/articles/534291/ (27.02.2013). Мелом пишут по доске [Звук] – URL: http://zvuki-tut.narod.ru/melom_pishut_po_doske/Melom_pishut_po_doske.mp3 (28.02.2012). Пойа Д. [Картинка] – URL: http://www.apm.pt/pic/_polya_5252dffc9e0eb.jpg (28.02.2013). Спенсер Г. [Картинка] – URL: http://upload.wikimedia.org/wikipedia/commons/thumb/9/96/Herbert_Spencer.jpg/389px-Herbert_Spencer.jpg (28.02.2013). Шалкина С. В., учитель математики. Здоровьесберегающие технологии на уроках математики [Электронный ресурс] – URL: http://festival.1september.ru/articles/311946/ (01.03.2013). iSpring Presenter 7 - разработка тестов и преобразование во flash. MS PowerPoint 2010 - разработка презентации.

Работа у доски. Задание 1 используя формулу а n = а1 + d . (n 1)

Работа у доски. Задание 2 используя формулу bn = b1 q n-1

Работа у доски. Задание 3 используя формулу а n = а1 + d . (n 1)
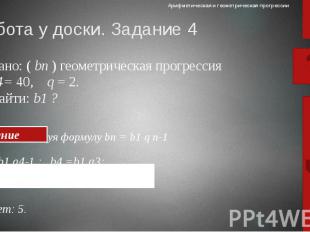
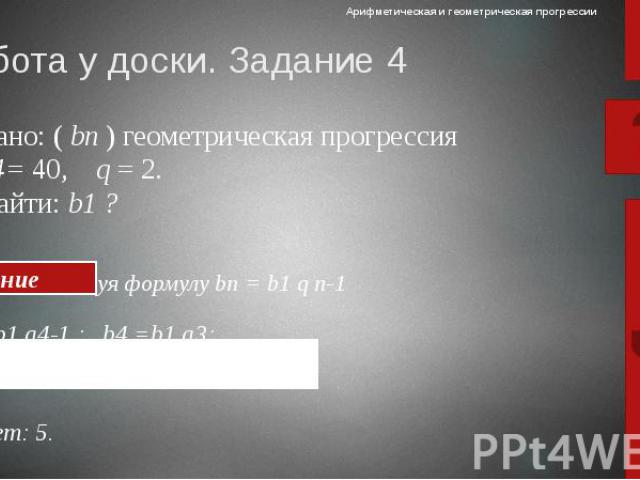
Работа у доски. Задание 4 используя формулу bn = b1 q n-1

Определение арифм. прогр.

Свойство арифм. прогр.

Определение геометр. прогр.

Свойство геометр. прогр.

Гимнастика для глаз, вверх-вниз

Гимнастика для глаз, влево-вправо

Гимнастика для глаз, диагональ
Гимнастика для глаз, овал

Гимнастика для глаз, восьмёрка

Гимнастика для глаз, моргание

Гимнастика для тела
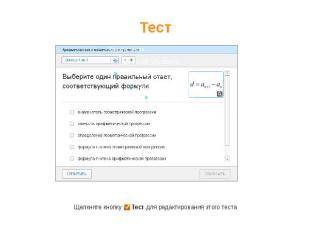
`
























![Используемые источники и ПО Алгебра. 9 класс : учеб. Для общеобразоват. учреждений / [Макарычев Ю.Н., Миндюк Г.Н., Нешков К.И., Суворова С.Б.] ; под ред. Теляковского С.А. – 16-е изд. – М. : Просвещение, 2009. – 271 с. : ил. Канина Г. В., учитель ма… Используемые источники и ПО Алгебра. 9 класс : учеб. Для общеобразоват. учреждений / [Макарычев Ю.Н., Миндюк Г.Н., Нешков К.И., Суворова С.Б.] ; под ред. Теляковского С.А. – 16-е изд. – М. : Просвещение, 2009. – 271 с. : ил. Канина Г. В., учитель ма…](https://fs1.ppt4web.ru/images/95245/112761/640/img23.jpg)