Презентация на тему: Арифметическая и геометрическая прогрессии

Закончился двадцатый век. Куда стремится человек? Изучены космос и море, Строенье звезд и вся Земля. Но математиков зовет Известный лозунг: «Прогрессио- движение вперед».


Арифметическая и геометрическая прогрессии обобщение и систематизация теоретического материала по данной теме; отработка умений и навыков применения формул n –го члена прогрессии, суммы n первых членов прогрессии; развитие навыков работы с дополнительной литературой, с историческим материалом; развитие познавательной активности учащихся; воспитание эстетических качеств и умения общаться; формирование интереса к математике.

ИСТОРИЧЕСКАЯ СПРАВКА В клинописных таблицах вавилонян в египетских пирамидах(второй век до н.в.) встречаются примеры арифметический прогрессий. Задачи на прогрессии, дошедшие до нас из древности, были связаны с запросами хозяйственной жизни: распределение продуктов, деление наследства и др. Некоторые формулы, относящиеся к прогрессиям, были известны китайским и индийским ученым. Ариабхатта (5 в.)применял формулы общего числа, суммы арифметической прогрессии. Но правило для нахождения суммы членов арифметической прогрессии впервые встречается в сочинении «Книги Абака» в 1202 г.(Леонардо Пизанский).

Установи соответствие

Прогрессии Последовательность в которой каждый член начиная со второго равен предыдущему сложенному с одним и тем же числом. Последовательность отличных от нуля чисел в которой каждый член начиная со второго равен предыдущему умноженному на одно и тоже число.

Формула n-го члена прогрессии арифметической, геометрической

Характеристическое свойство прогрессий Арифметическая прогрессия Каждый член последовательности начиная со второго есть среднее арифметическое между предыдущим и последующим членами прогрессии Геометрическая прогрессия Каждый член последовательности начиная со второго есть среднее геометрическое между предыдущим и последующим членами последовательности (bn >0)

Формулы суммы n первых членов прогрессий
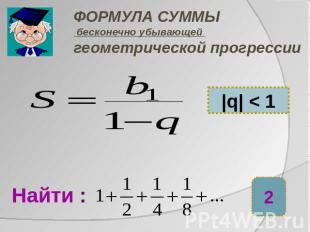
ФОРМУЛА СУММЫ бесконечно убывающей геометрической прогрессии

Самостоятельная работа ( тест) 1. Про арифметическую прогрессию (аn) известно, что а7 = 8, а8 = 12. найдите разность арифметической прогрессии. 2. Геометрическая прогрессия задана формулой 3. Члены арифметической прогрессии изображены (рис.1) точками на коорди-натной плоскости. Какое из данных чисел является членом этой прогрессии? 4. Найдите сумму семи первых членов геометрической прогрессии 4; 8; …

5. Последовательность аn задана формулой Найдите номер члена последовательности, равного 7. 6. В геометрической прогрессии (bn) b1 = 8, b3 = 24. Найдите b5. ( для q > 0 ) 7. Сумма второго и пятого членов арифметической прогрессии равна 11. Третий её член на 6 больше первого. Найдите второй и четвёртый члены.

Прогрессии в жизни, в быту и не только За 16 дней Карл украл у Клары 472 коралла. Каждый день он крал на 3 коралла больше, чем в предыдущий день. Сколько кораллов украл Карл в последний день. В сборнике по подготовке к экзамену-240 задач. Ученик планирует начать их решение 2 мая, а закончить 16 мая, решая каждый день на две задачи больше, чем в предыдущий день. Сколько задач ученик запланировал решить 12 мая? В амфитеатре расположены 10 рядов, причем в каждом следующем ряду на 20 мест больше чем в предыдущем, а в последнем ряду 280 мест. Сколько человек вмещает амфитеатр?

Считать несчастным тот день или тот час, в который ты не усвоил ничего нового, ничего не прибавил к своему образованию. Ян Амос Коменский Оцените свои знания и умения на конец урока. Был ли полезен урок для каждого из вас? Чем?

I (слайд 2 ) Тему сегодняшнего урока мы узнаем, разгадав кроссворд: 1. Как называется график квадратичной функции? 2. Математическое предложение, справедливость которого доказывается. 3. Упорядоченная пара чисел, задающая положение точки на плоскости. 4. Наука, возникшая в глубокой древности в Вавилоне и Египте, а учащиеся России начинают её изучать с 7 класса. 5. Линия на плоскости, задаваемая уравнением у=кх+b. 6. Числовой промежуток. 7. Предложение, принимаемое без доказательства. 8. Результат сложения 9. Название второй координаты на плоскости. 10. Французский математик 19 века, «отец» алгебры, юрист, разгадал шифр, применяемый испанцами в войне с французами, а нам помог в быстром решении квадратных уравнений. II (слайд 3) Итак, тема урока «Прогрессии». Прогрессия – латинское слово, означающее "движение вперед", было введено римским автором Боэцием. - А почему во множественном числе? Какие знаете прогрессии?Давайте сформулируем цели нашего урока.

V (слайды 11,12 ) самостоятельная работа (тест с проверкой ) VI (слайд 13 ) решение практических задач 3.Решение: 280= а₁ + 20∙(10-1); а₁= 280 - 20 ∙ 9 = 100; S₁₀ = ½(100+280) ∙ 10 =1900. Ответ:1900 человек вмещает амфитеатр. 1.Решение: S₁₆=½ (2∙а₁ + 3∙15) ∙16; 472 =16 а₁ + 360; а₁ = (472- 360):16=7. а₁₆ =7+ 3 ∙ (16-1)=52. Ответ: 52 коралла украл Карл в последний день. 2.Решение:240=½(2 а₁ +2 ∙14) ∙ 15; 240:15= а₁ + 14; а₁ = 2; а₁₁ = 2+2 ∙ 10 = 22. Ответ:22 задачи надо решить 12 мая.