Презентация на тему: Логические операции

Логические операции Логическое отрицание (инверсия)Логическое умножение (конъюнкция)Логическое сложение (дизъюнкция)Логическое следование (импликация)Логическое равенство (эквивалентность)

Логическая операция — способ построения сложного высказывания из данных высказываний, при котором значение истинности сложного высказывания полностью определяется значениями истинности исходных высказываний.Истинное высказывание в логике обозначается - 1, ложное – 0Высказывания обозначаются буквами латинского алфавита: А, В, С и т.д.

Логическое отрицание (инверсия) - образуется из высказывания с помощью добавления частицы «не» к сказуемому или использования оборота речи «неверно, что…».Обозначение инверсии:НЕ А;¬ A;Ā;NOT А. А = Дождя не будетĀ = Неверно, что дождя не будет. (Дождь будет. )

Истинность высказывания, имеющего форму Ā (вне зависимости от его содержания), определяется по специальной таблице истинности. Таблица истинности инверсии (неА): Логическое отрицание (инверсия) делает истинное высказывание ложным и, наоборот, ложное — истинным.

Графическая иллюстрация инверсии с помощью диаграмм Эйлера — Венна:А — множество отличников;Ā — множество неотличников.

Логическое умножение (конъюнкция) - образуется соединением двух высказываний в одно с помощью союза «и».Обозначение конъюнкции:A И B;A ۸ B;A & B;A B;A AND B.А = «10 делится на 2»В = «10 делится на 5» , A ۸ B = «10 делится на 2 и на 5».

Таблица истинности конъюнкции: Конъюнкция двух высказываний истинна тогда и только тогда, когда оба высказывания истинны, и ложна, когда хотя бы одно высказывание ложно.

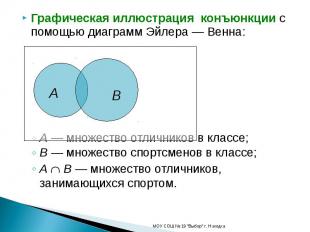
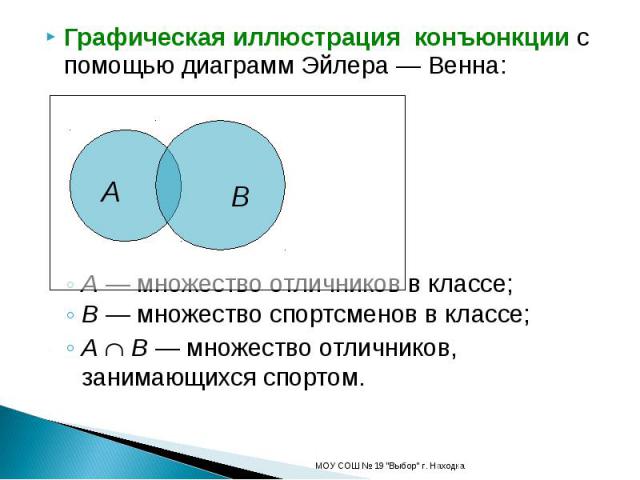
Графическая иллюстрация конъюнкции с помощью диаграмм Эйлера — Венна:A — множество отличников в классе;B — множество спортсменов в классе;A B — множество отличников, занимающихся спортом.

Логическое сложение (дизъюнкция) образуется соединением двух высказываний в одно с помощью союза «или».Союз «или» может использоваться:в неисключающем (объединительном) смысле — операция называется нестрогой дизъюнкцией;в исключающем (разделительном) смысле — операция называется строгой дизъюнкцией.

Примеры строгих и нестрогих дизъюнкций:

Под дизъюнкцией будем понимать нестрогую дизъюнкцию, если не оговорено иное.Обозначение дизъюнкции:A ИЛИ B;A OR B;A B;A ۷ B;A + B.

Таблица истинности дизъюнкции: Дизъюнкция двух высказываний ложна тогда и только тогда, когда оба высказывания ложны, и истинна, когда хотя бы одно высказывание истинно.

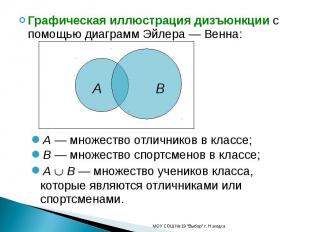
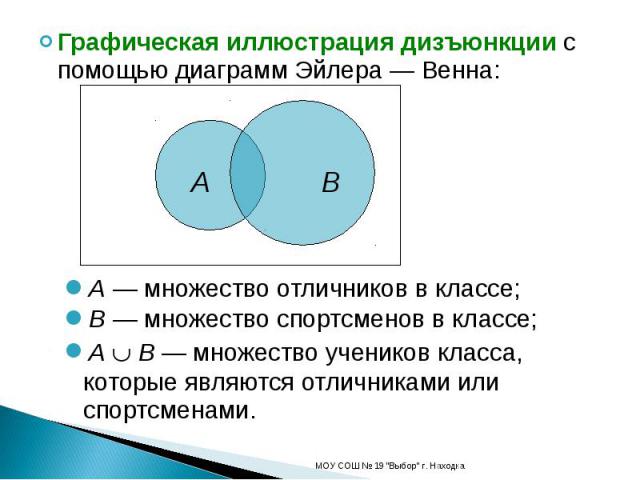
Графическая иллюстрация дизъюнкции с помощью диаграмм Эйлера — Венна:A — множество отличников в классе;B — множество спортсменов в классе;A B — множество учеников класса, которые являются отличниками или спортсменами.

Логическое следование (импликация) образуется соединением двух высказываний в одно с помощью оборота речи «если..., то...».E = Если клятва дана, то она должна выполняться.P = Если число делится на 9, то оно делится на 3.Обозначение импликации:A B;A B.

Таблица истинности импликации: Импликация двух высказываний ложна тогда и только тогда, когда из истинного высказывания следует ложное (Из истины не может следовать ложь).

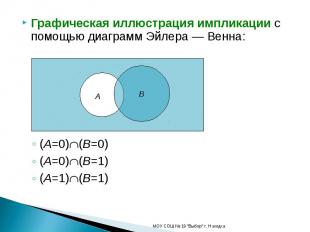
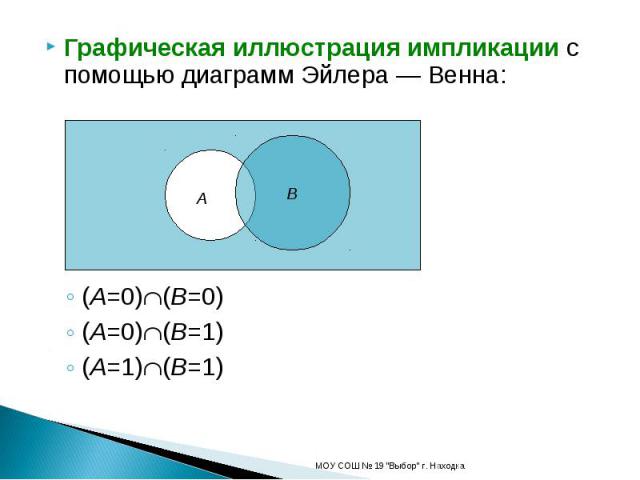
Графическая иллюстрация импликации с помощью диаграмм Эйлера — Венна:(A=0)(B=0)(A=0)(B=1)(A=1)(B=1)

Логическое равенство (эквивалентность) образуется соединением двух высказываний в одно при помощи оборота речи «…тогда и только тогда, когда...».Угол называется прямым тогда и только тогда, когда он равен 90°.Голова думает тогда и только тогда, когда язык отдыхает.Обозначение эквивалентности:A B;A B;A ~ B.

Таблица истинности эквивалентности: Эквивалентность двух высказываний истинна или когда оба высказывания истинны или когда оба ложны.

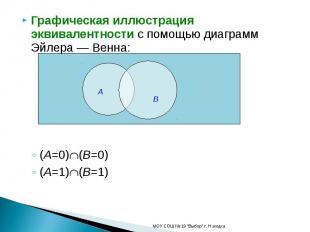
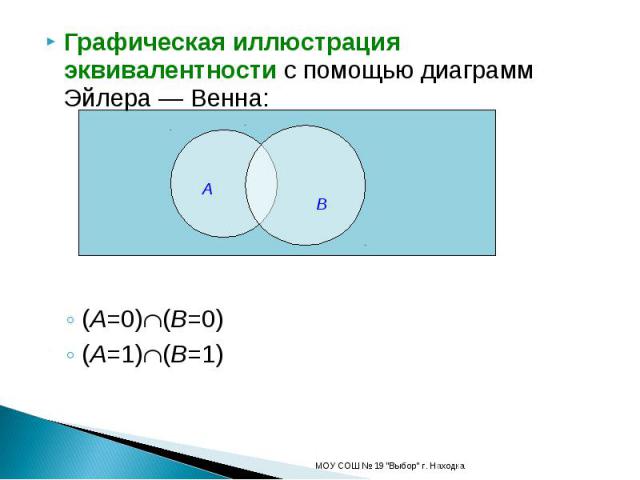
Графическая иллюстрация эквивалентности с помощью диаграмм Эйлера — Венна:(A=0)(B=0)(A=1)(B=1)

Литература Лыскова В.Ю., Ракитина Е.А. Логика в информатике.Семакин И.Г., Вараксин Г.С. Информатика. Структурированный конспект базового курса.Под ред. Семакина И.Г. Информатика. Задачник-практикум в 2 т. Том 1.Шауцукова Л.З. Информатика: Учебное пособие для 10-11 классов общеобразовательных учреждений.Угринович Н.Д. Информатика и информационные технологии. Учебник для 10-11 классов.