Презентация на тему: Числа Фибоначчи и золотое сечение

Числа Фибоначчи и золотое сечение МБОУ «Малыгинская средняя общеобразовательная школа» Выполнила ученица 9 «а» классаКузнецова Юлияпод руководствомучителя математикиБольшаковой О.К.

«Числа не управляют миром, но показывают, как управляется мир»

Труды:«Книга Абака»«Книга квадратов»«Практика геометрии»………… Леонардо Пизанский(Фибоначчи)1170-1240 1.Введение десятичной системы исчисления в Европе.2.Приобщение Европейских ученых к достижениям индийских и арабских математиков

«Сколько пар кроликов родится в течении года, если известно, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца после своего рождения"

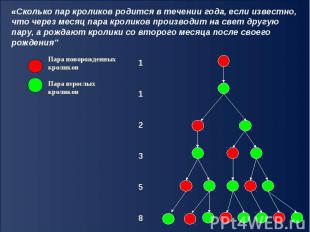
«Сколько пар кроликов родится в течении года, если известно, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца после своего рождения" Пара новорожденных кроликов

Числа Фибоначчи:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610,…1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610,…1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610,…1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610,…1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610,…

Числа Фибоначчи1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610,… Свойства последовательности : Каждое третье число Фибоначчи четноКаждое четвертое делится на триКаждое пятнадцатое оканчивается нулемДва соседних числа взаимно просты

Числа Фибоначчи:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610,… Коэффициент Фибоначчи: φ(фи)=0,618…(Золотой коэффициент, золотая середина) 1:1=1,0000 1:2=0,5000 2:3=0,666 3:5=0,6000 5:8=0,6250 8:13=0,6150 13:21=0,6190 21:34=0,6170 34:55=0,6180 55:89=0,6179 Фидий (v в. до н.э.) (древнегреческий скульптор)

Определение Золотого сечения Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всемуa:b=b:c или с:b=b:а.

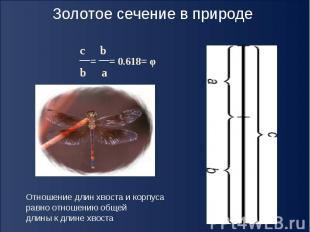
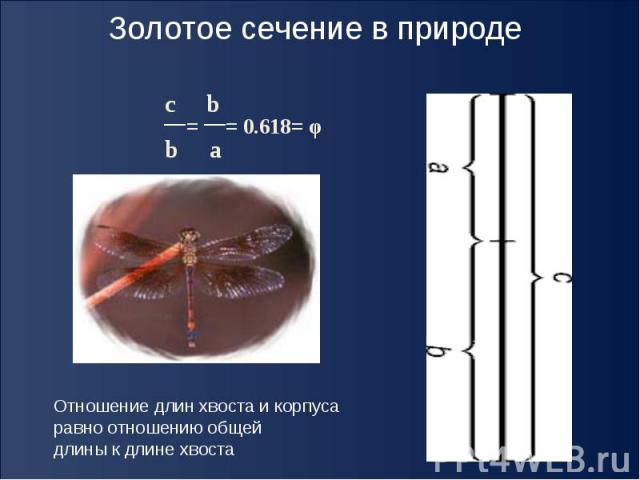
Золотое сечение в природе Отношение длин хвоста и корпусаравно отношению общей длины к длине хвоста

Числа Фибоначчи проявляются в строенииразличных организмов 5, 8, 13, 21, 34, 55…

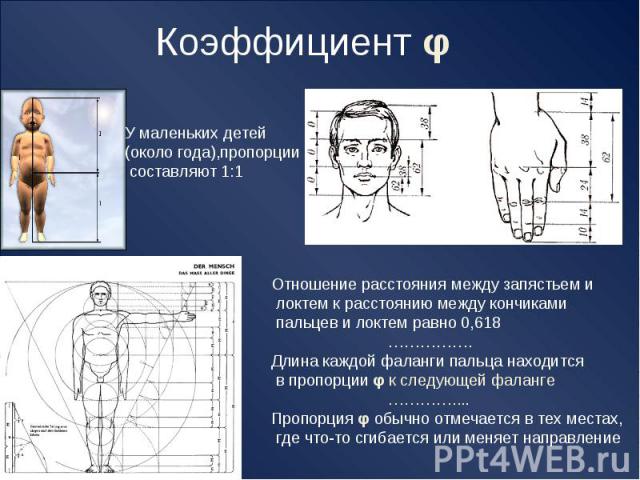
Коэффициент φ У маленьких детей (около года),пропорции составляют 1:1 Отношение расстояния между запястьем и локтем к расстоянию между кончиками пальцев и локтем равно 0,618 …………….Длина каждой фаланги пальца находится в пропорции φ к следующей фаланге …………....Пропорция φ обычно отмечается в тех местах, где что-то сгибается или меняет направление

Числа Фибоначчи в природе сельдерей (1 и 2) Ананас(8 и 13) сосновая шишка (5 и 8)

Числа Фибоначчи в природе Семена в подсолнухе растут по спиралям одновременно по и против часовой стрелки от центра цветка наружу. Кол-во спиралей по и против часовой стрелки – это два соседних числа Фибоначчи (34 и 55)

Числа Фибоначчи в природе. Попав во время каникул куда-нибудь на юг или в ботанический сад, незабудьте изучить разные сочные плоды и кактусы! Попробуйте поискать растения , в которых встречается пара 2 и 3; 3 и 5; 5 и 8; 13 и 21.Может быть они найдутся в вашем саду…

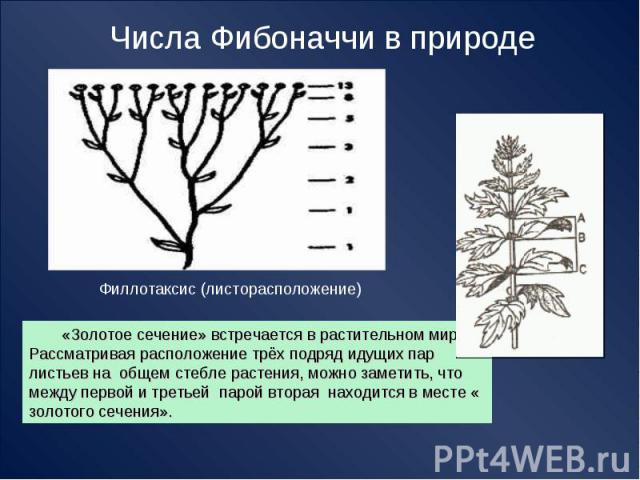
Числа Фибоначчи в природе Филлотаксис (листорасположение) «Золотое сечение» встречается в растительном мире. Рассматривая расположение трёх подряд идущих пар листьев на общем стебле растения, можно заметить, что между первой и третьей парой вторая находится в месте « золотого сечения».

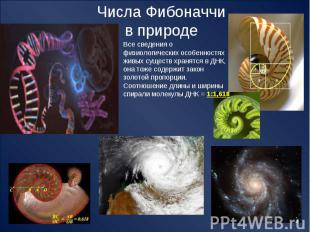
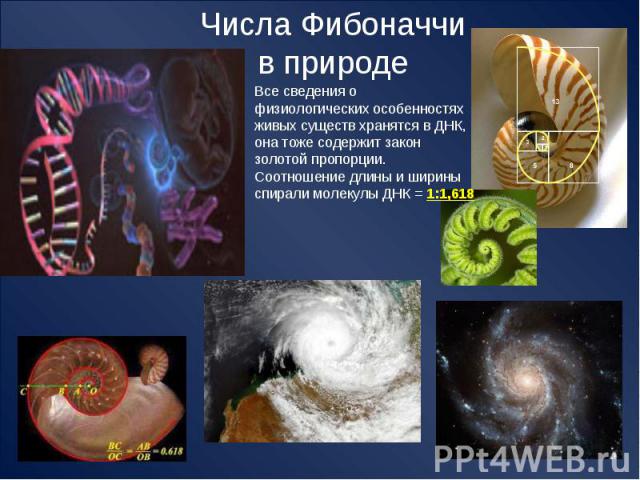
Числа Фибоначчив природе Все сведения о физиологических особенностях живых существ хранятся в ДНК, она тоже содержит закон золотой пропорции. Соотношение длины и ширины спирали молекулы ДНК = 1:1,618

Проявление Золотого сечения в искусстве. Замечательный пример «золотого сечения» представляет собой правильный пятиугольник - выпуклый и звездчатый.Звездчатый пятиугольник называется пентаграммой. Пифагорейцы выбрали пятиконечную звезду в качестве талисмана , она считалась символом здоровья.

«Джоконда» Портрет Моны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника.

На знаменитой картине И.И.Шишкина «Сосновая роща» с очевидностью просматриваются мотивы золотого сечения. Ярко освещенная солнцем сосна (стоящая на первом плане) делит длину картины по золотому сечению. Справа от сосны – освещённый солнцем пригорок. Он делит по золотому сечению правую часть картины по горизонтали. Слева от главной сосны находится множество сосен - при желании можно с успехом продолжить деление картины по золотому сечению и дальше. «Сосновая роща»

Проявление Золотого сечения в архитектуре Пирамида Хеопса Длина грани, деленная на высоту, приводит к соотношению φ=0,618

Парфенон Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным. Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по золотому сечению, то получим те или иные выступы фасада.

Храм Василия Блаженного Пропорции Покровского собора на Красной площади в Москве определяются восемью числами Фибоначчи. Многие числа здесь повторяются в затейливых элементах храма многократно.

Проявление золотого сечения в музыке В качестве примера построения скрипки на основе закона Золотого сечения возьмем скрипку работы Антонио Страдивари, созданную им в 1700 году.

Проявление золотого сечения в скульптуре Великий древнегреческий скульптор Фидий часто использовал «золотое сечение» в своих произведениях. Самыми знаменитыми из них были статуя ЗевсаОлимпийского (которая считалась одним из чудес света) и Афины Парфенос.

Хотя Фибоначчи был одним из величайших математиков, единственные памятники ему- это статуя напротив Пизанской башни и две улицы, одна – в Пизе, а другая во Флоренции. Кажется странным, что так мало людей, приходящих к Пизанской башне, когда - либо слышали о Фибоначчи или обращали внимание на памятник ему.

На Земле, как и во всей Вселенной, дают о себе знать удивительный порядок и совершенная гармония. Зачастую их невозможно выразить словами и тогда приходится обращаться к языку математики (языку чисел). Вот почему так важно изучать и его. В природе действительно существует основной закон пропорции и коэффициент Фибоначчи помогает понять его. Красота и математика неразрывно связаны друг с другом.