Презентация на тему: Правильные многогранники

Правильные многогранники Выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число рёбер.

Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук. Л. Кэрролл

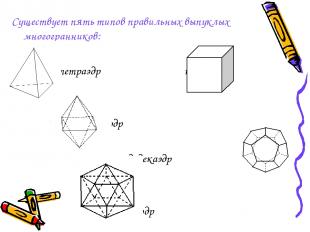
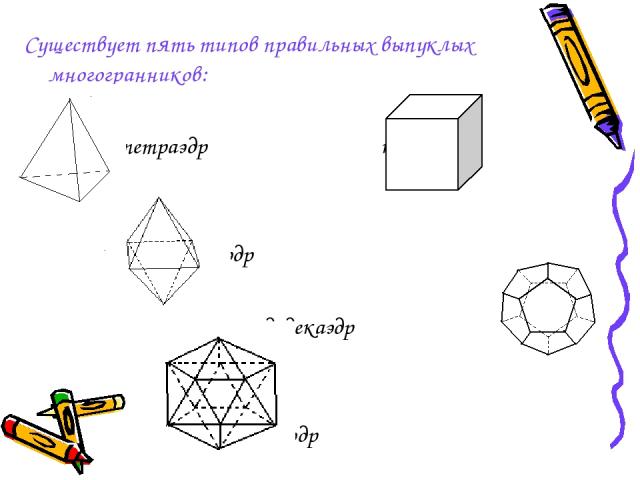
Существует пять типов правильных выпуклых многогранников: тетраэдр куб октаэдр додекаэдр икосаэдр

Названия многогранников пришли из Древней Греции, в них указывается число граней: «эдра» грань; «тетра» 4; «гекса» 6; «окта» 8; «икоса» 20; «додека» 12.

Правильные многогранники иногда называют Платоновыми телами, поскольку они занимают видное место в философской картине мира, разработанной великим мыслителем Древней Греции Платоном (ок. 428 – ок. 348 до н.э.). Платон считал, что мир строится из четырёх «стихий» – огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников. Правильные многогранники в философской картине мира Платона

Тетраэдр - огонь Тетраэдр олицетворял огонь, поскольку его вершина устремлена вверх, как у разгоревшегося пламени.

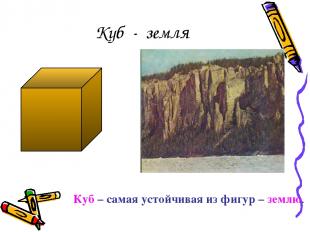
Куб - земля Куб – самая устойчивая из фигур – землю.

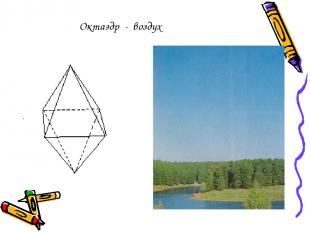
Октаэдр - воздух

Икосаэдр - вода Икосаэдр – как самый обтекаемый – воду

Додекаэдр - вселенная Пятый многогранник – додекаэдр символизировал весь мир и почитался главнейшим.

«Мой дом построен по законам самой строгой архитектуры. Сам Евклид мог бы поучиться, познавая геометрию моих сот.» (Из сказки «Тысяча и одна ночь»

Правильные многогранники встречаются в живой природе. Например, скелет одноклеточного организма феодарии (Circjgjnia icosahtdra) по форме напоминает икосаэдр. Чем же вызвана такая природная геометризация феодарий? По-видимому, тем, что из всех многогранников с тем же числом граней именно икосаэдр имеет наибольший объём при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление водной толщи. Правильные многогранники – самые «выгодные» фигуры. И природа этим широко пользуется. Подтверждением тому служит форма некоторых кристаллов.

Кристаллы некоторых известных нам веществ имеют форму правильных и полуправильных многогранников. Куб передает форму кристаллов поваренной соли, кристалл сернистого колчедана имеет форму додекаэдра, бор - икосаэдр

Кристаллы алмаза обычно имеют форму октаэдра

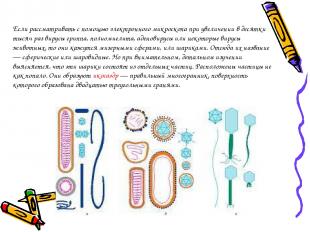
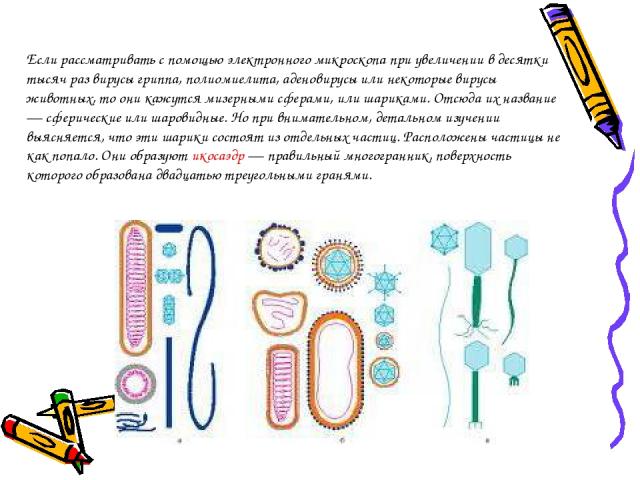
Если рассматривать с помощью электронного микроскопа при увеличении в десятки тысяч раз вирусы гриппа, полиомиелита, аденовирусы или некоторые вирусы животных, то они кажутся мизерными сферами, или шариками. Отсюда их название — сферические или шаровидные. Но при внимательном, детальном изучении выясняется, что эти шарики состоят из отдельных частиц. Расположены частицы не как попало. Они образуют икосаэдр — правильный многогранник, поверхность которого образована двадцатью треугольными гранями.

Почему эти вирусы имеют форму правильного многогранника, а именно икосаэдра? Оказывается, все дело в экономии. Допустим, вам дали треугольные кирпичики и сказали, чтобы вы из них самым экономным способом сложили замкнутую оболочку. Строгие законы точной науки — математики подскажут вам, что в данном случае следует сложить икосаэдр. Природа, как самый гениальный математик, придала телу вирусов форму икосаэдра. По-видимому, дело здесь не только в экономии строительного материала. Вирус в клетке должен совершить настоящий переворот, поработить ее и заставить работать на себя. Для этого он должен быть «умным». Он в миллионы раз меньше клетки. Весь план переворота нормальной жизни клетки должен быть тщательно записан, зашифрован в «мозгу» вируса — нуклеиновой кислоте. Поэтому «мозг» вируса должен быть как можно более объемистым, чтобы туда все уместилось. Но масса его ограничена. Для зашифровки тайны своей жизни в «мозгу» вируса оставлено совсем немного места. Таким способом достигается не только экономия строительного материала» но и -экономия генетической информации. Вирусы устроены не только просто, но и чрезвычайно целесообразно. Когда природа их лепила, она отбрасывала все ненужное, нерациональное.

Теорема Эйлера: Для всякого выпуклого многогранника между числами В, Г и Р выполняется соотношение В + Г – Р = 2 название Тетраэдр куб октаэдр додекэдр икосаэдр Число граней и их форма 4 6 8 12 20 Число вершин 4 8 6 20 12 Число ребер 6 12 12 30 30

Художник Альбрехт Дюрер Знаменитый художник, увлекавшийся геометрией, Альбрехт Дюрер (1471-1528гг.), в известной гравюре „Меланхолия” на переднем плане изобразил додекаэдр.

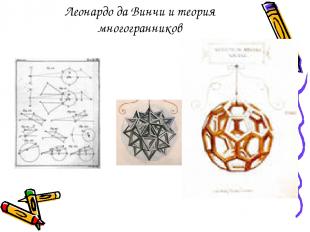
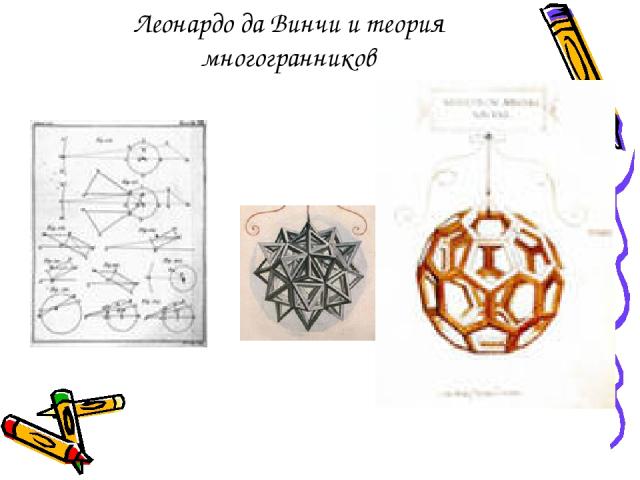
Леонардо да Винчи и теория многогранников

Сальвадор Дали Тайная вечеря

Мауриц Эшер

По версии В. Макарова и В. Морозова ядро Земли имеет форму и свойства растущего кристалла, оказывающего воздействие на развитие всех природных процессов. Лучи этого кристалла обуславливают икосаэдро-додекаэдровую структуру Земли. Она проявляется в том, что в земной коре как бы проступают проекции вписанных в земной шар правильных многогранников: икосаэдра и додекаэдра. Многие залежи полезных ископаемых тянутся вдоль икосаэдро-додекаэдровой сетки; 62 вершины и середины рёбер многогранников, называемых авторами узлами, обладают рядом специфических свойств, позволяющих объяснить некоторые непонятные явления. Здесь располагаются очаги древнейших культур и цивилизаций: Перу, Северная Монголия, Гаити, Обская культура и другие. В этих точках наблюдаются максимумы и минимумы атмосферного давления, гигантские завихрения Мирового океана. В этих узлах находятся озеро Лох-Несс, Бермудский треугольник. Икосаэдро-додекаэдрическая структура Земли