Презентация на тему: Решение заданий №23

Решение заданий № 23 Учитель математики МОУ СОШ № 25 с УИОП Радионова Е.Ю.

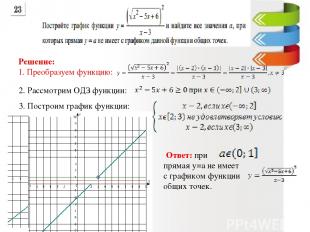
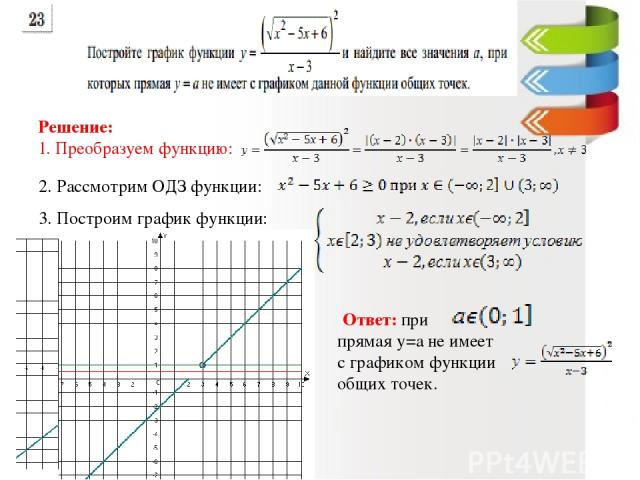
3. Построим график функции: Решение: 1. Преобразуем функцию: 2. Рассмотрим ОДЗ функции:

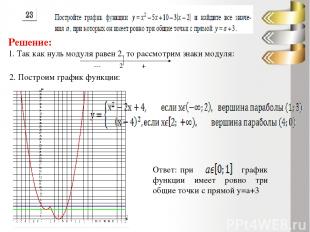
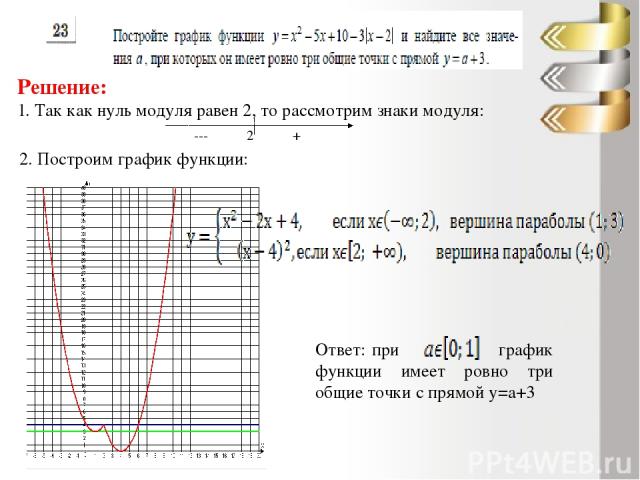
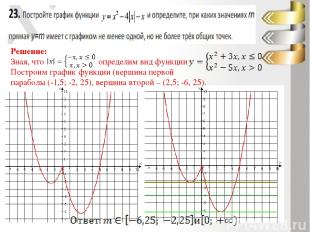
Решение: 1. Так как нуль модуля равен 2, то рассмотрим знаки модуля: 2. Построим график функции: Ответ: при график функции имеет ровно три общие точки с прямой у=а+3

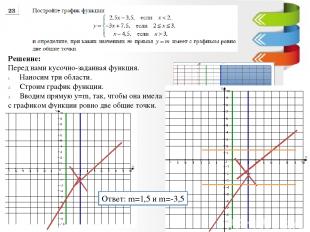
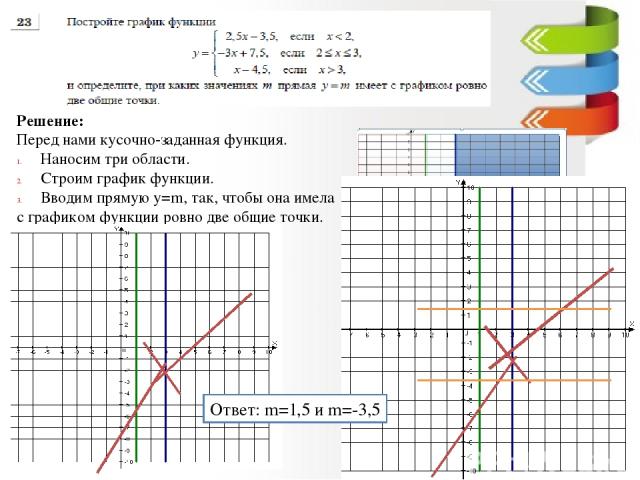
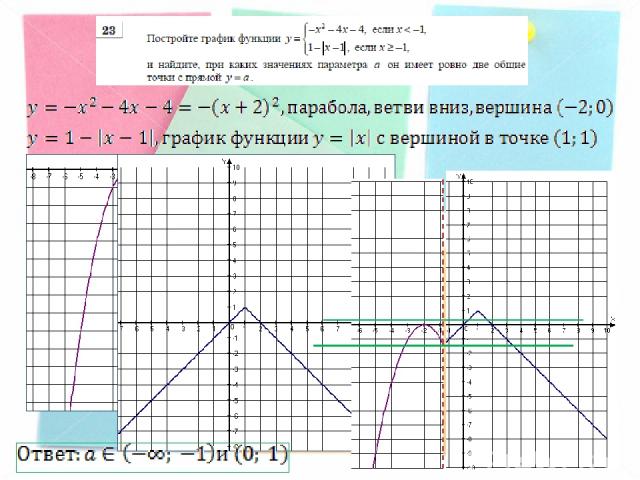
Решение: Перед нами кусочно-заданная функция. Наносим три области. Строим график функции. Вводим прямую у=m, так, чтобы она имела с графиком функции ровно две общие точки. Ответ: m=1,5 и m=-3,5

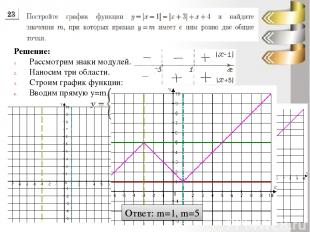
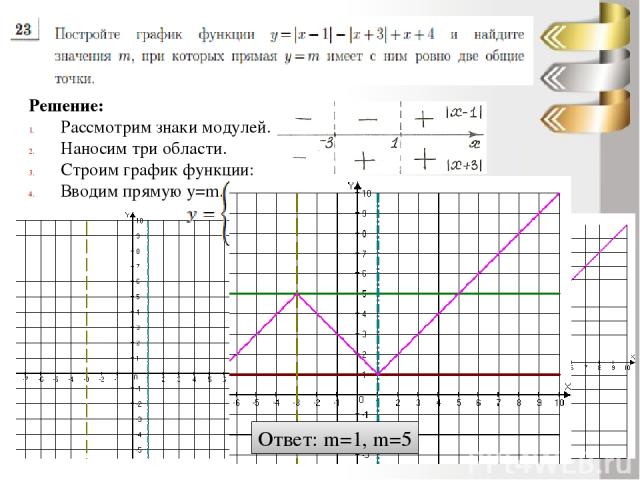
Решение: Рассмотрим знаки модулей. Наносим три области. Строим график функции: Вводим прямую y=m. Ответ: m=1, m=5

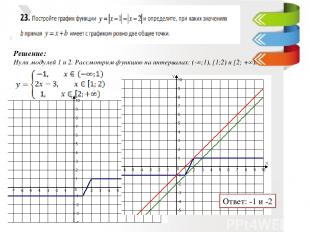
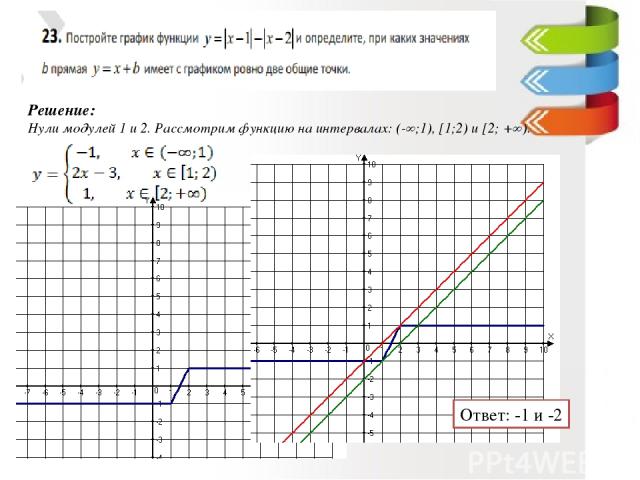
Ответ: -1 и -2 Решение: Нули модулей 1 и 2. Рассмотрим функцию на интервалах: (-∞;1), [1;2) и [2; +∞).

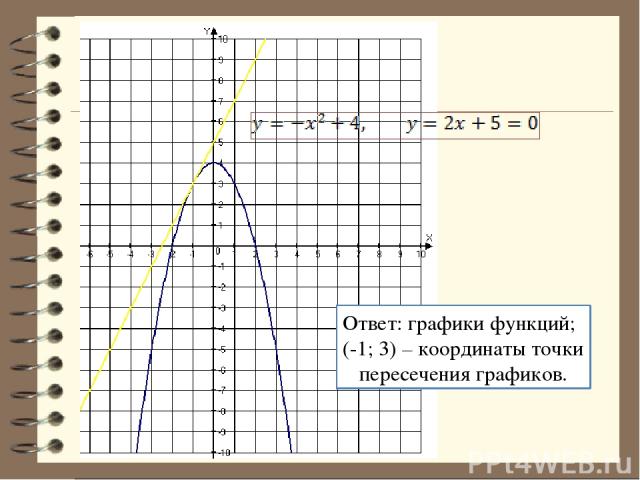
Решение: 1. Так как графики функций имеют общую точку, то приравняем правые части уравнений 2. Точка одна, значит квадратное уравнение имеет одно решение (D=0). Найдем дискриминант (4р -16=0, р=4). 3. Определим координаты этой точки: (-1; 3). 4. Построим в одной системе координат графики этих функций:

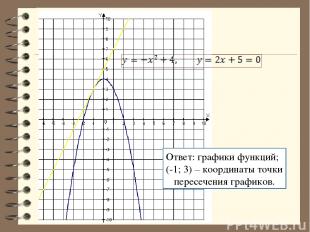
Ответ: графики функций; (-1; 3) – координаты точки пересечения графиков.

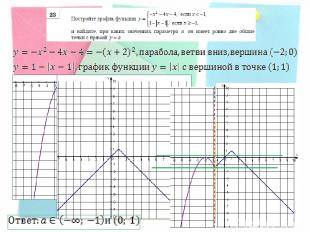
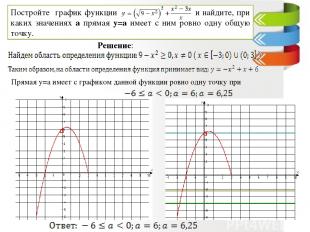
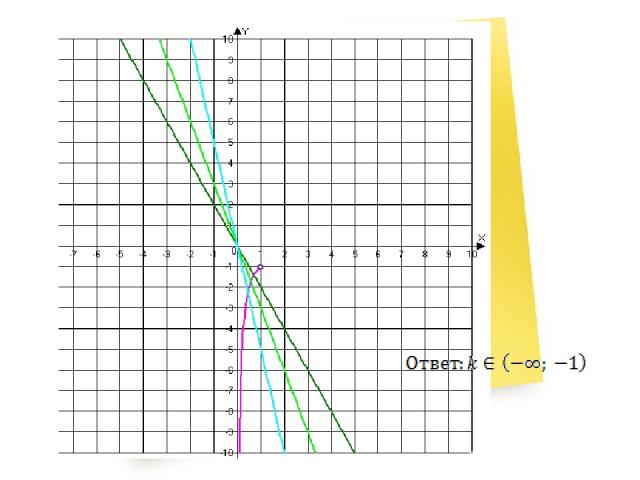
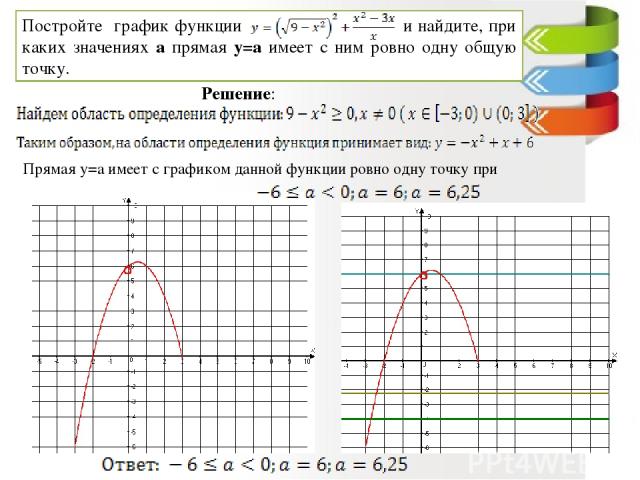
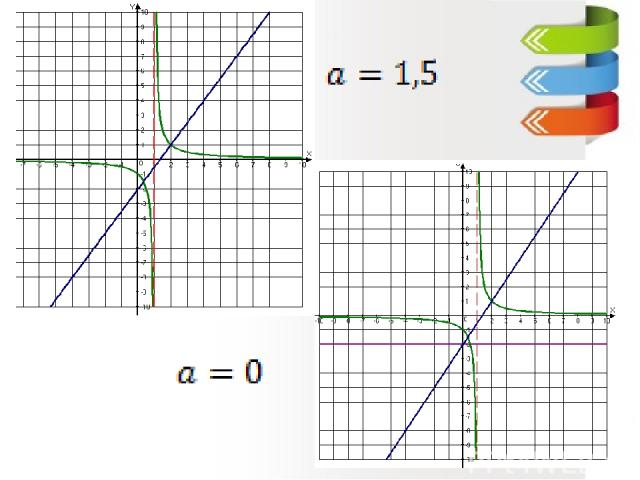
Прямая y=a имеет с графиком данной функции ровно одну точку при Решение: Постройте график функции и найдите, при каких значениях а прямая у=а имеет с ним ровно одну общую точку.

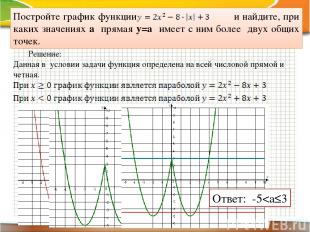
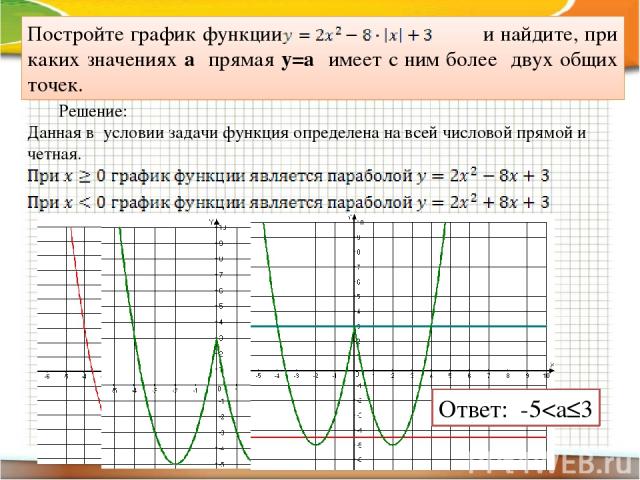
Постройте график функции и найдите, при каких значениях а прямая у=а имеет с ним более двух общих точек. Решение: Данная в условии задачи функция определена на всей числовой прямой и четная. Ответ: -5

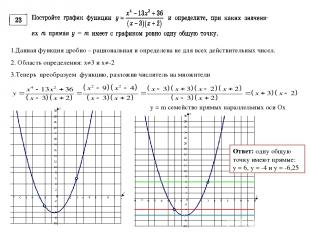
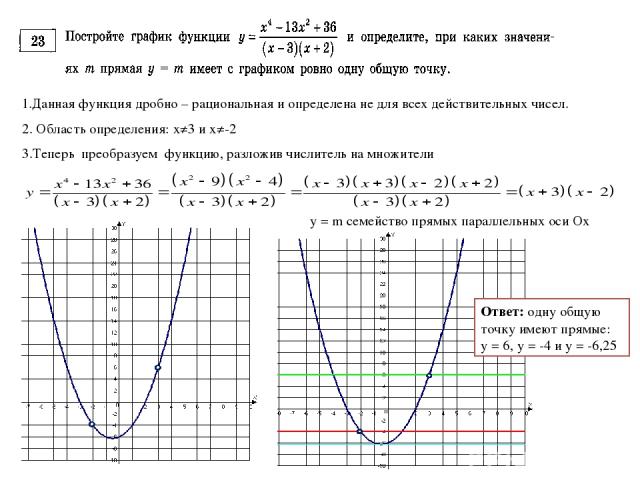
1.Данная функция дробно – рациональная и определена не для всех действительных чисел. 2. Область определения: x≠3 и x≠-2 3.Теперь преобразуем функцию, разложив числитель на множители y = m семейство прямых параллельных оси Ох Ответ: одну общую точку имеют прямые: у = 6, у = -4 и y = -6,25

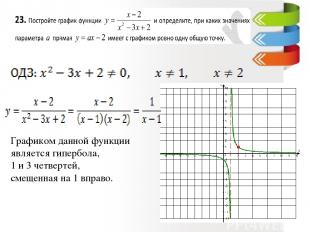
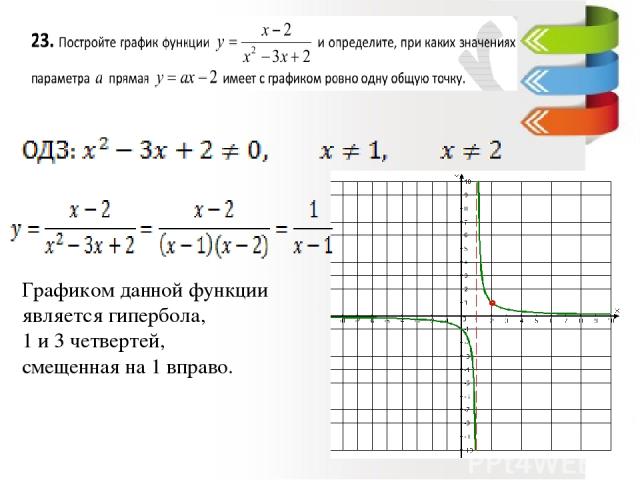
Графиком данной функции является гипербола, 1 и 3 четвертей, смещенная на 1 вправо.