Презентация на тему: Конус

Автор работы: Ахтарова Э. Л. 10 класс. Красноуфимск 2012 г Конус Сказала мама: «А сейчас про конус будет мой рассказ. В высокой шапке звездочет Считает звезды круглый год. КОНУС – шляпа звездочета. Вот какой он. Понял? То-то». ГБОУ СПО СО «КПК»

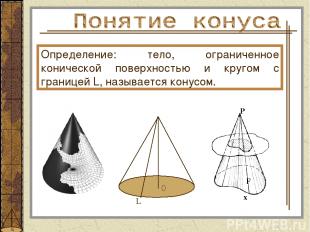
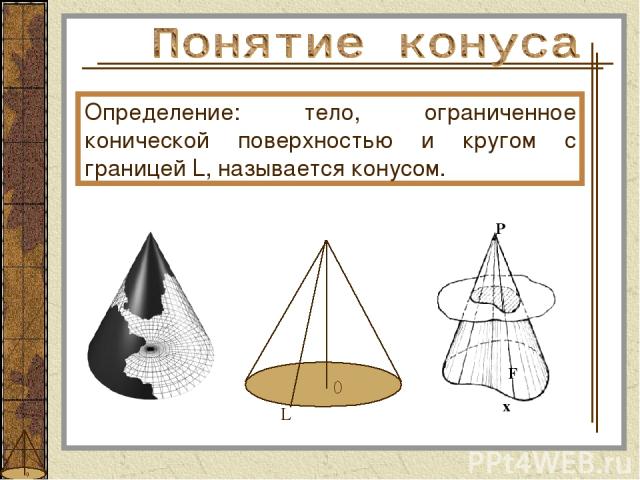
Определение: тело, ограниченное конической поверхностью и кругом с границей L, называется конусом.

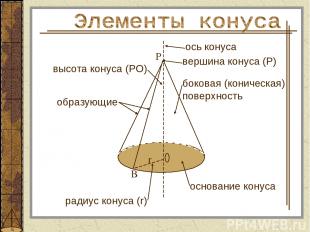
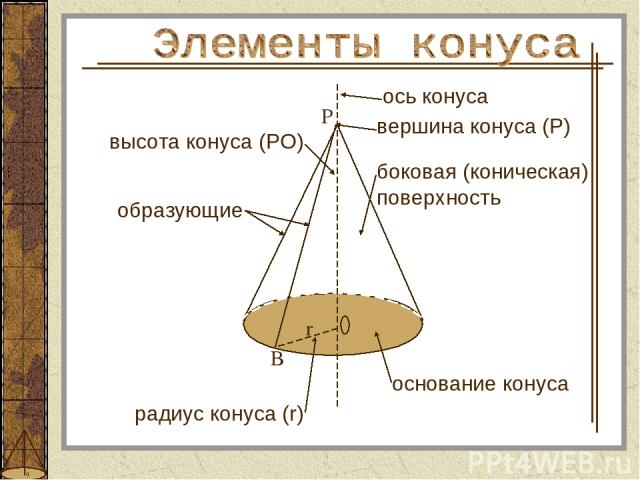
боковая (коническая) поверхность высота конуса (РО) ось конуса вершина конуса (Р) основание конуса радиус конуса (r) B r образующие P

Образующие - отрезки, соединяющие вершину конуса с точками окружности; Ось – прямая, содержащая его высоту; Высота – перпендикуляр, опущенный из вершины конуса на плоскость основания; Основание конуса – круг.

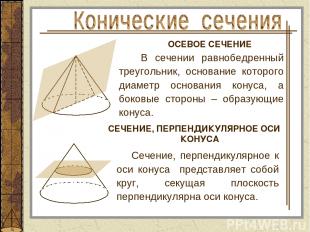
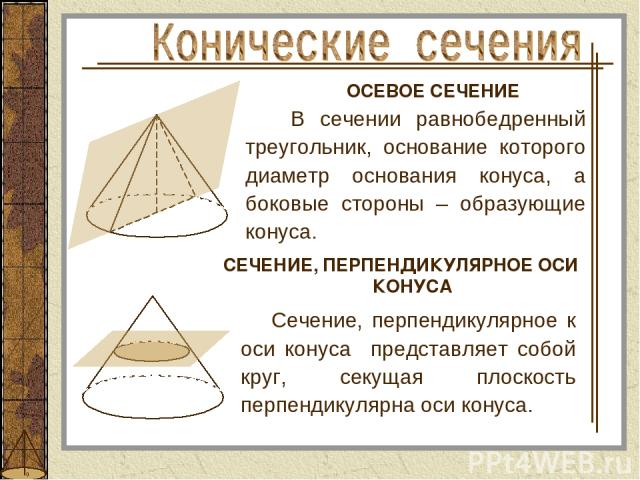
Сечение, перпендикулярное к оси конуса представляет собой круг, секущая плоскость перпендикулярна оси конуса. ОСЕВОЕ СЕЧЕНИЕ СЕЧЕНИЕ, ПЕРПЕНДИКУЛЯРНОЕ ОСИ КОНУСА В сечении равнобедренный треугольник, основание которого диаметр основания конуса, а боковые стороны – образующие конуса.

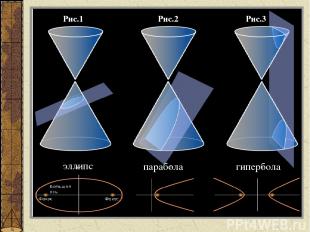
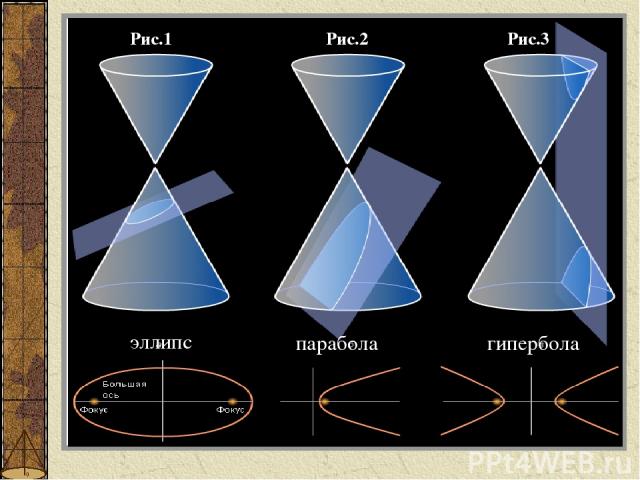
Рис.1 Рис.2 Рис.3 эллипс парабола гипербола

За площадь боковой поверхности конуса принимается площадь его развертки (конической поверхности). Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую. Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания.

Задача 1. Объем конуса равен 6см3. Чему равен объем цилиндра, который имеет такое же основание и такую же высоту, как и данный конус? Ответ: 18

Задача 2 Объем цилиндра равен 12см3. Чему равен объем конуса , который имеет такое же основание и такую же высоту, как и данный цилиндр? Ответ: 4 В меню

Задача 3 Радиус основания первого конуса в 2 раза меньше, чем радиус основания второго конуса, а образующая первого конуса в 3 раза больше, чем образующая второго. Чему равна площадь боковой поверхности первого конуса, если площадь боковой поверхности второго равна 22 см2? Ответ: 33 В меню

Задача 4 Радиус основания первого конуса в 3 раза меньше, чем радиус основания второго конуса, а образующая первого конуса в 2 раза больше, чем образующая второго. Чему равна площадь боковой поверхности первого конуса, если площадь боковой поверхности второго равна 18 см2? Ответ: 12 В меню

Задача 5 Объём конуса равен 18π дм3. Осевое сечение конуса – прямоугольный треугольник. Найти высоту.

Задача 6 Длина образующей конуса – 10 см, диаметр его основания - 12 см. Найти высоту конуса.

Конус в переводе с греческого «konos» означает «сосновая шишка». С конусом люди знакомы с глубокой древности. Много сделала для геометрии школа Платона (428–348 гг. до н. э.). Школе Платона, в частности, принадлежит: а) исследование свойств призмы, пирамиды, цилиндра и конуса; б) изучение конических сечений.

Большой трактат о конических сечениях был написан Аполлонием Пергским – учеником Евклида, который создал великий труд из 15 книг под названием «Начала». Эти книги издаются и по сей день, а в школах Англии по ним учатся до сих пор.

Перейти к домашнему заданию

Найти объем цилиндра, вписанного в конус с объемом 96, если высота цилиндра равна половине высоты конуса