Презентация на тему: Задания с параметрами

Примеры оформления задания II части ЕГЭ по математике Задания с параметрами

ЗНАНИЕ И ТОЛЬКО ЗНАНИЕ ДЕЛАЕТ ЧЕЛОВЕКА ПОНАСТОЯЩЕМУ СИЛЬНЫМ И СВОБОДНЫМ…

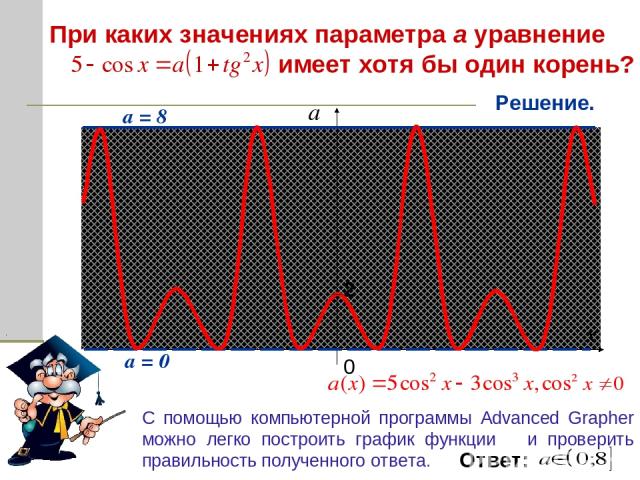
С помощью компьютерной программы Advanced Grapher можно легко построить график функции и проверить правильность полученного ответа. При каких значениях параметра а уравнение имеет хотя бы один корень? Запишем данное уравнение в виде: Исследуем функцию a (t) с помощью производной : Значения функции на концах: график исходной функции располагается в полосе (0;8], значит исходное уравнение имеет хотя бы одно решение при Решение. . . Почему? Почему?

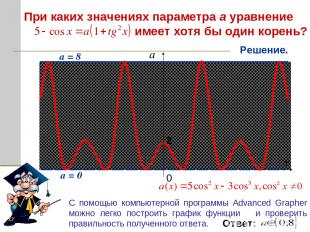
С помощью компьютерной программы Advanced Grapher можно легко построить график функции и проверить правильность полученного ответа. При каких значениях параметра а уравнение имеет хотя бы один корень? Решение. а = 8 а = 0

Решите задачи, по предложенной схеме Пример 1. При каких значениях параметра а уравнение не имеет корней? Пример 2. При каких значениях параметра а уравнение имеет хотя бы один корень? С помощью компьютерной программы Advanced Grapher можно легко построить график функции и проверить правильность полученного ответа.

Найти все значения параметра а, при каждом из которых система уравнений а((х²)²+1) = у+2-|х|, х ² +у ² =4 имеет единственное решение.

Решение: Если пара чисел (х,у) является решением системы, то учитывая четность степени переменной х и присутствие знака модуля сделаем вывод, что пара (-х, у) тоже является решением системы. По условию задачи система должна иметь одно решение, значит, х = - х = 0. Получаем пару (0, у).

1.Тогда система упростится и первое уравнение примет вид а=у+2, а второе уравнение: у ² =4. Откуда у= ±2, а=о или 4. 2. При а=0 исходные уравнения приводятся к 0=у+2-|х| и х ² +у ² =4. Система из данных уравнений будет иметь как минимум два решения: х= ±2, у=0.

3. При а=4 система принимает вид 4((х²)²+1) = у+2-|х|, у=4х + |х|+2 х= 0 х ² +у ² =4 у ² =4 - х ² у=2 Таким образом, при а=4 исходная система имеет одно единственное решение. Ответ: 4.

Найдите значения параметра  а, при каждом из которых уравнение имеет единственное решение.

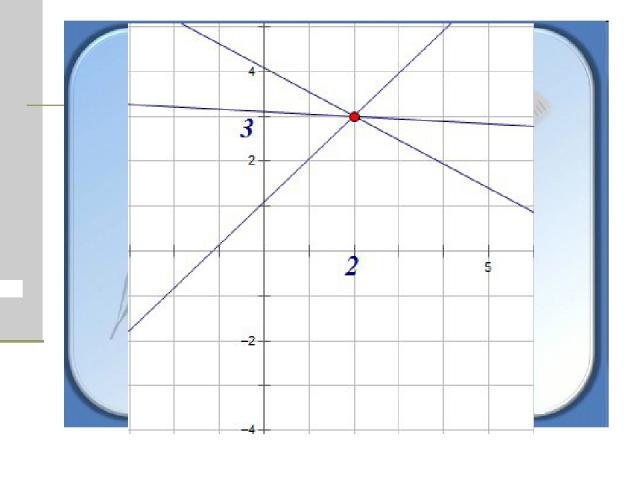
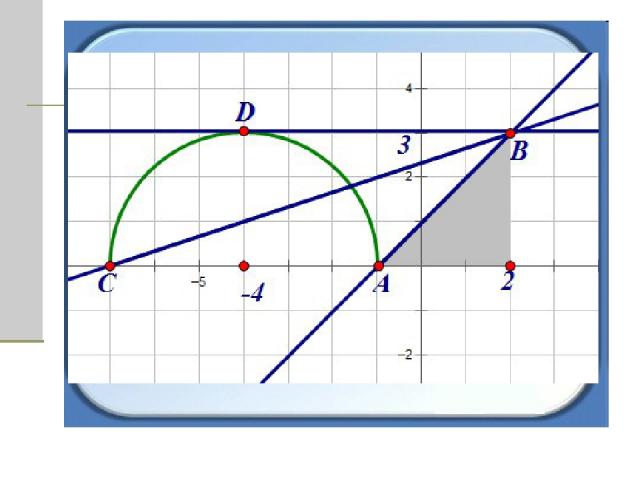
Решим задачу графическим способом Первая функция: у = 2а- ах +3 и вторая функция у = . График первой функции представляет из себя семейство прямых,  которые имеют различный коэффициент наклона  и общую точку с координатами (2; 3).

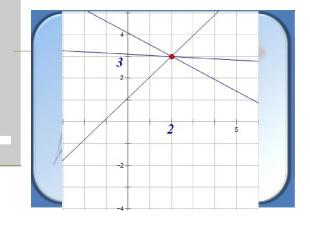
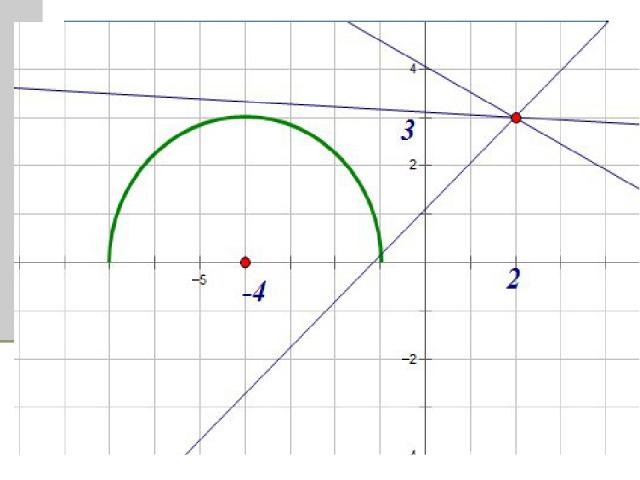
Вторая функция:  Преобразуем выражение под корнем – выделим полный квадрат: График функции   представляет из себя полуокружность с центром в точке (-4;0) и радиусом 3.

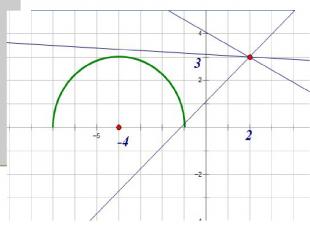
Вторая функция: Преобразуем выражение под корнем – выделим полный квадрат:

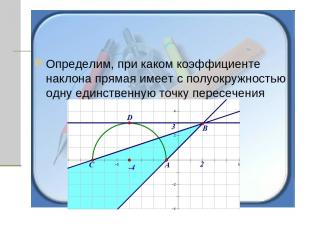
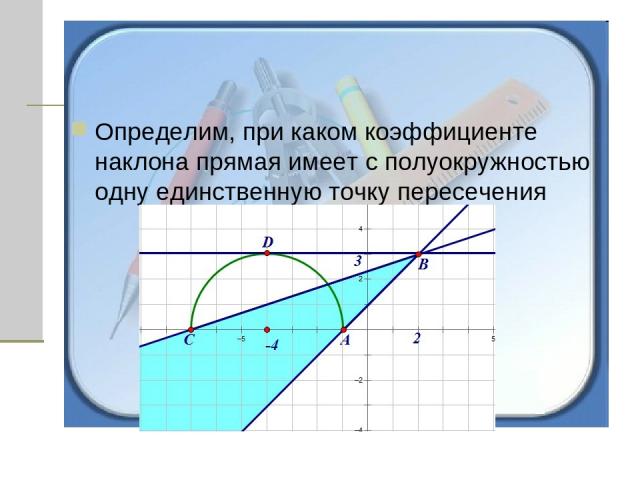
Определим, при каком коэффициенте наклона прямая имеет с полуокружностью одну единственную точку пересечения

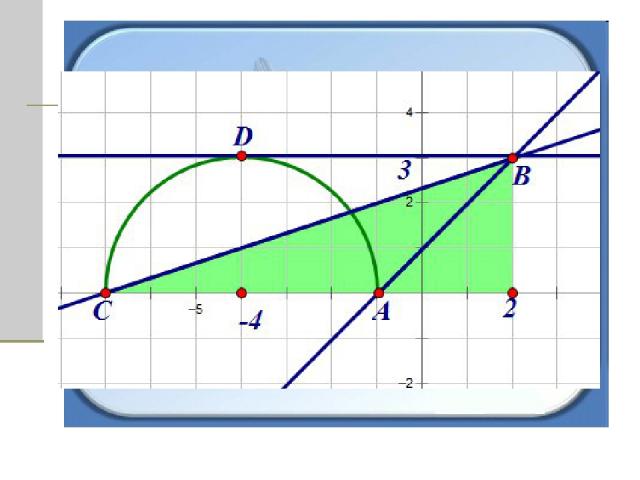
Очевидно, что прямые. Заключенные между прямыми АВ и СВ имеют с полуокружностью одну или две общие точки. Прямые АВ и DВ имеют одну общую точку, а прямая СВ имеет две общие точки. Найдем коэффициенты наклона этих прямых.

:

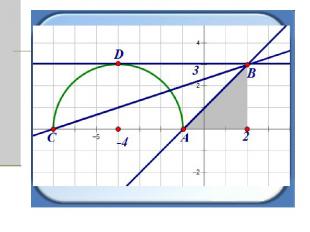
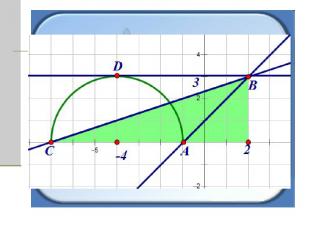
Коэффициент наклона прямой АВ равен 3/3 = 1, а коэффициент наклона прямой СВ равен 3/9 = 1/3. Коэффициент наклона прямой DВ равен 0, так как прямая DВ параллельна прямой СА.

Итак, прямая и полуокружность имеют одну общую точку, если 1/3 < - а ≤ 1 и а=0. Умножим первое неравенство на -1 и получим - 1 ≤ а < - 1/3, а=0. Ответ: - 1 ≤ а < - 1/3  , а=0.

Ф.Честерфилд «Любой человек средних способностей может надлежащею работой над собой, усердием, вниманием и упорством сделаться всем, чем захочет…»