Презентация на тему: Решение заданий С2 ЕГЭ-2010

Решение заданий С2 ЕГЭ-2010 Предмет: геометрияУчитель: Уланова М.В.Выполнила: Мокшина О., 11 Б

Задача №1: В прямоугольной системе координат заданы точки O(0;0), D(-5;0), C(0;-12). Найдите площадь боковой поверхности конуса, полученного вращением треугольника DOC вокруг стороны ОD.

Дано:O(0;0)D(-5;0)C(0;-12)Найти:Sбок. конуса-?Решение:Треугольник вращается вокруг оси ОД ► ОД – высота пирамиды, ОС – радиус.Sбок. = πR √R²+һ²= π*12 *√144+25= π*12 *√169 = π*12 *13 = 156π Ответ: Sбок. = 156π

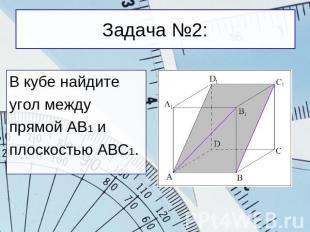
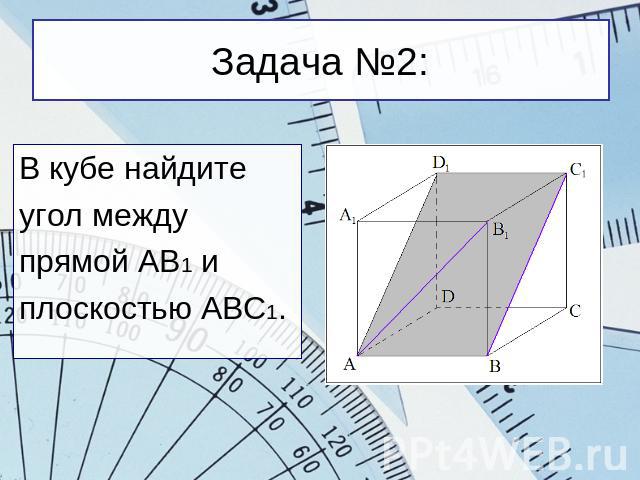
Задача №2: В кубе найдитеугол междупрямой АВ1 иплоскостью АВС1.

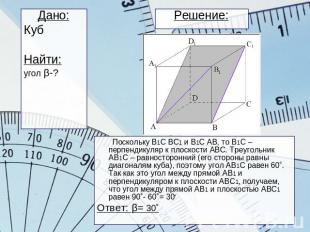
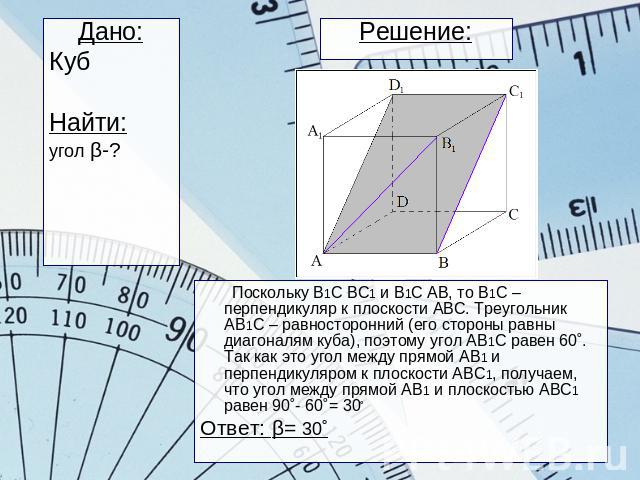
Решение: Дано:КубНайти:угол β-? Поскольку В1С ВС1 и В1С АВ, то В1С – перпендикуляр к плоскости АВС. Треугольник АВ1С – равносторонний (его стороны равны диагоналям куба), поэтому угол АВ1С равен 60˚. Так как это угол между прямой АВ1 и перпендикуляром к плоскости АВС1, получаем, что угол между прямой АВ1 и плоскостью АВС1 равен 90˚- 60˚= 30˚Ответ: β= 30˚

Задача №3: В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1, найдите косинус угла φ между плоскостями ABC и BCS.

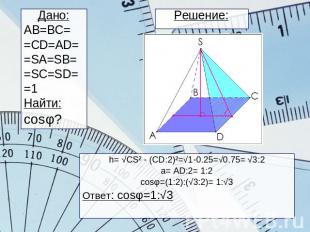
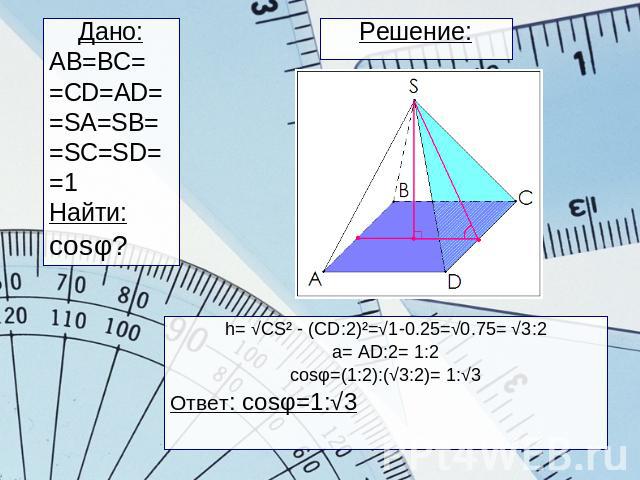
Решение: Дано:AB=BC==CD=AD==SA=SB==SC=SD==1Найти:сosφ?h= √CS² - (CD:2)²=√1-0.25=√0.75= √3:2a= AD:2= 1:2cosφ=(1:2):(√3:2)= 1:√3Ответ: cosφ=1:√3

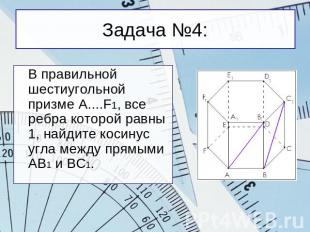
Задача №4: В правильной шестиугольной призме A....F1, все ребра которой равны 1, найдите косинус угла между прямыми АВ1 и ВС1.

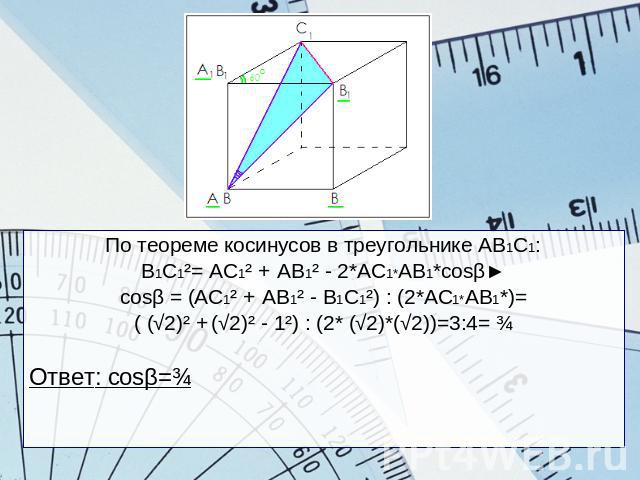
Решение: Дано:все рёбрапрямойправильнойшестиугольнойпризмы = 1Найти:сosβ-?АА1В1В и В1С1СВ – грани призмы, причем квадраты, где АВ1 и ВС1 - диагонали►АВ1=ВС1= √1² + 1²=√2По теореме косинусов в треугольнике А1В1С1:В1С1= √В1С1² + А1В1² - 2*В1С1*А1В1*cos60˚=√ 1² + 1² - 2*1*1*0,5= √2 – 1 = 1

По теореме косинусов в треугольнике АВ1С1:В1С1²= АС1² + АВ1² - 2*АС1*АВ1*cosβ►сosβ = (АС1² + АВ1² - В1С1²) : (2*АС1*АВ1*)=( (√2)² + (√2)² - 1²) : (2* (√2)*(√2))=3:4= ¾Ответ: сosβ=¾

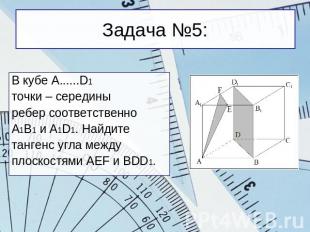
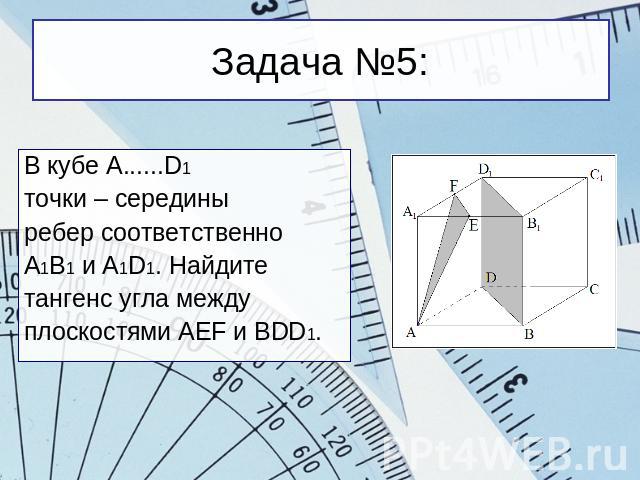
Задача №5: В кубе A......D1точки – серединыребер соответственноА1В1 и A1D1. Найдитетангенс угла междуплоскостями AEF и BDD1.

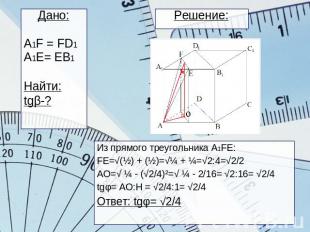
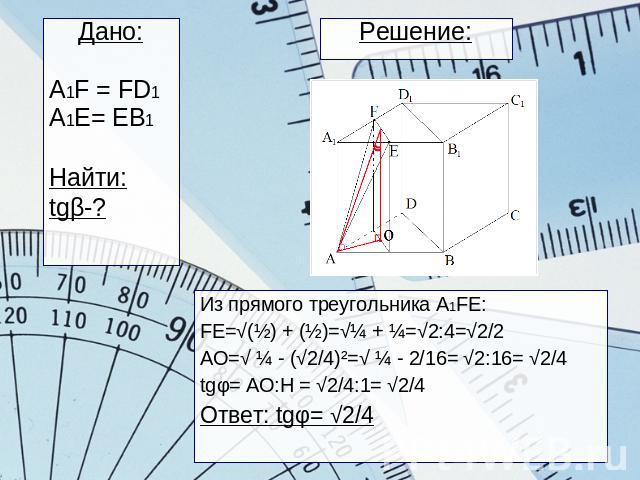
Решение: Дано:A1F = FD1A1E= EB1Найти:tgβ-?Из прямого треугольника A1FE:FE=√(½) + (½)=√¼ + ¼=√2:4=√2/2AO=√ ¼ - (√2/4)²=√ ¼ - 2/16= √2:16= √2/4tgφ= AO:H = √2/4:1= √2/4Ответ: tgφ= √2/4

Задача №6: Плоскость сечения делит диаметрсферы на части, длины которыхравны 6 и 12. Найдите отношениеменьшей части шара к большей.

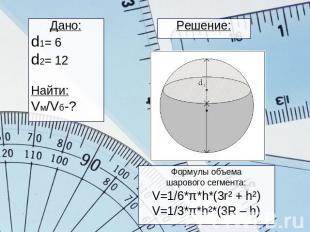
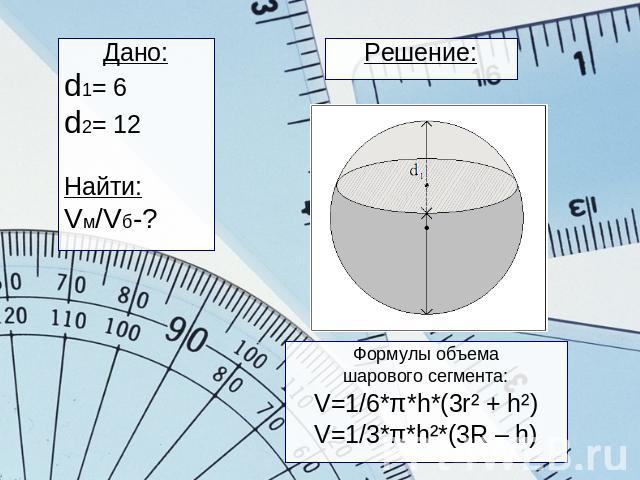
Решение: Дано:d1= 6d2= 12Найти:Vм/Vб-?Формулы объемашарового сегмента:V=1/6*π*h*(3r² + h²)V=1/3*π*h²*(3R – h)

R=(d1+d2):2=(6+12):2=18:2=9r =√R²-(R-d1)²=√9²-3²=√72=6√2Vм=1/6*π*h*(3r² + h²) =1/6*π*6*(3*72 + 36)=252πVм=1/3*π*h²*(3R - h)=1/3*π*36* *(3*9 -6)= 12*π*21= =252πVшара=4/3πR³= 4/3π*729= 972πVб= Vшара – Vм = 972π - 252π= 720πVм /Vб= 252π:720π= 7:20Ответ: Vм /Vб= 7:20