Презентация на тему: Призма. Сечения призмы

ПРИЗМА.Сечения призмы.Автор: Самохвалова Т.М

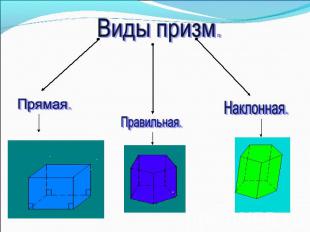
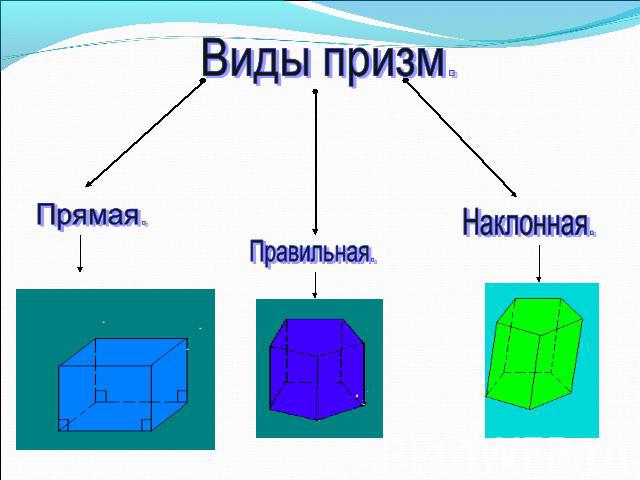
Виды призм.Прямая.Правильная.Наклонная.

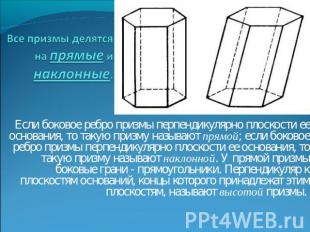
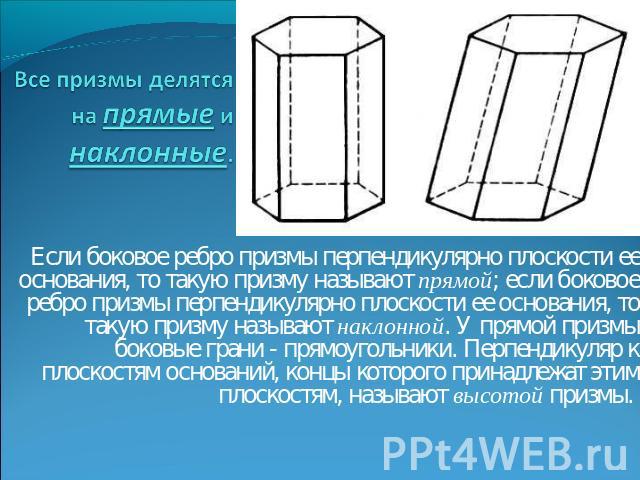
Все призмы делятся на прямые и наклонные. Если боковое ребро призмы перпендикулярно плоскости ее основания, то такую призму называют прямой; если боковое ребро призмы перпендикулярно плоскости ее основания, то такую призму называют наклонной. У прямой призмы боковые грани - прямоугольники. Перпендикуляр к плоскостям оснований, концы которого принадлежат этим плоскостям, называют высотой призмы.

Свойства призмы. 1. Основания призмы являются равными многоугольниками.2. Боковые грани призмы являются параллелограммами.3о. Боковые ребра призмы равны.

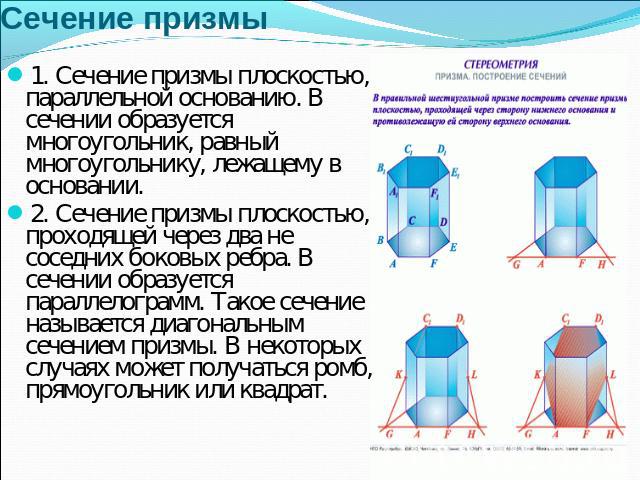
Сечение призмы 1. Сечение призмы плоскостью, параллельной основанию. В сечении образуется многоугольник, равный многоугольнику, лежащему в основании.2. Сечение призмы плоскостью, проходящей через два не соседних боковых ребра. В сечении образуется параллелограмм. Такое сечение называется диагональным сечением призмы. В некоторых случаях может получаться ромб, прямоугольник или квадрат.

Наиболее доступными и эффективными методами построения сечения призмы являются три метода:1. Метод следов.2. Метод вспомогательных сечений.3. Комбинированный метод.

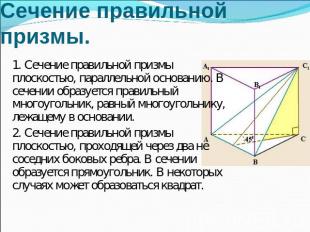
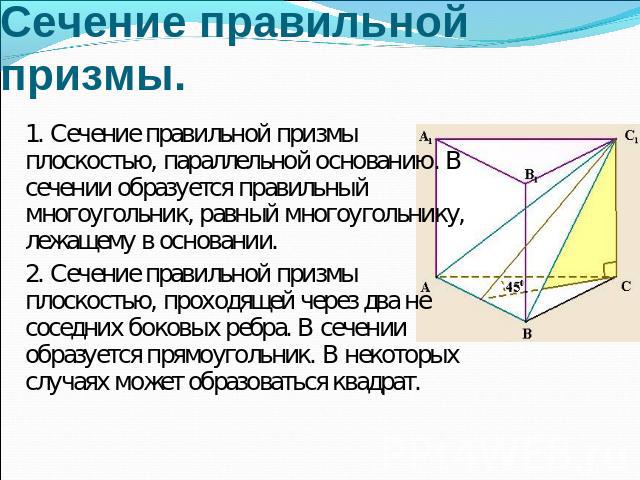
Сечение правильной призмы. 1. Сечение правильной призмы плоскостью, параллельной основанию. В сечении образуется правильный многоугольник, равный многоугольнику, лежащему в основании. 2. Сечение правильной призмы плоскостью, проходящей через два не соседних боковых ребра. В сечении образуется прямоугольник. В некоторых случаях может образоваться квадрат.

Задача. Дано: Сторона основания правильной треугольной призмы равна 8 см, боковое ребро - 6 см. Найдите Sсеч, проходящего через сторону верхнего основания и противолежащую вершину нижнего основания.Решение: Треугольник A1B1C1 - равнобедренный(A1B=C1B как диагональ равных граней)1)Рассмотрим треугольник BCC1– прямоугольныйBC12=BС2+CC12BC1= √ 64+36=10 см2) Рассмотрим треугольник BMC1– прямоугольныйBC12=BM2+MC12BM2=BC12-MC12BM2=100-16=84BM= √ 84=2 √ 21 см3) Sсеч=12 A1C1*BM= 12*2√ 21 см*8=8 √ 21

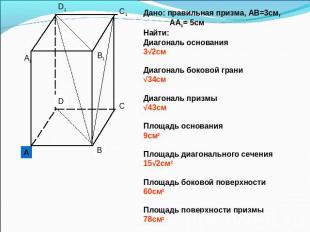
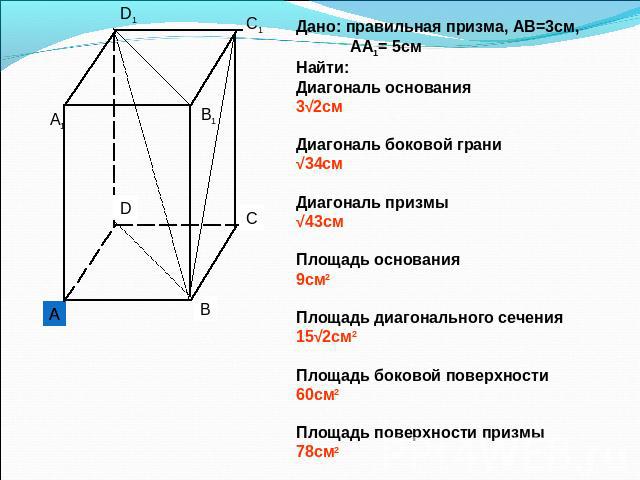
Дано: правильная призма, АВ=3см, АА1= 5смНайти: Диагональ основания3√2смДиагональ боковой грани√34смДиагональ призмы√43смПлощадь основания9см2Площадь диагонального сечения15√2см2Площадь боковой поверхности60см2Площадь поверхности призмы78см2

Применение призмы в архитектуре

Применение призмы в быту.