Презентация на тему: Построение сечений тетраэдра и параллелепипеда

Урок геометрии в 10 классе Тема: Построение сечений тетраэдра и параллелепипедаСинякина Т.В.

1 блок составного урока 3х30 Коррекция знаний по теме «Построение сечений тетраэдра и параллелепипеда»

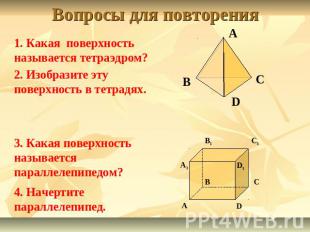
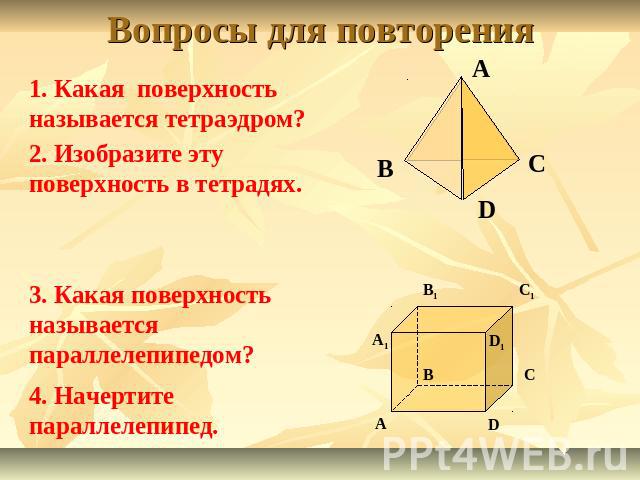
Вопросы для повторения 1. Какая поверхность называется тетраэдром?2. Изобразите эту поверхность в тетрадях.3. Какая поверхность называется параллелепипедом?4. Начертите параллелепипед.

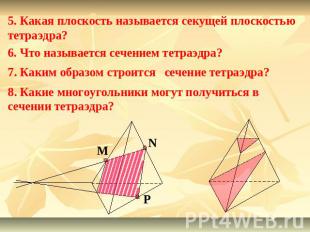
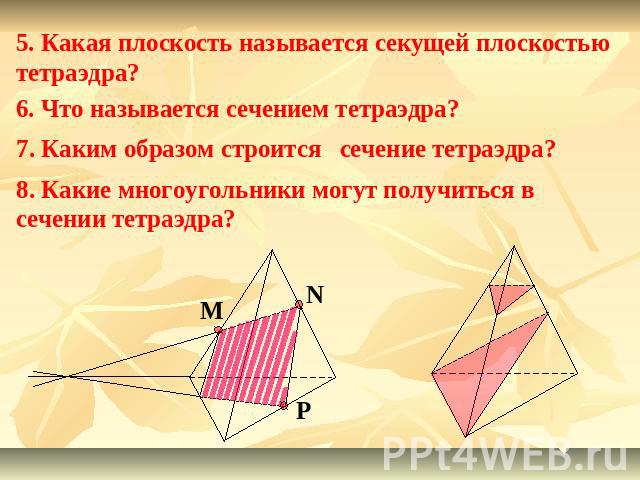
5. Какая плоскость называется секущей плоскостью тетраэдра?6. Что называется сечением тетраэдра?7. Каким образом строится сечение тетраэдра?8. Какие многоугольники могут получиться в сечении тетраэдра?

9. Какая плоскость называется секущей плоскостью параллелепипеда?10. Что называется сечением параллелепипеда?11. Какие многоугольники могут получиться в сечении параллелепипеда?12. Каким образом строится сечение параллелепипеда?

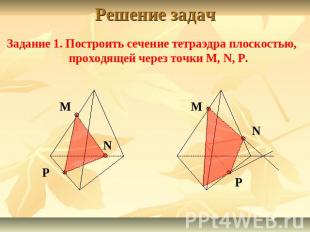
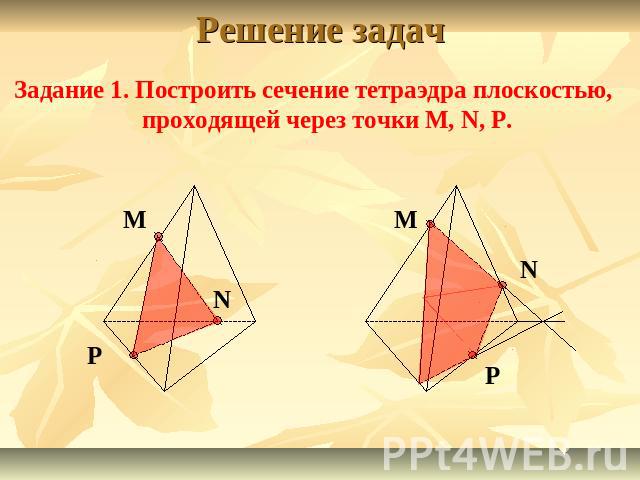
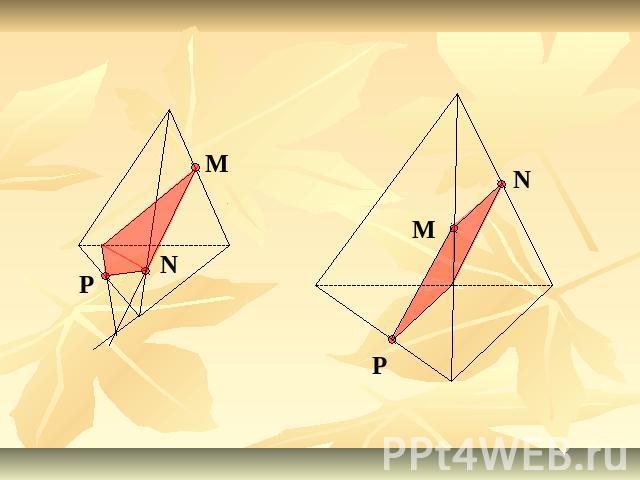
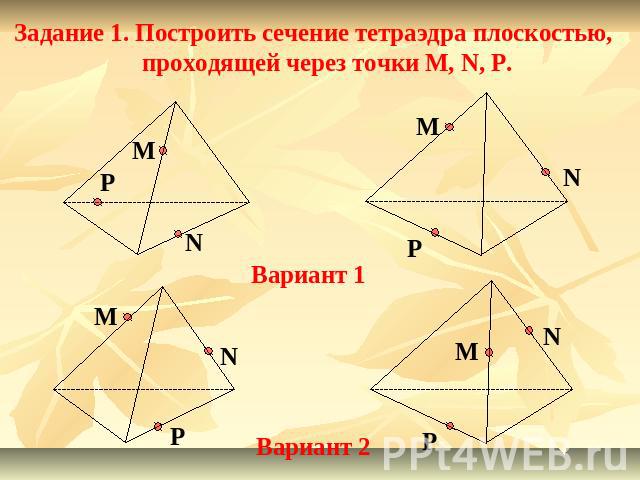
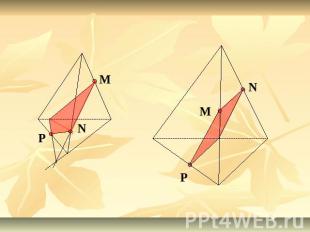
Решение задачЗадание 1. Построить сечение тетраэдра плоскостью, проходящей через точки M, N, P.

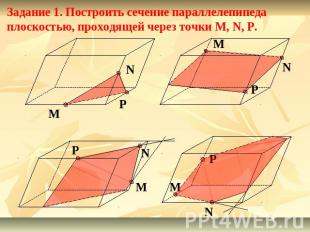
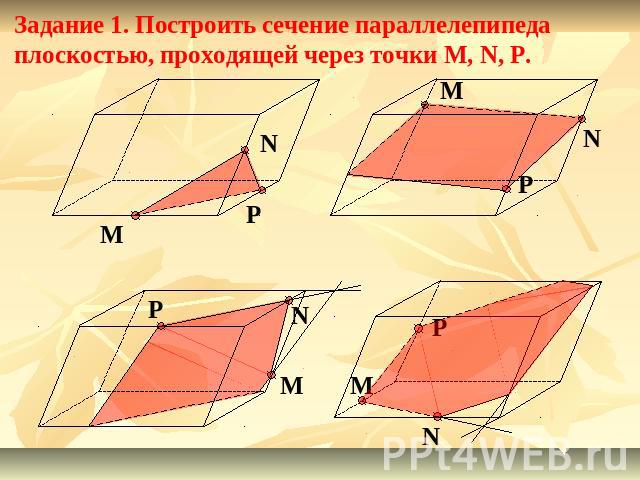
Задание 1. Построить сечение параллелепипеда плоскостью, проходящей через точки M, N, P.

2 блок составного урока 3х30 Срезовая работа по проверке умения строить сечения тетраэдра и параллелепипеда плоскостью, проходящей через три заданные точки

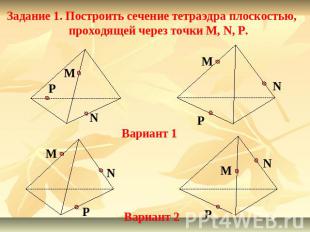
Задание 1. Построить сечение тетраэдра плоскостью, проходящей через точки M, N, P.

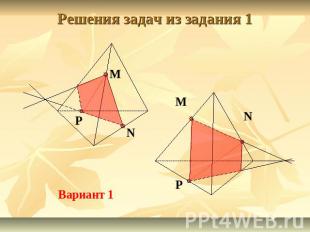
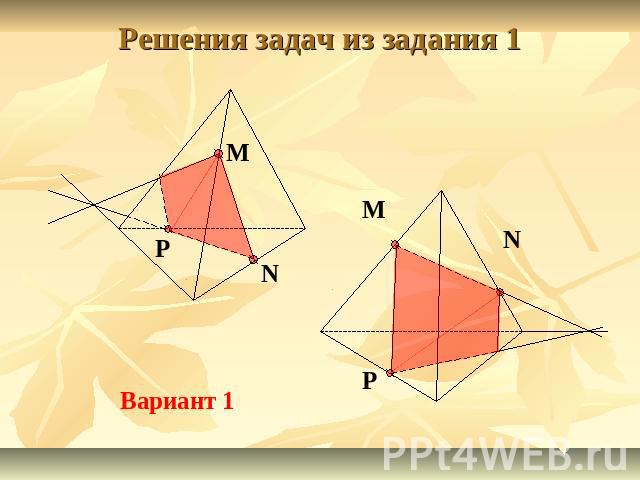
Решения задач из задания 1 Вариант 1

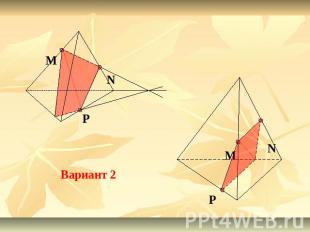
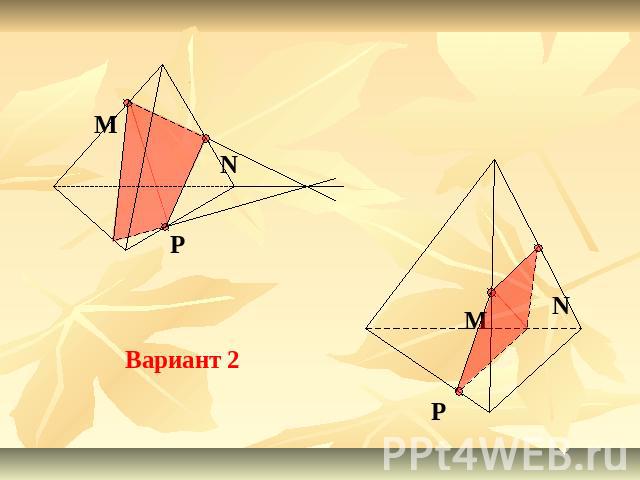
Вариант 2

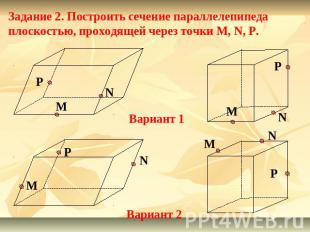
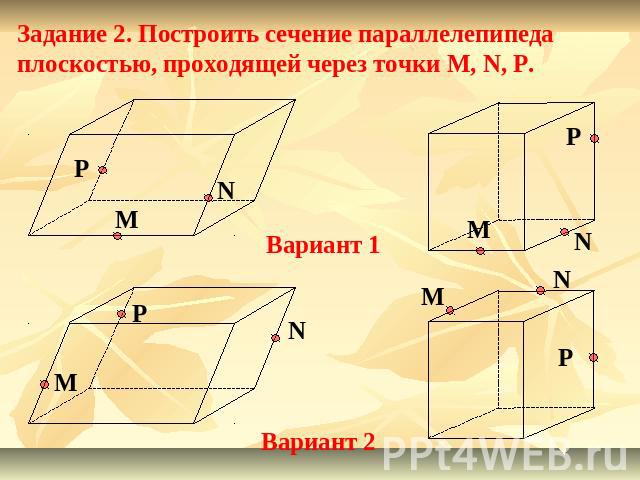
Задание 2. Построить сечение параллелепипеда плоскостью, проходящей через точки M, N, P.Вариант 1Вариант 2

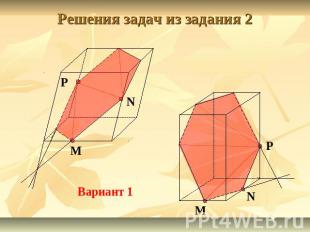
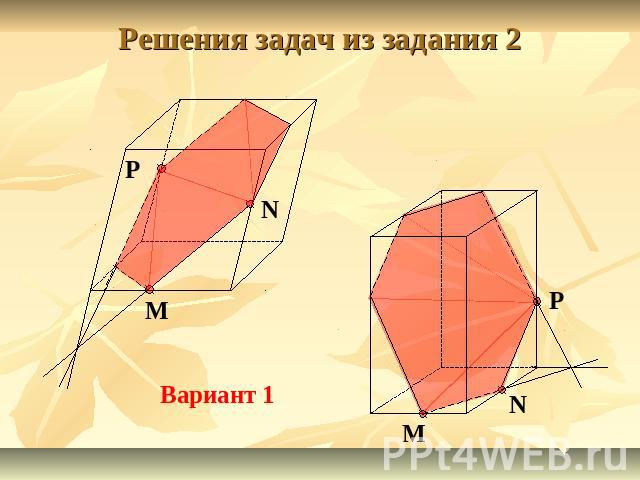
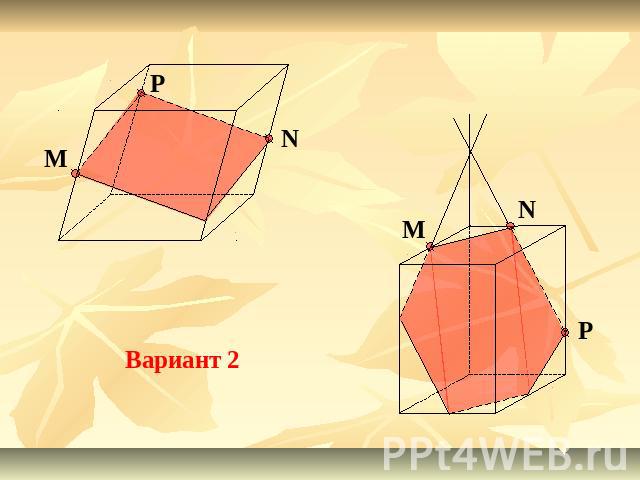
Решения задач из задания 2 Вариант 1

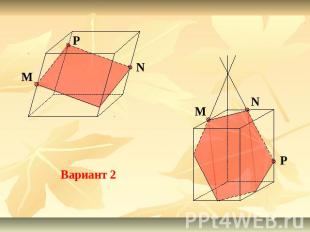
Вариант 2

3 блок составного урока 3х30 Решение сложных геометрических задач с применением навыков и умений построения сечений тетраэдра и параллелепипеда

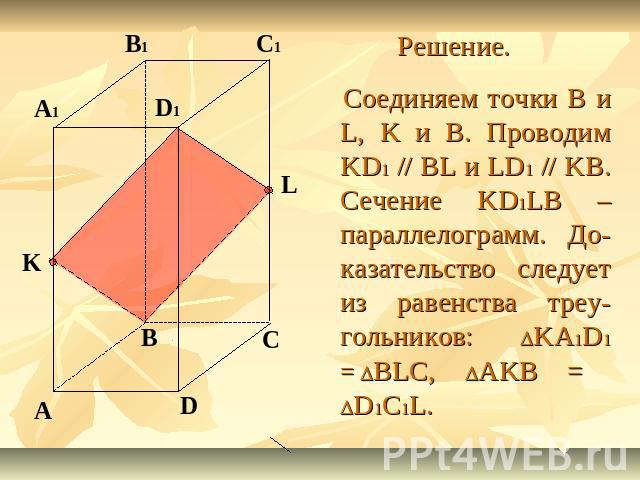
Задание 1. Построить сечение параллелепипеда ABCDA1B1C1D1 плоскостью BKL, где K – середина ребра AA1, а L – середина ребра СС1. Доказать, что построенное сечение – параллелограмм.

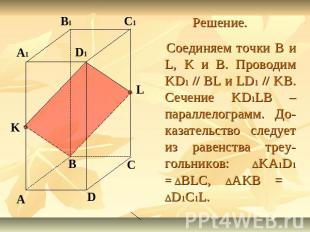
Решение. Соединяем точки B и L, K и B. Проводим KD1 // BL и LD1 // KB. Сечение KD1LB – параллелограмм. До-казательство следует из равенства треу-гольников: DKA1D1 = DBLC, DAKB = DD1C1L.

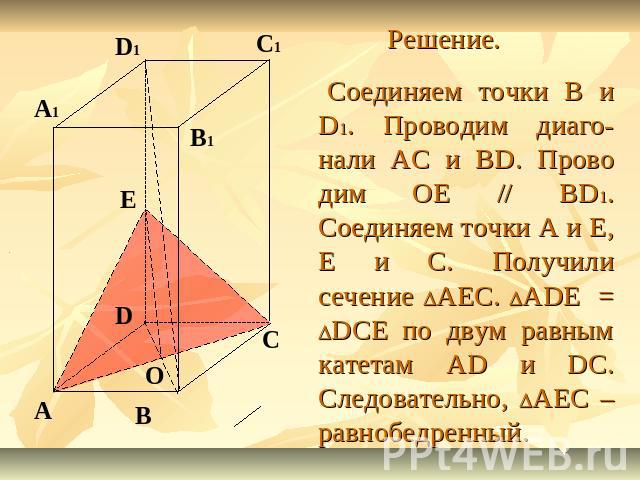
Задание 2. Построить сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через диагональ АС основания параллельно диагонали BD1. Доказать, что построенное сечение – равнобедренный треугольник, если основание параллелепипеда – ромб и углы ABB1 и CBB1 прямые.

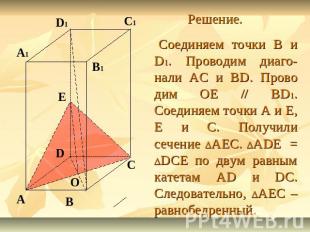
Решение. Соединяем точки B и D1. Проводим диаго-нали AC и BD. Прово дим OE // BD1. Соединяем точки А и Е, Е и С. Получили сечение DАЕС. DADE = DDCE по двум равным катетам AD и DC. Следовательно, DАЕС – равнобедренный.

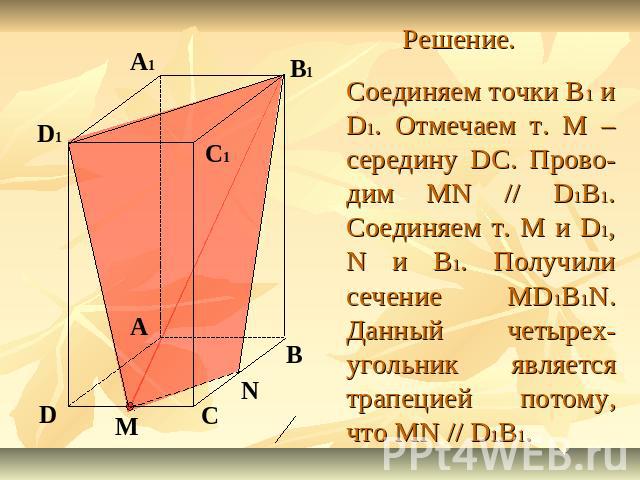
Задание 3. Построить сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через точки В1 и D1 и середину ребра CD. Доказать, что построенное сечение – трапеция.

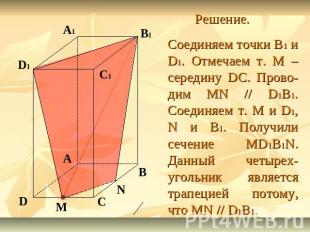
Решение. Соединяем точки B1 и D1. Отмечаем т. М – середину DC. Прово-дим MN // D1B1. Соединяем т. M и D1, N и B1. Получили сечение MD1B1N. Данный четырех-угольник является трапецией потому, что MN // D1B1.

Конец урока