Презентация на тему: Моделирование, алгоритмизация и оптимизация элементов и систем в теплоэнергетике

Северо-Западный государственный заочный технический университетКафедра теплотехники и теплоэнергетикиМоделирование, алгоритмизация и оптимизация элементов и систем в теплоэнергетике

Программа дисциплиныОбъем: 150 часовСтруктура:ВведениеГл. 1 Методологические основы математического моделированияГл. 2 Моделирование задач с использованием математическогопрограммированияГл. 3 Графическое моделированиеГл. 4 Элементы теории вероятности. Имитационное моделированиеГл. 5 Элементы теории надежностиГл. 6 Элементы математической статистикиГл. 7 Исследование математических моделейПрактические занятия:ПЗ №1 Постановка простейших математических моделей и методикаих реализации на ЭВМ.ПЗ №2 Исследование функциональных зависимостей на ЭВМ.Текущий контрольКонтрольные работы:КР №1 Построение и оптимизация сетевой моделиКР№2 Решение транспортной задачи методами математического программирования Промежуточная аттестация:Экзамен

Литература:Моделирование, алгоритмизация и оптимизация элементов и систем в теплоэнергетике /Методический комплекс. СПб, СЗТУ, 2004 (htpp://window.edu.ru/window/catalog?p_rid=24926)  2. Вентцель Е.С. Исследование операций: Задачи, принципы, методология.- М.: Высшая школа, 2001.3. Карманов В.Г. Математическое программирование: учебное пособие.- 5-е изд.- М.:Физматлит, 20044. Лисицын В. Основы методов оптимизации.- М.: МАИ, 20035 Пантелеев А.В. Методы оптимизации в примерах и задачах: учебное пособие для студентов высших технических учебных заведений. – М.: Высшая школа, 2005.6. Салмин И.Д. Математические методы решения оптимизационных задач: учебное пособие.- М.: МИФИ,2004 7. Загребаев А.М. и др. Методы математического программирования в задачах оптимизации сложных технических систем.- М.: МИФИ, 2007.

Понятие системы Система – совокупность объектов, взаимодействие которых вызывает наличие новых, интегративных качеств, не свойственных образующим систему компонентам(Афанасьев В.Г. «Философские проблемы управления»)Система (греч. — целое, составленное из частей; соединение элементов ) – организация существования явлений, процессов, вещей, элементов, обособленного целого, которую составляют находящиеся во взаимных отношениях части и элементы. (Большой толковый словарь)Система- множество взаимосвязанных объектов, организованных некоторым способом в единое целое.(Википедия – свободная энциклопедия)Система — набор сущностей и их связей, выделенных из среды на определенное время и с определенной целью.объединение или совокупность элементов, скомбинированных природой или человеком таким образом, чтобы образовать единое или составное целое (Американская энциклопедия)Система- это соединение компонентов, которые взаимодействуют друг с другом для выполнения функций, которые не могут быть исполнены никакой из отдельно взятых частей (стандартный словарь терминовIEEE по электротехнике и электронике)

Итак, система – это:-совокупность элементов (подсистем). При определенных условиях элементы сами могут рассматриваться как системы, а исследуемая система – как элемент более сложной системы;связи между элементами в системе превосходят по силе связи этих элементов с элементами, не входящими в систему. Это свойство позволяет выделить систему из среды; для любой системы характерно существование интегративных качеств (свойство эмерджентности), которые присущи системе в целом, но не свойственны ни одному ее элементу в отдельности: систему нельзя сводить к простой совокупности элементов;система всегда имеет цели, для которых она функционирует и существует

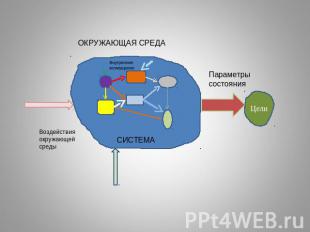
Основными понятиями общей теории систем являются «целостность», «структура», «элемент», «связи», «функции», «цели», «среда» и т.д.Целостность — несводимость свойств целого к его составляющим, анализ частей системы с точки зрения целого.Структура — расположенность относительно друг друга входящих в систему элементов и частей.Элемент — составляющая часть системы, наделённая в системе определенными функциями.Подсистема — часть рассматриваемой системы; относительно самостоятельная и оформленная система, действующая как часть целого.Целью системы является сохранение и воспроизводство самой системы, а также взаимодействие с другими системами — внешними и внутренними.Цели – это те конечные результаты, на достижение которых направлена деятельность

Классификация системВиды систем — совокупность определённых признаков, позволяющих соотносить рассматриваемую систему с той или иной группой. Прежде всего необходимо определить способ выделения системообразующего критерия (совокупности таких критериев) и классификации систем по данному критерию (совокупности критериев).А. По предметной областиЭкологическая система - это весь материальный мир обитания человекаФизические системы обеспечивают различные взаимодействия тел и полей Химические системы осуществляют непрерывный обмен веществ в природе, их преобразованиеБиологические системы координируют жизнедеятельность всех организмов и их отдельных органовСоциальные системы - это идеально-реальный мир, в котором живет человек (общество, государство, семья, …)Искусственные системы - это системы, созданные человеком в результате направленной деятельности

Классификация системБ. По свойствамДинамические (статические) - выход (не) зависит от предысторииДетерминированные (стохастичные) - есть (нет) повторяемость нет (есть) случайности Линейные (нелинейные) Стационарные (нестационарные) - нет (есть) изменения параметров во времениДискретные (непрерывные) - выход системы изменяется во времени дискретно, через шаг t (непрерывно) В. По сложности и размерамСложные – членение системы на компоненты разных уровней происходит до компонент, которые остаются системами со всеми характерными свойствами систем.Простые –компоненты систем не являются системамиБольшие – сложные многоуровневые (иерархические) системы, в которых пространственный фактор имеет существенное значениеГ. По степени участия человекаТехнические (без участия человека, в том числе САУ)Организационные (коллективы людей, образованные с определенными целями)Человеко-машинные

Системный подход – направление научного познания и социальной практики, в основе которого лежит рассмотрение объектов как систем; ориентирует исследование на раскрытие целостности объекта, на выявление многообразных типов связей в нем и сведение их в единую теоретическую картинуМетодология системного подхода при решении задач анализа систем сводится к тому, что исследования объекта ориентируются на раскрытие его интегративных качеств, на выявлении многообразных связей и механизмов, обеспечивающих эти качества. Методология системного подхода при решении задач проектирования и синтеза систем состоит в следующем. Задача проектирования системы расчленяется на подзадачи проектирования ее элементов. Причем, каждый из элементов должен рассматриваться не сам по себе, а во взаимодействии с другими элементами. Решение подзадач должно происходить при условии обеспечения интегративных качеств функционирования всей системы.

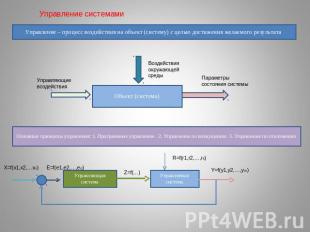
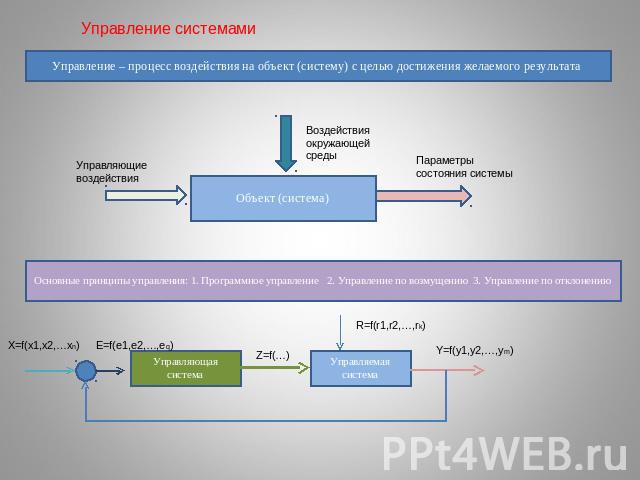
Управление системамиУправление – процесс воздействия на объект (систему) с целью достижения желаемого результата Основные принципы управления: 1. Программное управление 2. Управление по возмущению 3. Управление по отклонению

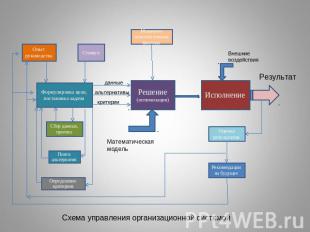
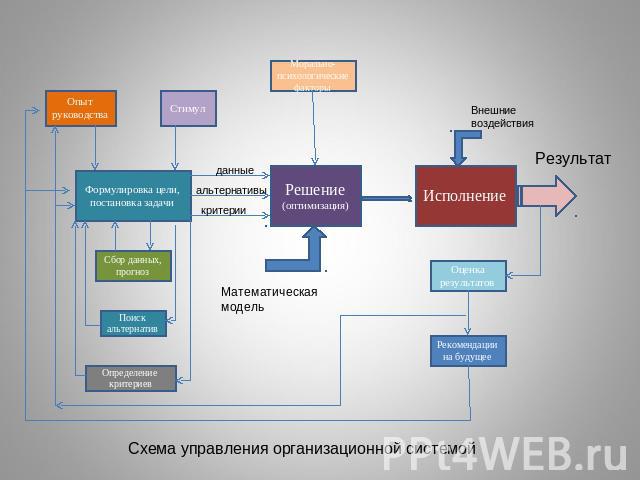
Схема управления организационной системой

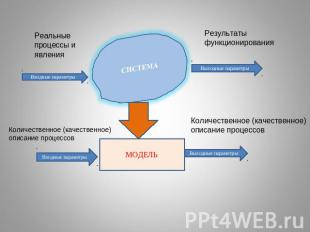
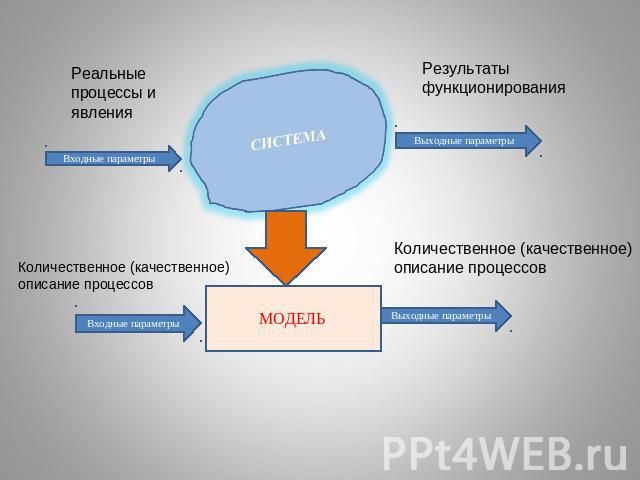
Что такое модель?Модель (французское modele, от латинского modulus - мера, образец)Модель — в конструировании, промышленном дизайне — изделие или деталь изделия которое воспроизводит форму и/или другие характеристики сложного иделия или детали. Модель, как правило, намного дешевле и быстрее в изготовлении, чем моделируемое изделие. Используется для уточнения характеристик изделия или детали. (Википедия)Модель — Устройство, воспроизводящее, имитирующее строение и действие какого-либо другого («моделируемого») устройства в научных, образовательных, производственных (при испытаниях) или спортивных целях (Википедия)Модель — любой образ, аналог (мысленный или условный: изображение, описание, схема, чертеж, график, карта и т.п.) какого-либо объекта, процесса или явления («оригинала» данной модели) (Википедия)Модель — упрощенное представление некоторого объекта или явления. Модель содержит в себе те характеристики и свойства, которые имеют отношение к решаемой задаче Модель дает упрощенное описание объекта или явленияМодель соответствует реальному объекту или явлению Модель создается для решения некоторой задачи

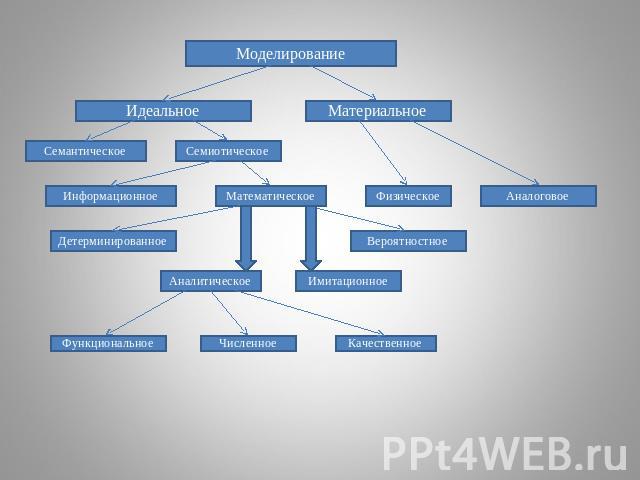
Моделирование - одна из основных категорий теории познания: на идее моделирования, по существу, базируется любой метод научного исследования как теоретической (при котором используются различного рода знаковые, абстрактные модели), так и экспериментальный (использующий предметные модели).Моделирование – это исследование каких-либо явлений, процессов или систем объектов путем построения и изучения их моделей; использование моделей для определения или уточнения характеристик и рационализации способов построения вновь конструируемых объектов. Формы представления моделей:Уменьшенные (увеличенные) копии объектовФизические (химические, биологические, социальные, …) аналогии с объектом;Словесные описания;Чертежи и блок-схемы;Логические блок-схемы и таблицы решений;Кривые, таблицы и номограммы;Математические описания(ЛИ Т.Г., Адамс Г.Э., Гейнз У.Н. «Управление процессами с помощью ЭВМ, моделирование и оптимизация)

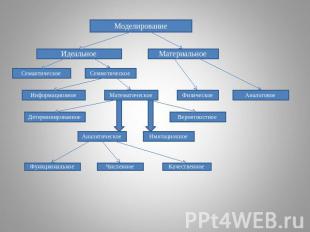
Математическое моделирование — процесс построения и изучения математических моделей реальных процессов и явлений. Математической моделью реальной системы называется совокупность соотношений (формул, уравнений, неравенств, логических условий, операторов и т.д.), определяющих характеристики состояний системы (а через них и выходные сигналы) в зависимости от параметров системы, входных сигналов, начальных условий и времени(Бусленко Н.П. «Моделирование сложных систем)Математическая модель — это упрощенное описание реальности с помощью математических понятий. Все естественные и общественные науки, использующие математический аппарат, по сути занимаются математическим моделированием: заменяют реальный объект его моделью и затем изучают последнюю. Как и в случае любого моделирования, математическая модель не описывает полностью изучаемое явление, и вопросы о применимости полученных таким образом результатов являются весьма содержательными.

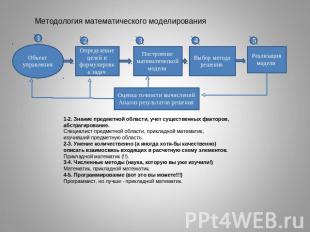
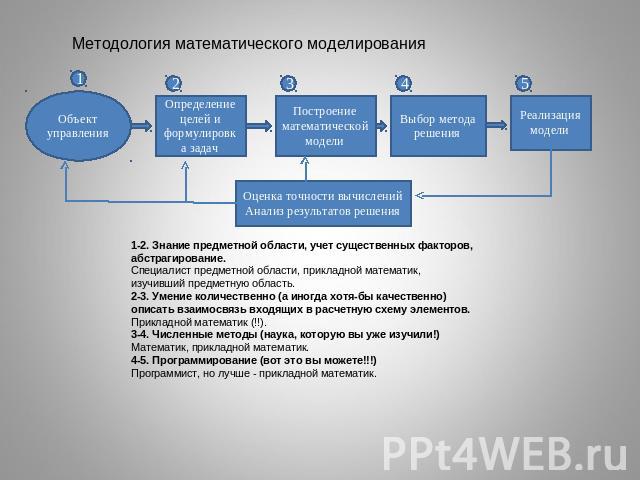
Методология математического моделирования1-2. Знание предметной области, учет существенных факторов, абстрагирование.Специалист предметной области, прикладной математик, изучивший предметную область.2-3. Умение количественно (а иногда хотя-бы качественно) описать взаимосвязь входящих в расчетную схему элементов.Прикладной математик (!!).3-4. Численные методы (наука, которую вы уже изучили!)Математик, прикладной математик.4-5. Программирование (вот это вы можете!!!)Программист, но лучше - прикладной математик.

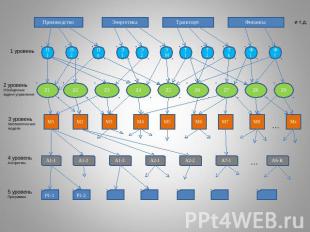
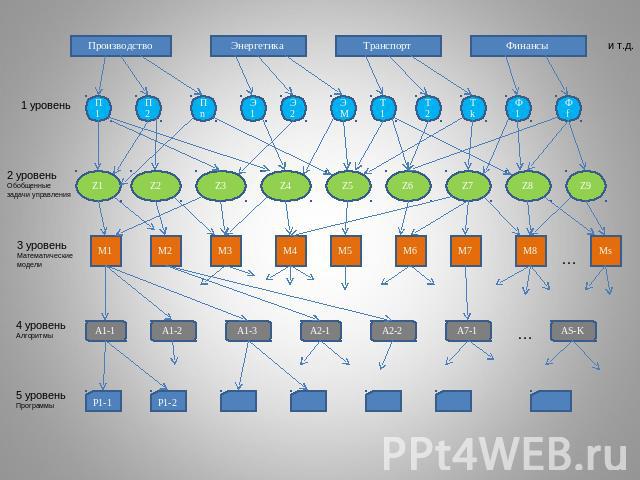
2 уровень - Обобщенные задачи управления

3 уровень – математические модели

Обобщенные задачи управления и методы их решенияZ1. Задачи автоматического управленияМетоды решения:М1 – Дифференциальные и разностные уравненияМ2 – Теория автоматов и математическая логикаZ2. Задачи распределения и назначенияМетоды решения:М1 - Дифференциальные и разностные уравненияМ4 – Линейное программированиеМ5 – Нелинейное программированиеМ6 – Динамическое программированиеМ7 – Динамическое программированиеМ8 – Стохастическое программированиеМ10 – Теория расписаний и комбинаторная математикаМ12 – Теория графов и сетейМ14 – Теория семиотики

Обобщенные задачи управления и методы их решенияZ3. Задачи управления запасамиМетоды решения:М1 - Дифференциальные и разностные уравненияМ8 – Стохастическое программированиеМ12 – Теория графов и сетейZ4. Задачи надежности и замены оборудованияМетоды решения:М1 - Дифференциальные и разностные уравненияМ7 – Динамическое программированиеМ13 - Теория массового обслуживания и Марковские процессыZ5. Задачи массового обслуживанияМетоды решения:М1 - Дифференциальные и разностные уравненияМ10 – Теория расписаний и комбинаторная математикаМ12 – Теория графов и сетейМ13 - Теория массового обслуживания и Марковские процессы

Обобщенные задачи управления и методы их решенияZ6. Задачи упорядочения и согласованияМетоды решения:М2 - Теория автоматов и математическая логикаМ6 – Дискретное программированиеМ10 – Теория расписаний и комбинаторная математикаМ12 – Теория графов и сетейМ14 – Теория семиотикиZ7. Задачи поиска и диагностикиМетоды решения:М2 - Теория автоматов и математическая логикаМ4 – Линейное программированиеМ5 – Нелинейное программированиеМ9 - Теория распознаванияZ8. Задачи сетей и выбора маршрутовМетоды решения:М4 – Линейное программированиеМ7 – Динамическое программированиеМ10 – Теория расписаний и комбинаторная математикаМ12 – Теория графов и сетей

Обобщенные задачи управления и методы их решенияМетоды решения:М2 - Теория автоматов и математическая логикаМ4 – Линейное программированиеМ8 – Стохастическое программированиеМ11 - Теория игр и статистических решений

Системы, описываемые дифференциальными уравнениями

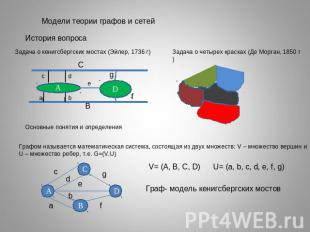
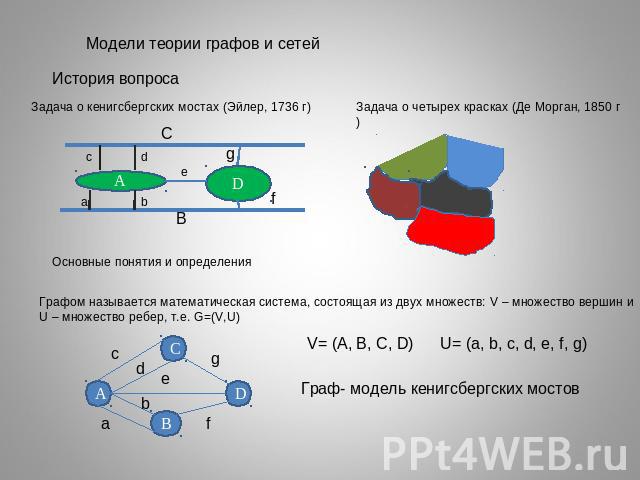
Модели теории графов и сетейГрафом называется математическая система, состоящая из двух множеств: V – множество вершин иU – множество ребер, т.е. G=(V,U)

Основные понятия и определенияГрафы бывают ориентированными, неориентированными и смешаннымиГраф – множество элементов (V, U), между которыми установлено отношение инцидентности

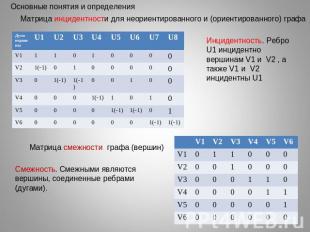
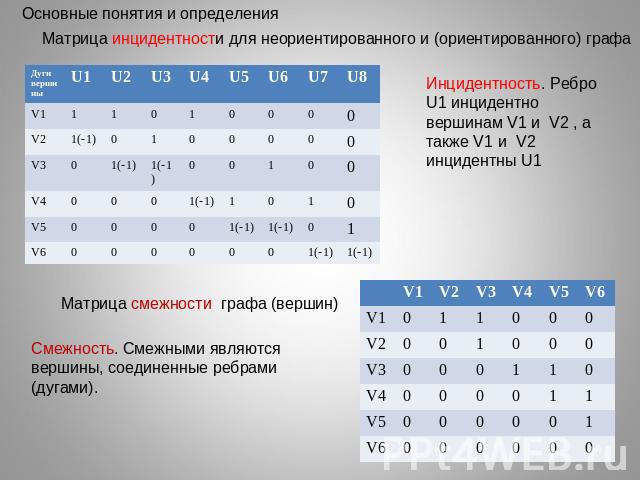
Основные понятия и определенияМатрица инцидентности для неориентированного и (ориентированного) графаИнцидентность. Ребро U1 инцидентно вершинам V1 и V2 , а также V1 и V2 инцидентны U1Матрица смежности графа (вершин)Смежность. Смежными являются вершины, соединенные ребрами (дугами).

Основные понятия и определенияИзоморфность. Графы, у которых вершины и ребра (или дуги) могут быть поставлены во взаимно однозначное соответствие таким образом, что соотношения инцидентности у них одинаковые, называются изоморфнымиЧасть графа. Граф H называется частью графа G, H ϵ G,если множество его вершин V(H) содержится в множестве V(G), амножество его ребер U(H) – в множестве U(G). H(V1,V2,V3,V5) – часть графа G Суграф. Если V(H) = V(G), часть графа называется суграфомПодграфом F(S) графа G(V) с множеством вершин S ϵ V называется часть, которой принадлежат все ребра с обоими концами из SСтепень вершины графа – это количество ребер, инцидентных данной вершине

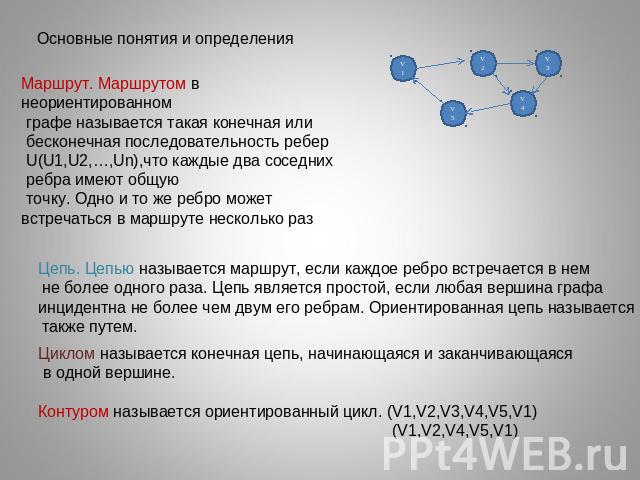
Основные понятия и определенияМаршрут. Маршрутом в неориентированном графе называется такая конечная или бесконечная последовательность ребер U(U1,U2,…,Un),что каждые два соседних ребра имеют общую точку. Одно и то же ребро можетвстречаться в маршруте несколько разЦепь. Цепью называется маршрут, если каждое ребро встречается в нем не более одного раза. Цепь является простой, если любая вершина графа инцидентна не более чем двум его ребрам. Ориентированная цепь называется также путем.Циклом называется конечная цепь, начинающаяся и заканчивающаяся в одной вершине.Контуром называется ориентированный цикл. (V1,V2,V3,V4,V5,V1) (V1,V2,V4,V5,V1)

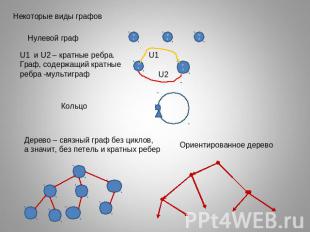
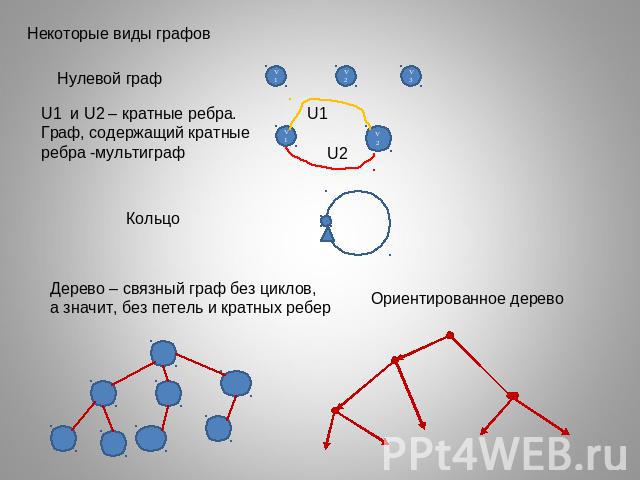
Некоторые виды графовU1 и U2 – кратные ребра. Граф, содержащий кратные ребра -мультиграфДерево – связный граф без циклов, а значит, без петель и кратных реберОриентированное дерево

Операции над графами: Объединение G1UG2 Соединение G1 + G2 Произведение G1 X G2 Композиция G= G1[ G2 ]Некоторые задачи теории графовЗадача о Кенигсбергских мостахОбходу мостов соответствует последовательность ребер графа задачи,В которой два соседних ребра имеют общую вершину, т.е. маршрут. Этот маршрут является простым циклом, содержащим все ребра графа..Такие циклы и графы называются Эйлеровыми. Его можно изобразить одним росчерком пера.Теорема Эйлера. Конечный неориентированный граф эйлеров тогда и только тогда, когда он связан и степени всех его вершин четны2. Задача о выходе из лабиринта.Может использоваться алгоритм обхода ребер графа.Более эффективен т.н. Гамильтонов цикл, т.е. цикл, проходящий через все вершины графа.Более сложные классы задач, решаемые методами теории графов:Взвешенные графыПокрытияРаскраски и т.д.