Презентация на тему: Свойства обратных тригонометрических функций

МАСТЕР-КЛАСС Элективный курс по математике, как один из важных инструментов реализации задач профильного обучения Косолапова Л.В., учитель математики МОУ СОШ им. А.С. Попова городского округа Власиха Московской области 900igr.net

Тема элективного занятия: «ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ. РЕШЕНИЕ УРАВНЕНИЙ, СОДЕРЖАЩИХ АРКФУНКЦИИ»

ЦЕЛИ УРОКА: 1. Обобщить, систематизировать и углубить знания и умения учащихся по теме «Обратные тригонометрические функции. Решение уравнений, содержащих аркфункции». 2. Прививать интерес к исследовательской деятельности и работе в группах. 3. Научить применять полученные на уроках знания в измененной ситуации, успешно справляться с задачами повышенной сложности и нестандартными задачами с целью подготовки к успешной сдаче ЕГЭ.

ПЛАН УРОКА Исследовательская работа Устные упражнения Проверка домашнего задания Решение уравнений Работа в группах Подведение итогов

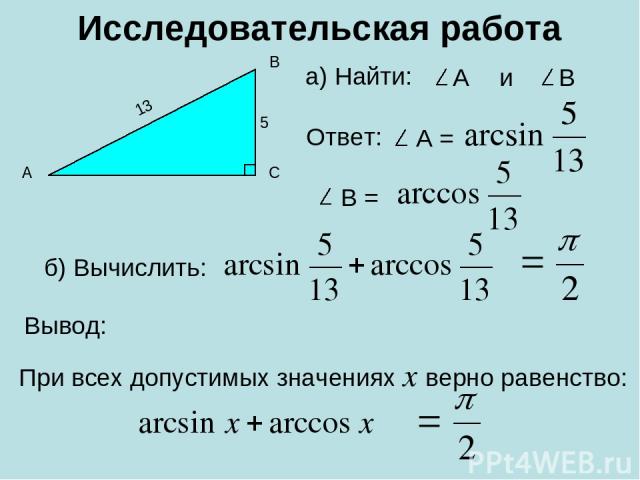
Исследовательская работа а) Найти: В А С 5 13 А В и Ответ: А = В = б) Вычислить: При всех допустимых значениях х верно равенство: Вывод:

Исследовательская работа в) Найти: В А С 5 12 А В и Ответ: А = В = г) Вычислить: Вывод:

Устные упражнения 1. Найдите значение выражения: Решение:

Устные упражнения 2. Укажите область определения функции: Решение:

Устные упражнения 3. Укажите область значений функции: Решение:

Устные упражнения 4. Найдите значение выражения: Ответ:

Устные упражнения Решение:

Устные упражнения Решение: Пусть тогда Но Значит

Устные упражнения Решение:

Устные упражнения Решение:

Проверка домашнего задания Решение. Методы решения уравнения нестандартные. Найти область допустимых значений уравнения трудно. Если уравнение имеет решение, то решениями являются тройки чисел (x0, y0, z0) и, в частности, определены выражения: и т.е. справедлива система неравенств: ,

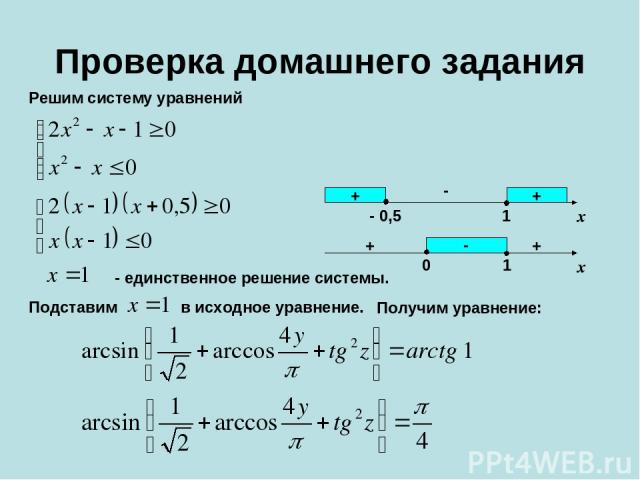
Проверка домашнего задания Решим систему уравнений Подставим + + - - 0,5 1 x + + - 0 1 x - единственное решение системы. в исходное уравнение. Получим уравнение:

Проверка домашнего задания Т.к. Оценим каждое слагаемое левой части уравнения. только для , то По определению арккосинуса . при всех допустимых значениях z. Значит, оба слагаемые неотрицательны. Сумма двух неотрицательных слагаемых равна нулю, если каждое из них равно нулю, т.е.

Проверка домашнего задания Итак, если исходное уравнение имеет решение, то все они содержатся среди троек чисел

Проверка домашнего задания Проверка показывает, что каждая такая тройка удовлетворяет исходному уравнению, а значит, является решением этого уравнения. Ответ:

Повторение


Итак, при решении уравнений, содержащих аркфункции, используются общие приемы решения уравнений. Они связаны с установлением области определения уравнения, оценкой множеств значений выражений в левой и правой частях уравнения, исследованием функций на монотонность.

Работа в группах Уравнения, содержащие аркфункции, разделяют на виды по способу их решения: уравнения, способ решения которых предполагает использование свойств аркфункций; простейшие уравнения; уравнения, сводящиеся к алгебраическим относительно аркфункции; уравнения, способ решения которых состоит в действии тригонометрической функции на обе части уравнения.

Работа в группах. Решить уравнения

Ответы к работе в группах Корней нет Корней нет 2 - 1/3 1,5 1 -7

Итоги урока Результаты групповой работы: I место – команда Григорьевой Владиславы II место – команда Горяйновой Виктории III место – команда Гридасова Виктора Ребята получили поздравления и поощрительные призы с пожеланиями дальнейших успехов в учебе.